Лабораторная работа № 9 определение частотной дисперсии стеклянной призмы с помощью гониометра

1. Классическая электронная теория дисперсии

В классической теории дисперсии оптический электрон в атоме рассматривается как затухающий дипольный осциллятор, характеризуемый определенной собственной частотой и постоянной затухания , так что в поле световой волны уравнение его движения имеет вид:

, (9.1)

где - смещение электрона от положения равновесия, - заряд электрона, - масса электрона.

Несмотря на то, что с позиции современной физики применение законов классической физики к описанию движения электронов в атоме является неоправданным, такой подход приводит к результатам аналогичным тем, которые получаются гармонического осциллятора в квантовой теории дисперсии. Сама модель дипольного осциллятора в классической теории дисперсии в свете современных представлений о строении атома, конечно, выглядит чрезмерно упрощенной.

Входящая в уравнение (9.1) собственная частота атомного электрона может быть рассчитана только на основе квантовой теории атома. В рамках классической теории её следует рассматривать как формально введенную константу, которая определяет линию поглощения в спектре исследуемого вещества. Постоянная затухания, характеризующая «силу сопротивления», содержит вклад, обуславливаемый радиационным затуханием.

Для монохроматической волны решение (9.1) описывающее установившееся вынужденное колебания электрона, будем искать в виде:

. (9.2)

Амплитуду найдем, подставляя (9.2) в (9.1)

. (9.3)

В общем случае в правой части (9.3) вместо должно стоять значение средней макроскопической напряженности , входящей в уравнение Максвелла, однако в разряженных средах можно приять, что .

Индуцированный дипольный момент , поэтому:

. (9.4)

Поскольку поляризованность , где - концентрация атомов вещества (у каждого атома по одному оптическому электрону), - диэлектрическая восприимчивость, , то учитывая, что диэлектрическая проницаемость , из (9.4) получим:

. (9.5)

Из (9.5) следует, что является комплексной величиной:

. (9.6)

Введём аналогичные выражения для показателей преломлении:

, (9.6’)

где - комплексный показатель преломления, – показатель затухания. Используя , из (9.6), (9.6’) получим:

(9.7)

Выделяя реальную и мнимую части в (9.5), найдем:

, (9.8)

(9.9)

При малых значение , полагая что , преобразуем (9.8) и (9.9) к виду:

, (9.8’)

. (9.9’)

Частотные зависимости и приведены на рис. 9.1.

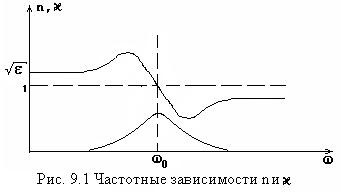
На частотах далеких от , где выполняется условие , вторым слагаемым в знаменателе (9.8’) можно пренебречь:

. (9.10)

Рассматривая как малый параметр получим:

, (9.11)

где - так называемая плазменная частота.

Переходя от частоты к длине волны (в вакууме) , получим простую формулу для сравнения с экспериментальными данными:

, (9.12)

где , .

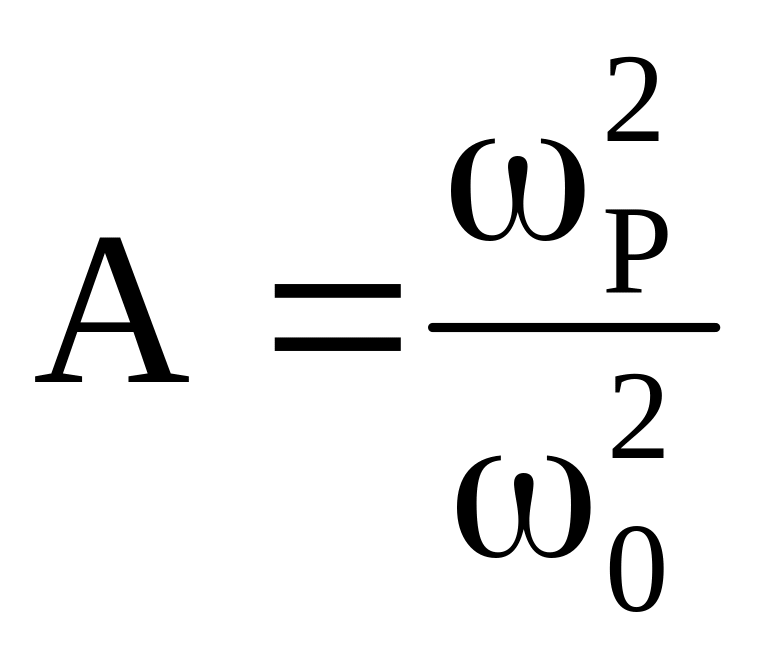Выражение с эмпирическими коэффициентами подобное (9.12), до появления электронной теории дисперсии было получено Френелем и Коши.

Величина дисперсии определяется производной . При дисперсию называют нормальной, при - аномальной. Из рис. 9.1 видно, что область аномальной дисперсии находится в близи . Таким образом, любое вещество, у которого , обладает областями нормальной и аномальной дисперсии.