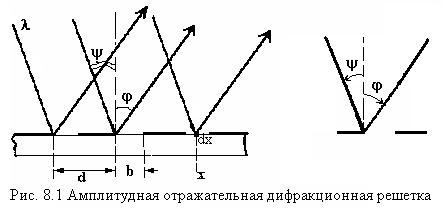
1. Дифракция Фраунгофера на n щелях

Пусть на систему из N строго периодических щелей (период ) падает плоская монохроматическая волна под углом к плоскости решетки (см. рис. 8.1).

Для определения зависимости интенсивности от угла дифракции проведем процедуру, аналогичную соотношениям 7.1-7.4 с той лишь разницей, что вместо двух щелей рассмотрим N щелей. Итак, от элемента n-ой щели, который расположен на расстоянии от ее начала, возбуждается волна, распространяющаяся под углом :

, (8.1)

где А – константа, - волновое число.

Вся n-я щель пошлет в направлении угла волну:

(8.2)

Интерференция волн от всех N щелей приводит к следующему:

. (8.3)

Вычисляя (8.3) получим:

, (8.4)

(8.5)

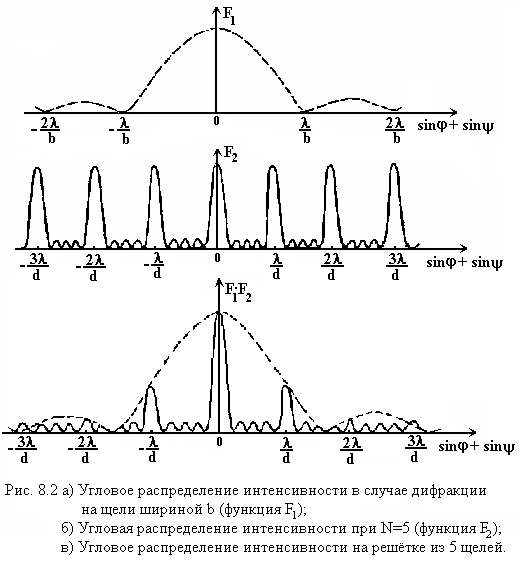
где , , - множитель, определяющий амплитуды максимумов (моделирующая функция), соответствующей (6.8) для дифракции Фраунгофера на одной щели, - множитель, определяющий распределение максимумов и минимумов. Угловые зависимости и при N=5 представлены на рис. 8.2.

Условие:

, (8.6)

где , называется условием главных максимумов. При пользовании (8.6) следует иметь в виду, что и отсчитываются от нормали к плоскости решетки и являются положительными, если отсчитываются в направлении против часовой стрелки.

Нули функции определяются соотношением:

, (8.7)

где , то есть между соседними главными максимумами находится минимумов (нулей). Между дифракционными нулями находится второстепенных максимумов (см. рис. 8.2).

1.2 Основные характеристики амплитудных решеток. Угловая дисперсия

Дисперсия D характеризует угловое расстояние между двумя близкими спектральными линиями (например, между желтыми линиями излучения паров ртути). Используя условие главного дифракционного максимума (8.7) для D, получим:

(8.8)

На опыте угловую дисперсию решетки определяют путем деления измеренного углового расстояния между двумя близкими линиями излучения на известную разность длин волн этих линий (см. соотношение 8.8).

Разрешающая способность решетки

Разрешающей силой дифракционной решетки называется отношение:

, (8.9)

где - расстояние межу спектральными линиями, удовлетворяющее критерию Рэлея. В соответствии с критерием Рэлея разрешение спектральных линий происходит в том случае, когда главный максимум -го порядка для дин волн совпадает с первым минимумом (нулём), находящимся справа от -го порядка главного максимума волны . В соответствии с (8.6) и (8.7) мы за­пишем

, (8.10)

.

Решая (8.10 относительно ) и подставляя найденное выражение в (8.9, получим:

. (8.13)