2. Описание экспериментальной установки

Схема для наблюдения дифракции Френеля

Схема установки для наблюдения дифракции Френеля на круглом отверстии и щели приведена на рис. 6.7.

Свет от гелий-неонового лазера (плоская волна с ) падет на экран Э с круглым отверстием радиуса или с регулируемой щелью. Дифракционная картина формируется в плоскости П. Поскольку размеры дифракционной картины малы, что затрудняет ее исследование, то с помощью короткофокусной линзы К ( = 20 мм) она проецируется на плоскость П'. Для рассматриваемой установки соотношение (6.8) преобразуется к виду:

. (6.27)

Расстояние определяется из формулы тонкой линзы и рис. 6.7.

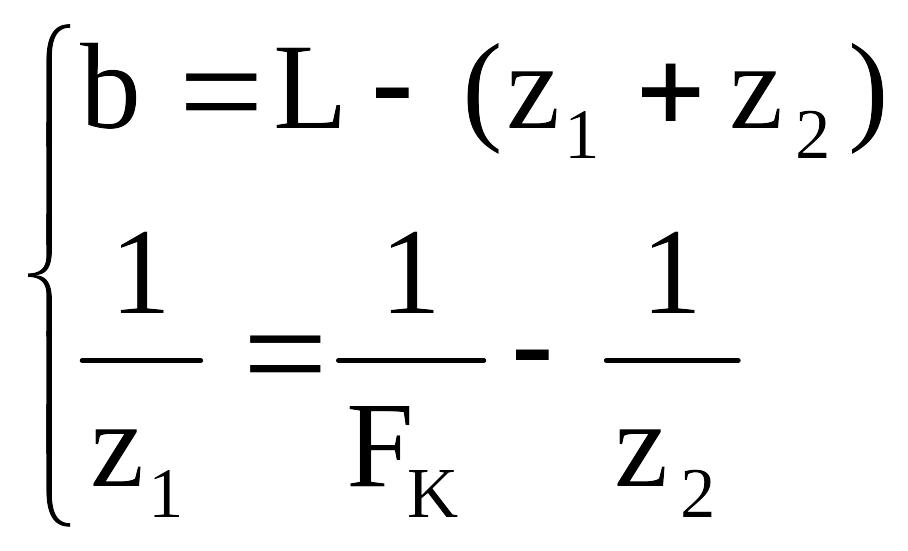(6.28)

При , , поэтому вместо (6.27) можно использовать приближенное соотношение:

(6.29)

Если при неизменном радиусе отверстия перемещать экран Э, то число зон Френеля для точки P будет изменяться в соответственном с (6.26) по закону:

, (6.30)

где – значение , соответствующее -ой зоне Френеля.

Интенсивность в точке P при различных значениях будет изменяться в соответствии с графиком, представленным на рис. 6.3. Отметим, что исследовать зависимость (6.29) следует с определения (для двух зон Френеля в точке P будет минимум), которое равно половине (см. рис. 6.3). Аналогично следует действовать и при исследовании дифракции Френеля на щели.

Схема для наблюдения дифракции Фраунгофера

Для наблюдения дифракции Фраунгофера можно воспользо­ваться схемой, приведенной на рис. 6.6 удалив из нее линзу К. При этом расстояние от точки наблюдения до отверстия, радиус отверстия (или полуширина щели) должны удовлетворять условию (6.20), которое в нашем случае превращается в:

. (6.31)

Полагая, что , , получим , следовательно, при можно наблюдать дифракцию Фраунгофера.

При исследовании дифракции на отверстии прямоугольной формы ( – размеры отверстия вдоль и ), необходимо измерить распределение интенсивности вдоль и . Углы дифракции определяются следующими соотношениями:

. (6.32)

3. Порядок выполнения работы Упражнение 1 Исследование дифракции Френеля на круглом отверстии

Установите на пути лазерного луча приспособление, позво­ляющее перемещать экран с круглым отверстием относительно лин­зы К (см. рис. 6.6). Включите лазер и получите дифракционную картину на экране П', который расположите на расстоянии от линзы К.

Перемещая экран Э относительно линзы К, определите значение ,при котором открыто две зоны Френеля относи­тельно точки P. При этом на светлом фоне в центре изображения наблюдается темное пятно. Приближая экран Э к линзе К, определите по чередующимся максимумам и минимумам в соответствии с рис. 6.3. так, при =3 на светлом фоне в центре изображения наблюдается светлое пятно, окруженное темным контуром. Используя полученные постройте график зависимости . Из (6.27) следует, что это прямая тангенс угла наклона которой равен , откуда, зная значение ( ), определите радиус круглого отверстия.