2.2 Дифракция Френеля на щели

При наблюдении дифракции Френеля на краю экрана или щели источник должен быть линейным или излучать плоскую волну. Ограничимся рассмотрением плоской волновой поверхности, падающей на экран волны:

. (6.14)

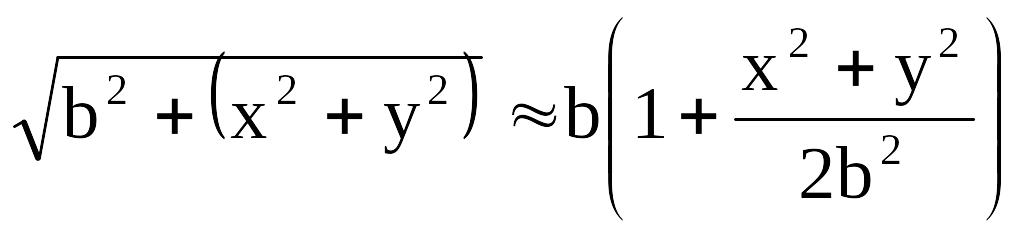При малых углах можно принять , а , при . В результате:

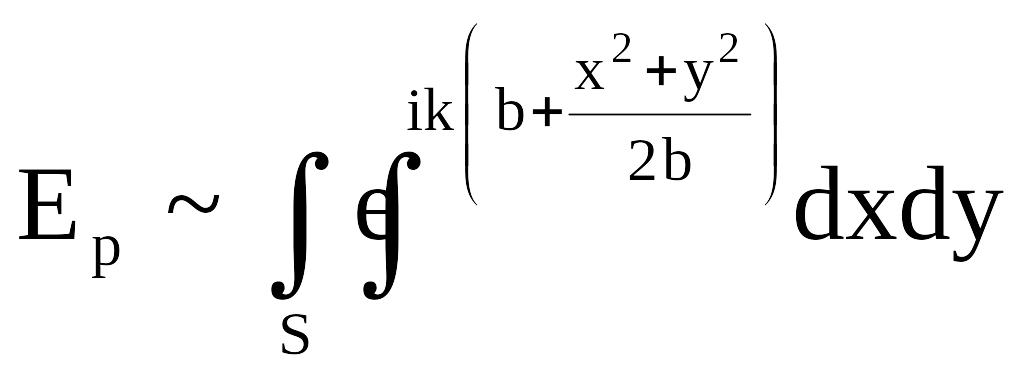. (6.14’)

Если граничить волновую поверхность щелью, расположенной вдоль оси У, то (6.14’) преобразуется в:

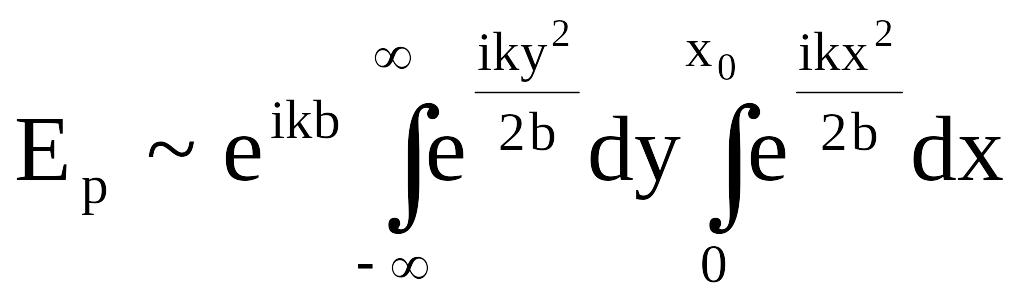. (6.15)

Интеграл по у равен , поэтому

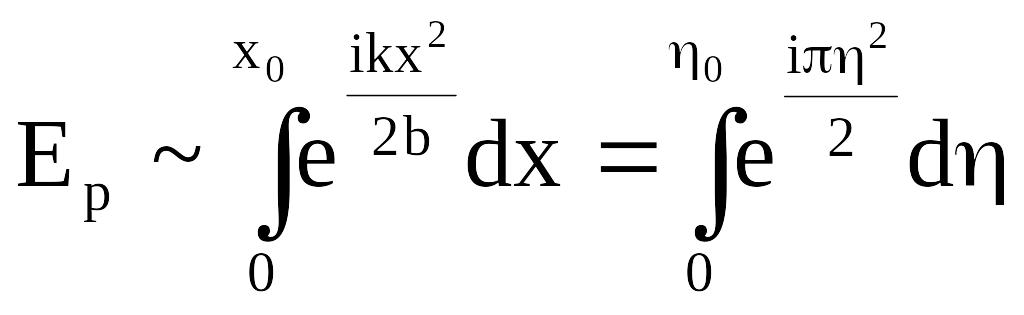. (6.16)

Выражение (6.16) представляет собой интеграл Френеля, где , то есть:

, (6.17)

где – координата края щели, открывающей пространство .

Вычисления по формуле (6.16) удобно проиллюстрировать с помощью векторной диаграммы, аналогично тому, как это было сделано для круглого отверстия, разбив плоскую волновую поверхность на зоны, в пределах каждой их которых фаза волны, создаваемой в точке Р изменяется на . эти зоны называются зонами Шустера. Пусть точка Р находится над неподвижном краем щели, координата перемещаемого края – . Несложно показать, что при координата перемещаемого края щели, открывающей зон Шустера равна:

, (6.18)

то есть площадь -ой зоны:

(6.19)

быстро убывает при малых значениях и почти не изменяется при больших . В результате, векторная диаграмм представляет собой спираль (см. рис. 6.4), называется спиралью Корню. Цифры на диаграмме означают величину из (6.17). Аналитически спираль является результатом вычисления значений интеграла (6.16), представленных на комплексной плоскости.

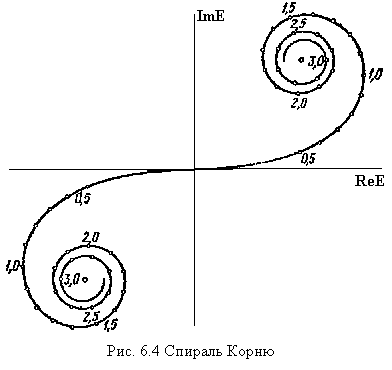
Из рис. 6.4 видно, что в отличие от дифракции на круглом отверстии максимумы и минимумы интенсивности в точке Р лишь приближенно соответствуют целому числу открытых зон Шустера.

Точный расчет распределения интенсивности вне точки в обоих случаях представляет собой сложную задачу. По этой причине выше излагается приближенный метод вычисления интенсивности только для точки с помощью построения зон Френеля или Шестера. Отметим, что дифракционная картина для круглого отверстия представляет собой чередующиеся светлые и темные кольца, для щели – светлые и темные полосы (параллельные расположению щели), при этом в центре этой картины в зависимости от четности количества открытых зон в соответствии с рис. 6.2 и 6.4 будет минимум ( – четное) или максимум ( – нечетное).

2.3 Дифракция Фраунгофера

Используя выражение (6.8) и рис. 6.2 и 6.3, можно убедиться в том, что чередование максимумов и минимумов интенсивности в точке Р будет происхо­дить при условии, когда радиус отверстия отвечает условию , где .

Это чередование исчезает при выполнении условия:

, (6.20)

которое является критерием перехода от дифракции Френеля к дифракции Фраунгофера. При этом закономерности, отмеченные выше, не выполняются.

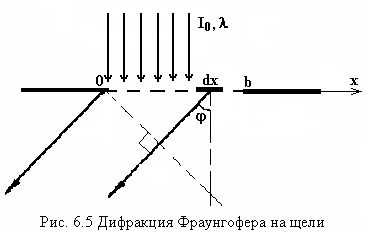
Предельным случаем дифракции Фраунгофера является дифракция в параллельных лучах. Расчет зависимости интенсивности от угла дифракции можно произвести, используя рис. 6.6. Элемент щели , который находится на расстоянии от точки , возбуждает в направлении угла колебание . В соответствии с рис. 6.5 и принципом Гюйгенса-Френеля для можно записать следующее выражение:

, (6.21)

где – амплитуда колебаний электрического поля плоской волны.

Проинтегрируем выражение (6.21) по всей щели:

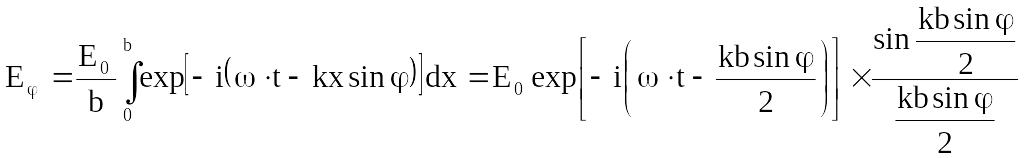(6.22)

Для интенсивности , учитывая (6.22),получим:

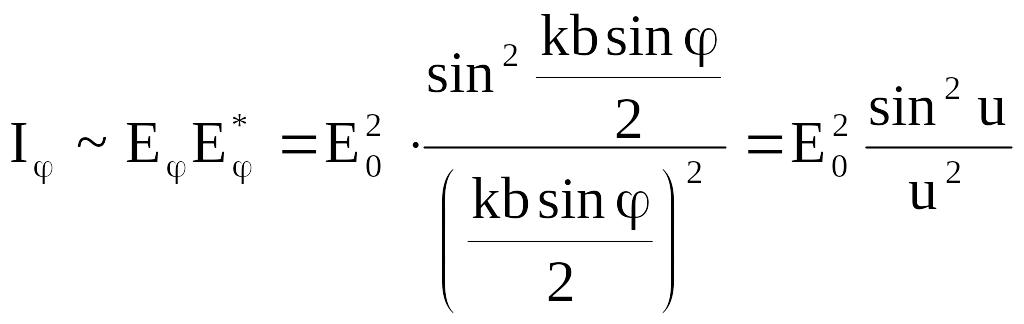, (6.23)

где .

Анализируя выражение (6.23), легко получить условие мини­мума интенсивности:

. (6.24)

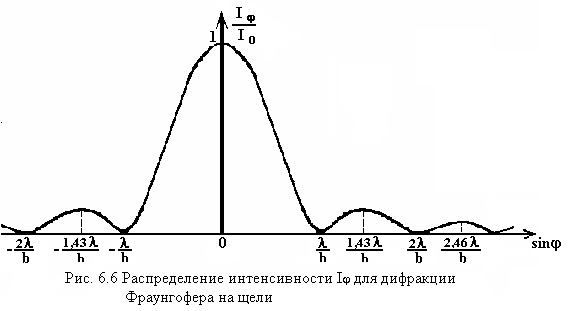
Для максимума функции (6.23) получим трансцендентное урав­нение типа , корни решения которого равны:

. (6.25)

Для прямоугольного отверстия самостоятельно провести вывод распределения интенсивности для угла дифракции:

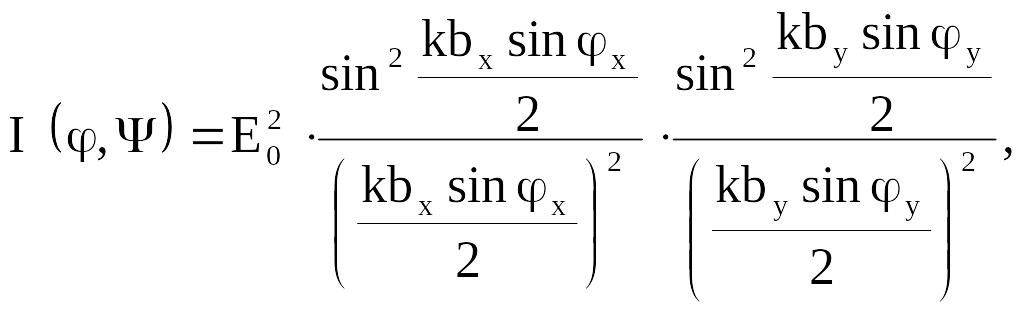(6.26)

где и – размеры прямоугольного отверстия.