Упражнение 2

Определение длины волны пропускания неизвестного светофильтра

1. На столике осветителя поместить светофильтр с неизвестной длиной волны, которую он пропускает. Проделайте пункты 3 и 4 упражнения 1, и определите из тангенса угла наклона аппроксимирующей прямой (5.6), используя - среднее значение радиуса кривизны линзы, полученное в упражнении 1.

2. Определите и погрешности измерения с учетом погрешностей .

Упражнение 3 Определение полосы пропускания светофильтров

Зная значения наблюдаемых максимальных порядков интерференционных колец для трех светофильтров, оценить полосы про­пускания каждого светофильтра. Соответствующую формулу расчета этой полосы получить самостоятельно, опираясь на теорию интер­ференции в тонких пленках.

Контрольные вопросы и задания

1. Сформулируйте условия наблюдения полос равной толщины, равного наклона.

2. Объясните появление дополнительной разности хода в выражениях (5.1), (5.2).

3. Чем обусловлено конечное число наблюдаемых в тонких пленках интерференционных полос?

4. Какие погрешности эксперимента устраняет графический метод обработки результатов?

5. Из графика (5.6) оцените величину прослойки между поверхностями линзы и плоской пластинкой (может оказаться, что линза «вдавлена» в поверхность пластинки).

6. Почему в работе рекомендуется измерять радиусы тёмных, а не светлых колец?

7. Как измениться интерференционная картина, если пространство между линзой и плоскостью заполнить жидкостью?

8. Сравните интерференционные картины, наблюдаемые в проходящем и отраженном свете.

ЛАБОРАТОРНАЯ РАБОТА № 6

ИЗУЧЕНИЕ ДИФРАКЦИИ СВЕТА

1. Теоретические основы дифракции

В узком (наиболее употребимом) смысле дифракция – это явление огибания световыми лучами непрозрачных тел и, следовательно, проникновения света в область геометрической тени. В широком смысле – это проявление волновых свойств света в условиях, близких к условиям применимости геометрической оптики.

1. Дифракция Френеля на круглом отверстии

Согласно принципу Гюйгенса-Френеля, каждый бесконечно малый элемент волнового фронта следует рассматривать как источник вторичных волн. Колебания в произвольной точке пространства является результатом интерференции сферических волн, излучаемые этими вторичными источниками.

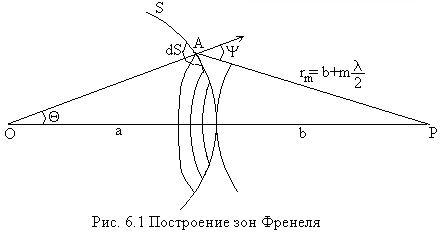
Рассмотрим волну, излучаемую точечным монохроматическим источником О. такая волна является сферической (см. рис. 6.1). На расстоянии от источника ее напряженность:

, (6.1)

где – циклическая частота,

– волновое число.

Элемент сферической поверхности площадью создает колебания в точке :

, (6.2)

где – расстояние от точки волнового фронта до точки Р,

– угол между нормалью к площади и напряжением луча,

– коэффициент дифракции, который принимает максимальное значение при и равен нулю при (последнее выражает отсутствие обратной волны).

Интегрируя по всей поверхности и полагая, что на расстоянии 1 м от источника О, напряженность равна , получим:

, (6.3)

Взять интеграл (6.3) невозможно, так как неизвестна зависимость . Однако, если с ростом убывает медленно, можно разбить волновую поверхность на зоны (так называемые «зоны Френеля»), в пределах каждой из которых фазы излучаемых волн в точке Р изменяются на , а , оставаясь постоянным в пределах одной зоны, убывает сростом номера зоны. Зоны Френеля – это кольцевые зоны на волновой поверхности , ограниченные окружностями, полученные путём сечения фронта сферами с центром в точке Р, радиусами . В этом случае (6.3) преобразуется к виду:

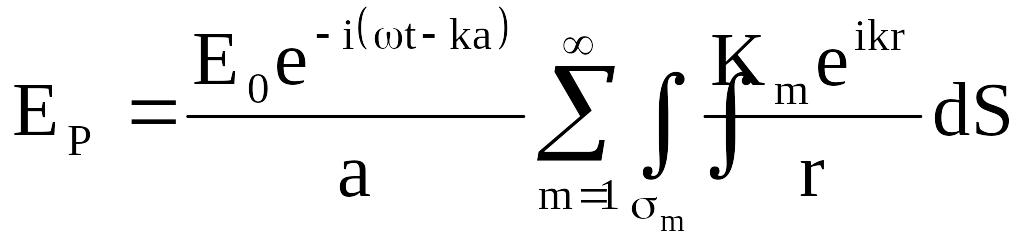, (6.4)

где – площадь m-ой зоны Френеля.

В пределах m-ой зоны изменяется от до . Найдём как функцию . Из рис 6.1 можно получить:

. (6.5)

Дифференцируя (6.5) и учитывая, что , получим:

. (6.6)

Поскольку в пределах одной зоны изменяется на , подставляя в (6.6), найдем площадь одной зоны Френеля:

. (6.7)

Поскольку , то окончательно:

, (6.7’)

то есть площади зон одинаковы.

Радиус m-ой зоны Френеля определяется выражением:

. (6.8)

Подставляя (6.6) в (6.4) сводит решение (6.4) к вычислению суммы элементарных интегралов:

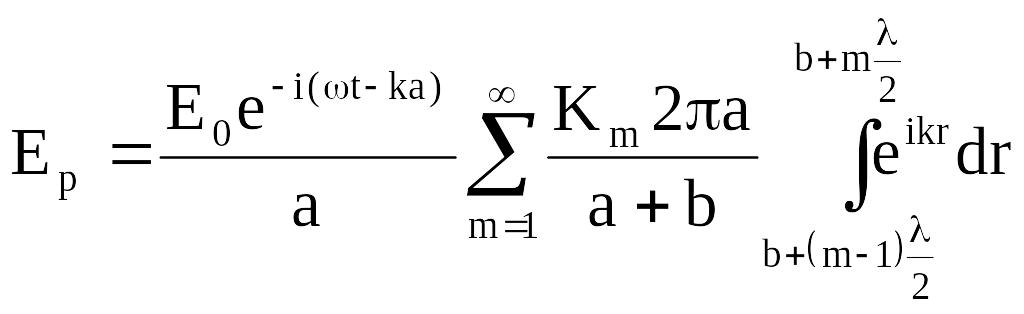. (6.9)

Из (6.9) следует, что

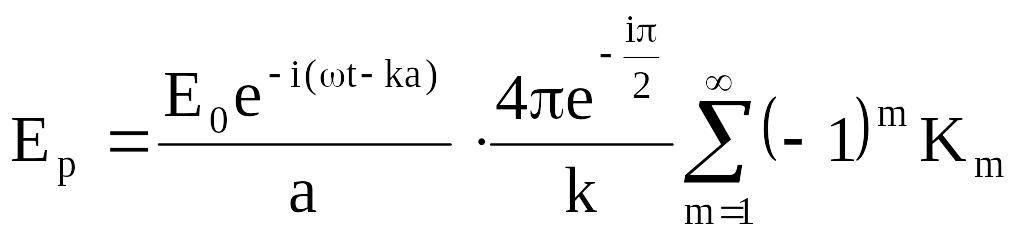. (6.10)

Множитель в (6.10) означает, что фазы колебаний, создаваемых в точке Р соседними зонами отличаются на , в результате:

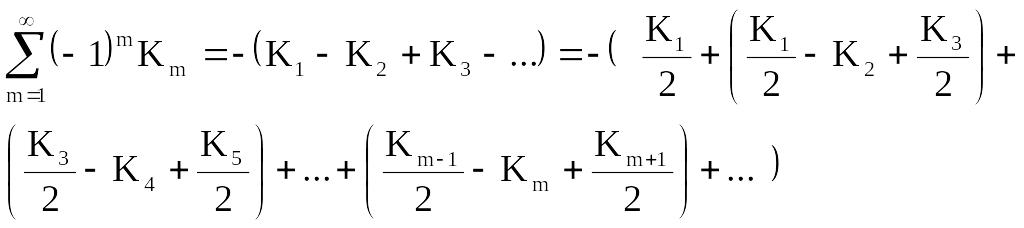, (6.11)

где , то есть с ростом убывает медленно.

Если волновая поверхность ограничена крупной диафрагмой (круглое отверстие), открывающей зон Френеля, то

, (6.12)

где «+»соответствует нечётному, а «–» - чётному , а поскольку .

, (6.13)

где – возмущение в P от первой зоны Френеля,

– от -ой зоной Френеля.

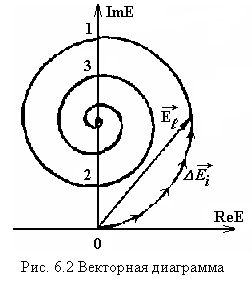
Результат (6.9), (6.13) удобно интерпретировать с помощью вектор­ной диаграммы (на комплексной плоскости вектор характеризуется амплитудой и фазой) (см. рис. 6.2).

Разобъём каждую зону Френеля на подзон, в пределах каждой из которых фаза волн в точке Р измениться на . Понятно, что площадь этих подзон одинаковы, так как одинаковы площади зон Френеля, и следовательно результирующее колебание в точке Р , создаваемое в пределах одной зоны Френеля, представляет собой полуокружность на комплексной плоскости. А поскольку убывает с ростом , то векторная диаграмм из окружности превращается в закручивающуюся спираль.

Точки 1, 2, 3 на рис. 6.2 относятся к периферийным точкам одной, двух или трех зон Френеля для . Электрическое поле в точке P для одной, двух и большего числа зон Френеля равно величине вектора, соединяющего точку с соответствующими точками 1, 2, 3 и т.д. С увеличением номера зоны Френеля (это приводит к увеличению угла дифракции ) монотонно уменьшается, что приводит к уменьшению величины – напряженности поля, создаваемого в точке Р зоной Френеля. С помощью такой диаграммы легко объяснить характер поведения интенсивности излучения в точке P (интенсивность ) для малых значения при увеличении радиуса отверстия или уменьшения величины . 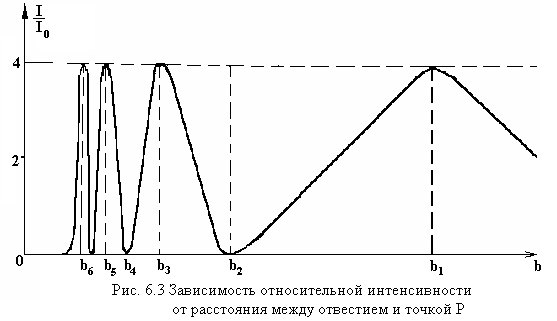На рис. 6.3 представлена зависимость относительной интенсивности света ( , где ) от расстояния , а, следовательно, от количества открытых зон Френеля. Значение соответствует одной открытой зоне Френеля при заданных , , где - радиус отверстия в непрозрачном экране.