111

Федеральное агентство по образованию

(Рособразование)

Ярославский государственный университет им. П.Г.Демидова

В.А. Папорков, Е.В. Рыбникова

Оптика

Лабораторный практикум

Учебное пособие

Ярославль 2006

ББК В38 я 73

П

Рецензенты: кафедра физики Ярославского государственного технического университета, доцент кафедры теоретической и экспериментальной физики Ярославского государственного педагогического университета канд. физ.-мат. наук Г. В. Жусь.

Составители: Папорков В.А., Рыбникова Е.В.

Оптика. Лабораторный практикум: Учеб. пособие / Папорков В.А., Рыбникова Е.В.; Яросл. гос. ун-т. Ярославль, 2006. … с

ISBN 5-8397-0289-7

Данное пособие представляет собой руководство к выполнению лабораторных работ по дисциплине «Оптика» (ЕН) и предназначено для студентов второго курса очной формы обучения специальностей 010400 «Физика».

Пособие содержит краткую теорию исследуемых физических явлений, методику измерений и обработки результатов, перечень контрольных вопросов и заданий по каждой лабораторной работе, список литературы.

© Ярославский государственный университет, 2006

© Папорков В.А., Рыбникова Е.В.

ЛАБОРАТОРНАЯ РАБОТА № 1.

ОПРЕДЕЛЕНИЕ ФОКУСНЫХ РАССТОЯНИЙ ПОЛОЖИТЕЛЬНЫХ И ОТРИЦАТЕЛЬНЫХ

СФЕРИЧЕСКИХ ЛИНЗ.

1. Теория сферической тонкой линзы

Сферическая линза представляет собой пространство, ограниченное двумя сферическими поверхностями. Прямая, соединяющая центры кривизны этих поверхностей, является главной оптической осью такой линзы. Линза называется тонкой, если ее толщина вдоль главной оптической оси существенно меньше радиусов кривизны ее поверхностей. В зависимости от кривизны поверхностей и соотношения коэффициентов преломления материала линзы и среды, в которой находится линза, она может быть собирающей (положительной) или рассеивающей (отрицательной). Целью этой работы является изучение методов определения фо­кусных расстояний положительных и отрицательных сферических тонких линз.

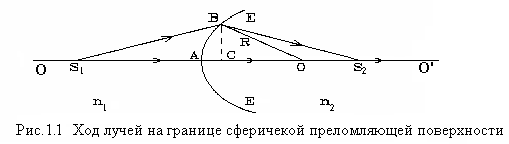
Для реализации этой цели рассмотрим свойства сферической преломляющей поверхности ЕЕ' (см. рис. 1.1) с радиусом кривиз­ны R, которая разделяет две среды с показателями преломления и . Слева от ЕЕ' находится точечный источник . Точка является изображением источника , если любой паракси­альный луч (условие параксиальности ) после пре­ломления на ЕЕ' пройдет через . Это возможно при выполнении равенства оптического пути:

или иначе

. (1.1)

Рассмотрим треугольники .

(1.2)

Начало отчета, как правило, помещают в точку пересечения сферической поверхности с оптической осью в этом случае: .

Вводя обозначение: и подставляя (1.2) в (1.1), получим:

. (1.3)

Учитывая, что , преобразуем (1.3) к виду:

, (1.3’)

а поскольку для параксиальных лучей , то окончательно:

. (1.4)

Выражение (1.4) определяет оптическую силу Ф сферической поверхности.

Если источник удален на бесконечность, т.е. , то

. (1.5)

В случае, когда источник находится справа от поверхности ЕЕ' на расстоянии ,

(1.6)

Значения и , определяемые выражениями (1.5) и 1.6), называются фокусными расстояниями сферической поверхности ЕЕ'.

Рассмотрим двояковыпуклую тонкую линзу (см.рис. 1.2), определяемую двумя сферическими поверхностями с радиусами кривизны и , и показателем преломления . Показатели преломления сред слева и справа от линзы обозначим через и .

Построим изображение точечного источника , находящегося на главной оптической оси линзы. Для этого построим промежуточное изображение этого источника , формируемое сферической поверхностью 1, которая разделяет среды с показателями преломления и . Согласно (1.4) запишем:

, (1.7)

где - оптическая сила первой поверхности.

Изображением является точка , для которой, согласно (1.4),

, (1.8)

где - оптическая сила второй поверхности.

Полагая и складывая (1.7) и (1.8), получим:

, (1.9)

где - оптическая сила тонкой сферической линзы.

Фокусные расстояния и определяются аналогично (1.5), (1.6):

. (1.10)

Выражение

(1.11)

называется формулой тонкой линзы. В рассматриваемом на рис. 1.2 случае .

2. Погрешности линз

Сферическая аберрация При использовании всей поверхности сферической линзы для построения изображения точечного источника оказывается, что края линзы отклоняют лучи сильнее, чем требуется для прохождения их через изображение, даваемое средней частью линзы. В результате этого изображе­ние точечного источника на экране получается в виде расплыв­чатого пятна. Для устранения этой аберрации следует либо уменьшать апертуру пучка света, либо усложнять оптическую систему, включая в нее отрицательную линзу.

Кома Для линз, исправленных на сферическую аберрацию, для источника, лежащего на главной оптической оси, может сохраняться сферическая аберрация для источника, расположенного в стороне от главной оптической оси. Такая аберрация называется комой. При наличии комы изображение точечного источника представляет собой вытянутое пятно. Соответствующей комбинацией положительных и отрицательных линз можно избавиться от такой аберрации.

Астигматизм Радиусы кривизны оптических поверхностей в двух взаимно перпендикулярных плоскостях, проходящих через оптическую ось линзы, могут оказаться различными. В этом случае изображение точечного источника имеет вид двух взаимно перпендикулярныx прямолинейных отрезков. Этот вид аберрации устраняется путем подбора радиусов кривизны и оптических сил преломляющих по­верхностей.

Дисторсия Дисторсия - это аберрация, которая обуславливает неодинаковость поперечного увеличения в пределах поля зрения. Если увеличение возрастает с удалением от оптической оси, имеет место подушкообразная дисторсия. При уменьшении увеличения - бочкообразная.

Хроматическая аберрация Рассмотренные выше аберрации свойственны всем оптическим системам для любой области спектра (в том числе и для монохроматического излучения). Хроматическая аберрация обусловлена явлением дисперсии вещества линзы (зависимостью коэффициента преломления от длины волны). Дисперсия материала линзы обуславливает зависимость фокусного расстояния линзы (1.11) от длины волны. Это обстоятельство приводит к тому, что изображение немонохроматического источника для разных длин волн (цветов) находится на разных расстояниях, что определяет окрашивание контура изображения. Комбинируя линзы, изготовленные из различных материалов, удаётся создать ахроматичную (то есть исправленную на хроматическую аберрацию) оптическую систему.

Отметим, что для одновременного устранения всех видов аберраций линзы требуется составить весьма сложную оптическую систему (современные объективы представляют системы, состоящие из большого количества линз). По этой причине в каждом конкретном случае стараются устранить самые существенные аберрации.

3. Порядок выполнения работы

В работе все измерения проводятся на оптической скамье, вдоль которой перемещаются рейтеры с линзами, экраном, осветителем. Перед выполнением работы следует убедиться в параллельности оптических осей линз ребру оптической системы.

Отсчет расстояний между деталями оптической скамьи производится по указателям на основании рейтеров. В окне осветителя установлена щелевая диафрагма, играющая роль предмета. Вплотную к осветителю помещается светофильтр.