Визначте загальний індекс витрат часу на одиницю продукції

Відповіді: а) 0,90; б) 1,11; в) 0,906; г) 0,875.

22. Відомі наступні дані по двох заводах (див. табл.).

Визначте індекс середньої собівартості постійного складу.

Відповіді: а) 0,962; б) 0,987; в) 0,988; г) 0,975.

Номер заводу	Виробництво продукції, тис. шт.		Собівартість 1 шт. грн.
	1 квартал	2 квартал	1 квартал	2 квартал
№ 1	15,0	25,0	5,8	5,5
№ 2	35,0	25,0	6,2	6,2
Разом	50,0	50,0	Х	Х

23. Відомі наступні дані про продаж бензину:

Марка бензину	Обсяг реалізації, літрів		Ціна 1 літру, грн.
	базисний період	звітний період	базисний період	звітний період
А – 98	20000	10000	5,5	6,0
А – 80	5000	5000	3,0	3,0

Визначте індекс середньої ціни змінного складу літру бензину. Відповіді: а) 0,950; б) 0,875; в) 0,910; г) 1,000

24. Відомі наступні дані по одному з магазинів:

Вид тканей	Реалізовано, тис. м.		Ціна за 1 м., грн.
	1 квартал	2 квартал	1 квартал	2 квартал
Ситець	2,0	1,8	13,0	15,0
Шовк	4,0	5,0	3,5	3,0

Визначте загальний індекс товарообігу.

Відповіді: а) 1,33; б) 0,952; в) 1,091; г) 1,050.

25. Відомі наступні дані про реалізацію магазином побутової техніки:

Найменування товарів	Реалізовано товарів у фактичних цінах, тис. грн.		Зміна цін у звітному періоді порівняно з базисним, %
	базисний квартал	звітний квартал
Кондиціонери	600	676	-15,5
LCD телевізори	500	528	-12,0

Визначте загальну зміну цін по двом товарам у звітному періоді порівняно з базисним, %.

Відповіді: а) 86,25; б) 86,0; в) 109,4; г) 94,2.

6 Вибірковий метод

6.1 Основні поняття вибіркового методу

Вибіркове спостереження – вид не суцільного спостереження, при якому обстежують не всі елементи сукупності, що вивчається, а лише певним чином дібрана їх частина. Сукупність з якої вибирають елементи для обстеження, називається генеральною, а сукупність яку обстежують – вибірковою. Статистичні характеристики вибіркової сукупності розглядаються як оцінки відповідних характеристик генеральної сукупності.

Практика вибіркових спостережень досить різноманітна. Це обстеження домогосподарств, маркетингові дослідження, аудиторські перевірки, вивчення громадської думки тощо. При обстежені невеликої частки генеральної сукупності зменшуються помилки реєстрації, можна розширити й деталізувати програму обстежень. З іншого боку вибіркове спостереження забезпечує економію матеріальних, трудових, фінансових ресурсів та часу.

В окремих випадках вивчення певного кола соціально-економічних явищ вибіркове спостереження єдино можливе. Це стосується передусім перевірки якості продукції (зольність вугілля, жирність молока, чистота та вологість зерна, міцність пряжі тощо). Часом вибіркове спостереження поєднується із суцільним. Наприклад, при перепису населення кожна четверта одиниця спостереження дає докладнішу інформацію.

Об’єктивною гарантією того, що вибірка репрезентує (представляє) всю сукупність, є додержання наукових принципів організації та проведення спостереження, насамперед неупередженого, об’єктивного підходу до відбору елементів для обстеження. Принцип випадкового вибору забезпечує всім елементам генеральної сукупності рівні можливості потрапити у вибірку.

Оскільки вибіркова сукупність не точно відтворює склад генеральної сукупності, то й вибіркові оцінки не збігаються з відповідними характеристиками генеральної сукупності: для середньої – це різниця між генеральною ( ) та вибірковою ( ), для частки – різниця між генеральною ( ) і вибірковою (p) частками, для дисперсії – відношення генеральної ( ) та вибіркової ( ) дисперсій тощо.

Подивимося на показники генеральної та вибіркової сукупності на конкретному прикладі.

Приклад 6.1 Припустимо, що генеральну сукупність складають робітники цеху, які розподілені за розміром заробітної плати (див. табл. 6.1).

Таблиця 6.1 – Розподіл робітників цеху за розміром заробітної плати

Місячна заробітна плата одного робітника, грн.	Чисельність робітників
240	10
260	10
280	50
300	30
Разом	100

За наведеними даними розрахуємо середню заробітну плату, частку робітників із заробітною платою 280 грн. та більше, генеральну дисперсію та середнє квадратичне відхилення.

Середня заробітна плата:

Генеральна дисперсія:

Середнє квадратичне відхилення:

Генеральна частка:

Далі припустимо, що з цієї генеральної сукупності у випадковому порядку відібрано 20 робітників, розподіл яких за розміром заробітної плати наведено у таблиці 6.2.

Обчислимо вибіркову середню, вибіркову дисперсію, вибіркову частку та середнє квадратичне відхилення для отриманої вибірки.

Середня заробітна плата для вибіркових даних:

Таблиця 6.2 – Розподіл 20 робітників цеху за розміром заробітної плати

Місячна заробітна плата одного робітника, грн.	Чисельність робітників
240	3
260	5
280	7
300	5
Разом	20

Вибіркова дисперсія:

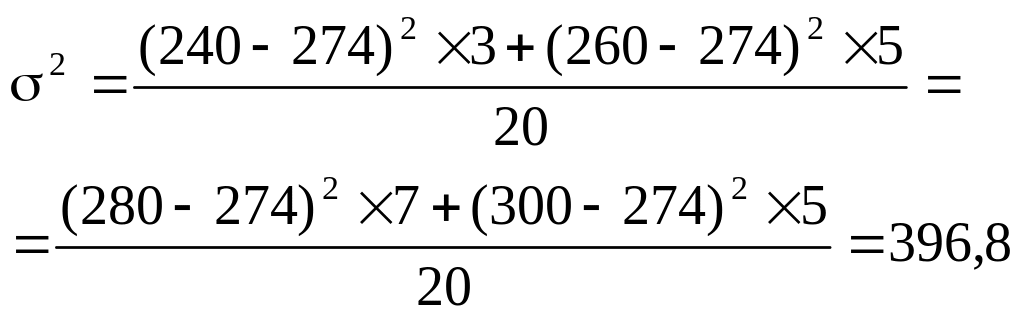
Середнє квадратичне відхилення для вибірки:

Вибіркова частка:

Зведемо обчислені показники у порівняльну таблицю 6.3.

Як видно з наведеного прикладу однакові показники генеральної та вибіркової сукупності не співпадають.

Розбіжності між ними називають похибками репрезентативності.

Таблиця 6.3 – Порівняння показників генеральної і вибіркової сукупності

Показники	Генеральна сукупність	Вибіркова сукупність	Відхилення
Середня заробітна плата, грн.	280	274	+6
Середнє квадратичне відхилення	17,9	19,9	-2
Частка робітників із заробітною платою 280 грн. та більше	0,8	0,6	+0,2 (+20%)