4.4 Аналітичне вирівнювання

Ковзна середня характеризує загальну тенденцію розвитку явища, не дає аналітичного вираження тренду. З цією метою вдаються до аналітичного вирівнювання ряду динаміки. Це здійснюється у декілька етапів:

1. На підставі апріорного аналізу сутності і законів розвитку

встановлюється можливий характер динаміки явища, що досліджується.

2. Виходячи з характеру динаміки, обирається форма аналітичного рівняння, яка найкращим чином відображає закономірність динаміки явища: пряма, парабола, гіпербола і т. ін.

3. Обчислюються параметри обраного рівняння зв’язку.

Таким чином, технічно вирівнювання полягає у заміні фактичних рівнів такими рівнями, що плавно змінюються (теоретичними), котрі у середньому менше всього відхилялися би від фактичних і мали би визначений аналітичний вираз, відповідно загальному напрямку і характеру тренда.

Розглянемо процес вирівнювання ряду динаміки по прямій.

Приклад 4.5. Відомі дані про собівартість промислового продукту “А” за роками, грн/кг. (див. табл. 4.7)

Позначимо собівартість через “y”, час через “t” тоді рівняння, що пов’язує зміну собівартості у часі буде мати вигляд:

(4.1)

де t – час, порядкові номера періодів або моментів часу, до яких відносяться рівні ряду.

Таблиця 4.7 – Дані про собівартість промислового продукту “А” по роками, грн/кг

Роки	Собівартість ( )	Роки (умовно),
1	2	3	4	5	6
2004	7,7	-2	4	-15,4	8,68
2005	9,4	-1	1	-9,4	9,23
2006	11,2	0	0	0	9,78
2007	10,9	1	1	10,9	10,33
2008	9,7	2	4	19,4	10,88
Разом	48,9	0	10	5,5	

Спеціальні методи дозволяють отримати параметри аналітичної формули, які найкращим чином охоплюють точки рівней ряду. Основним таким методом є метод найменших квадратів. В його основі лежить умова: сума квадратів відхилень конкретних (заданих) значень від розрахованих по рівнянню (4.1) повина бути мінімальною:

(4.2)

де n – число рівнів.

Цієї умові задовольняє система нормальних рівнянь:

, (4.3)

Звідси легко знайти і . Розв’язувати краще в умовних координатах t , для цього слід прийняти будь – який рік за умовний.

Відповідні розрахунки виконані у таблиці 4.7 (гр.1-4), підставляючи необхідні дані у рівняння системи (4.3), отримаємо її у вигляді:

, тоді

Підставляючи у рівняння (4.1) значення параметрів і , одержимо:

Підставляючи послідовно значення часу і т.д., одержимо вирівняні значення ряду динаміки (див. гр. 5 табл. 4.7). Представимовихідний і вирівняний ряд на графику (див. рис. 4.1)

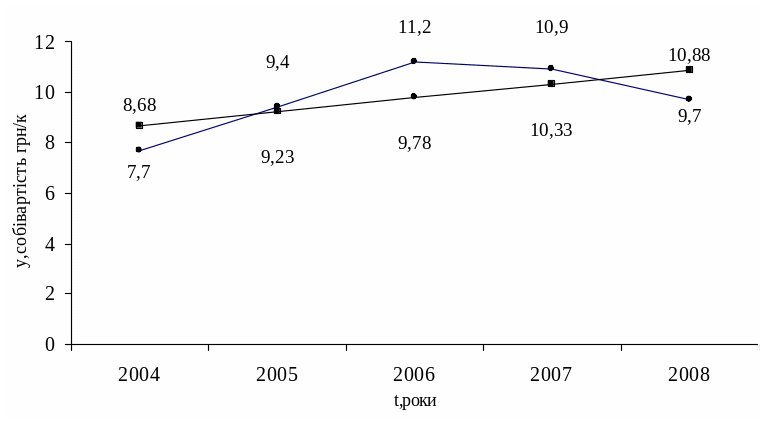
Рисунок 4.1 – Зміна собівартості продукції “А” за роками