4 Методика испытаний. Вариация аллана

Оценка чувствительности микромеханического гироскопа (ММГ) к внешней угловой скорости существенно зависит от решения проблемы выделения информационного сигнала на фоне имеющих место в канале измерения шумовых составляющих. Их структура и характер существенно влияют на достоверность этой оценки.

Классические методы исследования случайных процессов (выборочная дисперсия, спектральная плотность, автокорреляционная функция) не всегда позволяют получить идентификацию источников погрешностей и их количественный вклад в общую статистику шума, особенно в области низких частот.

В последние годы для решения подобных задач применяется метод вариации Аллана, разработанный Давидом Алланом из Американского института стандартов в середине 1960-х г.г. Изначально метод применялся для анализа фазовой и частотной нестабильности прецизионных генераторов.

Позже он был адаптирован для изучения характеристик случайного дрейфа целого ряда датчиков, в том числе, угловой скорости.

Сущность метода вариации Аллана состоит в вычислении дисперсии не самих отклонений центрированного случайного процесса, как это делается при определении классической выборочной дисперсии, а разницы соседних отклонений. Метод оперирует понятием группы последовательных дискретных значений случайной величины U(t), формируемой из массива N измерений. При этом количество используемых при вычислении групп K=N/M, где M – размер группы. Вычисление вариации Аллана состоит в определении дисперсии разницы средних значений двух соседних групп, отстоящих по времени на величину времени осреднения τ=M/f_s, где f_s – частота опроса измеряемой величины, т.е.

(11)

Физически параметр τ представляет собой интервал осреднения измеренных значений в группе размером M.

Вместе с тем существует однозначная связь вариации Аллана с классическими характеристиками случайного процесса в частотной области вида

(12)

где S_U(f) – спектральная плотность выходного сигнала U(t).

Исходя из известных для инерциальных измерителей основных физических причин возникновения шумовых составляющих предлагается аппроксимирующее выражение для в виде

(13)

где R, K, B, N, Q – коэффициенты случайной скорости дрейфа, определяемой как:

• R – коэффициент квазидетерминированного изменения входной скорости вида ω(t)=Rt. Область ошибок датчика, имеющих пропорциональную времени работы ошибку вследствие различных факторов (деградация параметров гироскопа, линейное во времени изменение внешних условий: температура, дрейф основания и др.);

• K – коэффициент случайного блуждания скорости и описываемая спектральная плотность

(14)

• B – коэффициент нестабильности смещения нуля, который связывают с техническими особенностями узлов и компонентов датчика, подверженных фликкер-шуму различной природы: электроника и др. Величина нестабильности (°/ч) получена как минимальное значение σ(τ) на участке кривой Аллана с нулевым наклоном.

Д анная составляющая проявляется на значительных временах усреднения τ, поэтому ее влияние становится важным при измерении углового положения на длительных интервалах времени. И описываемая спектральная плотность вида фликкер-шума ( -шума)

(15)

• N – коэффициент случайного блуждания угла. Численное значение ARW (°/√ч) устанавливается путем построения прямой линии наклоном -1/2 и определения значения СКО в точке τ =1. ARW характеризует скорость нарастания интегрированного сигнала (угла) со временем. И описываемая спектральная плотность (белый шум)

(16)

• Q – коэффициент квантования выходного сигнала определяется цифровой природой измерения гироскопа (характеристики АЦП, измерение смещения фазы на π, 2π и т.д. И описываемая спектральная плотность

(17)

В некоторых случаях аппроксимация может быть дополнена составляющими, описывающими марковский и синусоидальные шумы.

На практике для анализа зависимости от времени осреднения τ (размера группы М) и количественной оценки отдельных составляющих обычно используется построенный в логарифмическом масштабе график изменения квадратного корня от интервала осреднения τ.

В общем случае при использовании вариации Аллана для анализа шумовых составляющих по результатам достаточного объема наблюдений выходного сигнала измерителя проводится построение графика вычисляемой в соответствии с функцией с последующим определением по методу наименьших квадратов значений коэффициентов полинома, обеспечивающих максимальное совпадение экспериментальной и аппроксимирующей функций.

Полученные значения коэффициентов R, K, B, N, Q характеризуют интенсивность отдельных шумовых составляющих выходного сигнала измерителя.

Однако для предварительной количественной оценки составляющих может быть использована тенденция доминирования отдельных составляющих на различных интервалах τ, в характерных наклонах графика , представленного в логарифмическом масштабе. Из выражения (3) следует, что различным шумовым составляющим соответствуют характерные наклоны графика (табл.1).

Таблица 1

Q	N	B	K	R
-1	-1/2	0	+1/2	+1

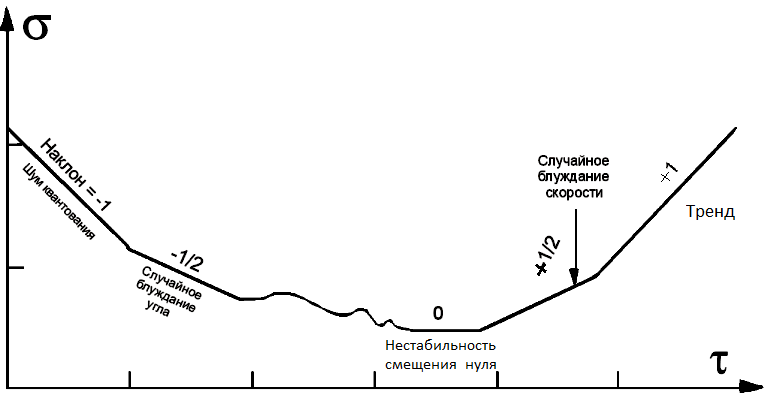
Рис. 6. Различные шумовые составляющие на графике вариации Аллана

При наличии в составе выходного сигнала синусоидальной составляющей вида ω(t)=ω₀ sin(2πf₀ t+Ө) при постоянном значении ω₀, f₀ и случайным значением Ө с равномерной плотностью распределения на интервале 0 ÷ 2π, в выражении (3) появляется плотностью распределения вида

(8)

где ₍₉₎

Эта составляющая, как шум от квантования сигнала, характеризуется средним наклоном графика -1 с наложением затухающих с нарастанием τ колебаний.