3.2 Уравнения динамики чэ

Для оценки количественных соотношений и качественных процессов, происходящих при работе прибора, необходимо исследовать его поведение во времени, для чего необходимо получить его математическую модель. Для вывода уравнений динамики ротора ММГ можно воспользоваться уравнениями Лагранжа второго рода или Эйлера.

Кинематическая схема гироскопа показана на рис.3. При работе ротор гироскопа колеблется относительно оси Z на угол , а выходные колебания ротора в связанных с ним осях определяются углами  и . Ориентация связанных с ротором осей О X_Р Y_Р Z_Р, относительно основания О X Y Z задана тремя углами Эйлера-Крылова по схеме на рисунке 3.б. Будем считать, что конечной инерцией в гироскопе обладает лишь ротор, моменты инерции которого для осей 0X_P, 0Y_P, 0Z_P обозначим через A, B и C.

Абсолютные угловые скорости вращения ротора, образующиеся из абсолютных скоростей вращения основания _X, _Y, _Z и относительных скоростей определяются следующим векторно-матричным уравнением кинематики:

(1)

в котором матрицы элементарных поворотов:

, , .

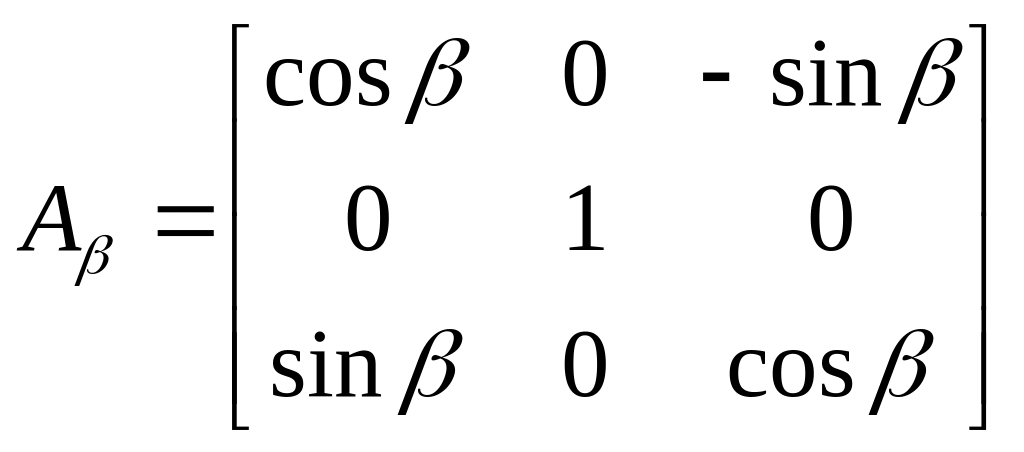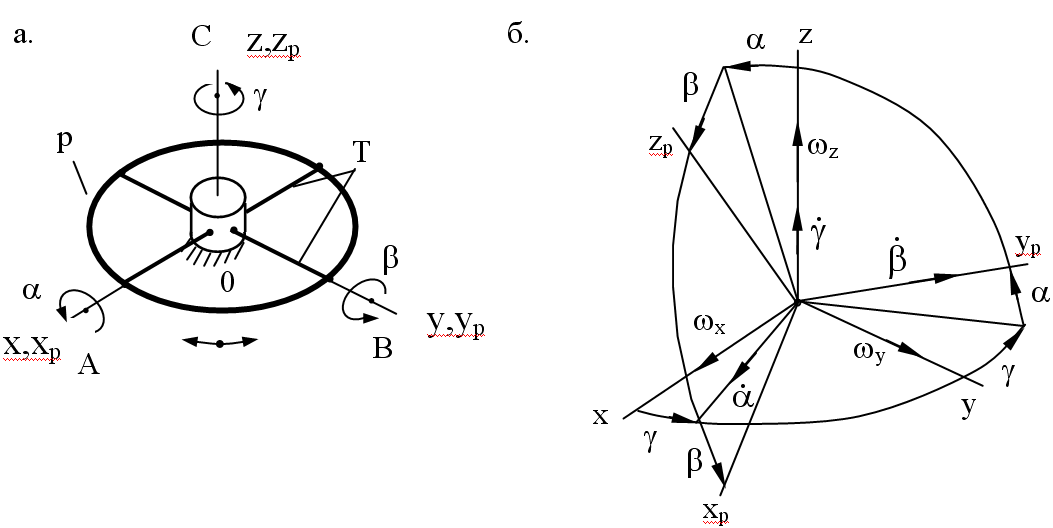
Рис. 3. Кинематическая схема ММГ

При учете в гироскопе лишь одного инерционного тела (ротора), наиболее эффективным путем составления уравнений динамики гироскопа является использование динамических уравнений Эйлера, вытекающих из теоремы об изменении момента количества движения:

(2)

где - момент количества движения ротора, - локальная производная, - вектор угловой скорости вращения ротора, - вектор момента внешних сил в осях ротора.

Момент количества движения ротора определяется как:

(3)

где: А, В, С – главные моменты инерции ротора относительно осей x, y и z соответственно; D, E, F – центробежные моменты инерции ротора.

Кроме того, учтем моменты сил упругости и диссипативные моменты:

(4)

где: m_z – момент, создаваемый двигателем ротора, – жесткость упругого подвеса по осям , – коэффициенты демпфирующих моментов, m_Bzp, m_Byp, m_Bxp – прочие внешние моменты в осях ротора.

Подставляя выражения (1), (3) и (4) в (2) получим искомые уравнения движения ротора в собственных осях. Следует отметить, что полученная система уравнений достаточно громоздка и содержат большое число слагаемых (более 200 в каждом), из-за чего работа с ними сопряжена с рядом сложностей. На практике для дальнейшей работы с уравнениями движения они упрощаются, за счет:

• учета конструктивных параметров ММГ;

• учета желаемых характеристик в режиме датчика угловой скорости;

• заменой , при малых углах;

• заменой , при малых углах;

•   ,   ;

• исключения слагаемых выше второго порядка малости;

• исключения влияния центробежных моментов инерции.

С учетом указанных упрощений уравнения динамики принимают следующий вид:

;

;

. (5)

В системе уравнений (5) центробежно-маятниковые моменты и по сравнению с жесткостями и малы, то же касается соотношения моментов , , и , , к моментам сил инерции , и .

Таким образом, можно сделать два важных вывода:

1. Динамика ротора ММГ относительно осей X, Y и Z близка к динамике колебательных звеньев.

2. Слагаемые и представляют собой моменты гироскопической реакции и являются информационными.