
- •Часть 1 Учебное пособие
- •Введение 4
- •1. Электростатическое поле 5
- •1.17. Электростатическое поле системы заряженных параллельных протяженных проводов 588
- •Введение
- •1. Электростатическое поле
- •1.1. Основные определения
- •1.2. Закон Кулона
- •1.3. Напряженность электрического поля
- •1.4. Электрическое напряжение. Разность электрических потенциалов
- •1.5. Безвихревой характер электростатического поля. Градиент электрического потенциала
- •1.6. Силовые и эквипотенциальные линии
- •1.7. Вектор электрического смещения
- •1.8. Теорема Гаусса. Постулат Максвелла
- •1.9. Уравнения Пуассона и Лапласа
- •1.10. Граничные условия на поверхности проводников
- •1.11. Граничные условия на поверхности раздела двух диэлектриков
- •1.12. Электрическая емкость
- •1.13. Основная задача электростатики
- •1.14. Расчет электростатического поля с помощью теоремы Гаусса и постулата Максвелла
- •1.15. Расчет одномерных электростатических полей по уравнениям Пуассона и Лапласа
- •1.16. Метод зеркальных изображений
- •1.17. Электростатическое поле системы заряженных параллельных протяженных проводов
- •Основная
- •Дополнительная
1.15. Расчет одномерных электростатических полей по уравнениям Пуассона и Лапласа
Электростатическое поле в однородной среде с постоянной диэлектрической проницаемостью полностью характеризуется уравнением Пуассона (1.11) или (если в рассматриваемой области отсутствуют объемные связанные заряды) уравнением Лапласа (1.12).
Наиболее просто уравнения Пуассона и Лапласа решаются в случае одномерных полей, потенциалы которых зависят только от одной координаты. При этом дифференциальные уравнения в частных производных переходят в обыкновенные дифференциальные уравнения второго порядка, решение которых при известных граничных условиях является несложной задачей.
Так, в прямоугольной системе координат уравнения Пуассона и Лапласа для одномерного поля будут иметь следующий вид:
![]() (1.22)
(1.22)
![]() (1.23)
(1.23)
Решение уравнения (1.22), очевидно, может быть получено лишь тогда, когда объемная плотность заряда и абсолютное значение диэлектрической проницаемости заданы как функции координат во всем пространстве. Например, если объемная плотность изменяется вдоль оси ОХ по закону
![]()
(где коэффициент а и показатель степени n являются постоянными), то, в случае, когда =const, частное решение уравнения Пуассона будет иметь следующий вид:
![]() (1.24)
(1.24)
где С1 и С2 - постоянные интегрирования, которые определяются из граничных условий.
В случае, когда объемная плотность заряда также является постоянной величиной, решение имеет вид
![]()
Частное решение уравнения Лапласа (1.29) можно представить следующим образом:
![]() (1.25)
(1.25)
В цилиндрической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят от того, функцией какой координаты является искомый потенциал U. Например, если потенциал U зависит только от радиальной координаты r (U=U(r)), то уравнения (1.11) и (1.12) будут иметь вид
![]() (1.26)
(1.26)
![]()
![]() (1.27)
(1.27)
Решение уравнения (1.26) определяется видом функции . Если, например, объемная плотность заряда изменяется вдоль радиуса r по закону
![]()
то искомое решение будет иметь вид:
![]() (1.28)
(1.28)
Для случая, когда объемная плотность заряда не зависит от координаты r, решение уравнения (1.26) можно представить следующим образом:
![]() (1.29)
(1.29)
Решение уравнения Лапласа (1.27) имеет вид:
![]() (1.30)
(1.30)
Если искомый потенциал является функцией только одной угловой координаты , то уравнения Пуассона и Лапласа приобретают следующий вид:
![]() (1.31)
(1.31)
![]() (1.32)
(1.32)
При постоянном значении уравнение (1.31) имеет частное решение
![]() .
(1.33)
.
(1.33)
Решение уравнение Лапласа (1.32) можно записать следующим образом:
![]() (1.34)
(1.34)
В сферической системе координат для одномерного поля вид уравнения Пуассона или Лапласа и их решение зависят также от того, функцией какой координаты является искомый потенциал U.
Так, если потенциал U зависит только от радиальной координаты r, то уравнения Пуассона и Лапласа будут иметь вид:
![]() (1.35)
(1.35)
![]() (1.36)
(1.36)
При изменении объемной плотности заряда по закону
![]() ,
,
решение уравнения (1.35) можно представить следующим образом:
![]() (1.37)
(1.37)
Если является постоянной величиной, решение будет иметь вид
![]() (1.38)
(1.38)
Уравнение Лапласа (1.36) имеет следующее решение:
![]() (1.39)
(1.39)
В случае, если потенциал U зависит только от одной координаты , уравнение Лапласа (1.12) будет иметь вид
![]() (1.40)
(1.40)
Решение этого уравнения можно представить следующим образом:
![]() (1.41)
(1.41)
Если потенциал U является функцией только одной координаты , то уравнение (1.12) будет иметь вид
![]()
а его решение является линейной функцией этой координаты
Пример 1. Плоский конденсатор с двумя слоями диэлектрика подключен к источнику постоянного напряжения U0=100В (рис. 1.25). Относительные значения диэлектрической проницаемости слоев r1=3, r2=6. Толщина слоев - d1=d2=1мм. Один из слоев заряжен с объемной плотностью , которая изменяется по толщине по закону =10-4х Кл/м3.
Пренебрегая краевым эффектом, найти распределение потенциала и напряженности поля в слоях диэлектрика.
Построить графики изменения потенциала и напряженности электрического поля вдоль оси ОХ.
Решение. Данная задача по расчету электрического поля является одномерной. В первом слое электрический потенциал отвечает уравнению Лапласа (1.23), а во втором - уравнению Пуассона (1.22). Решение этих уравнений можно представить с помощью выражений (1.24) и (1.25) , соответственно, при n=1 и а=1.
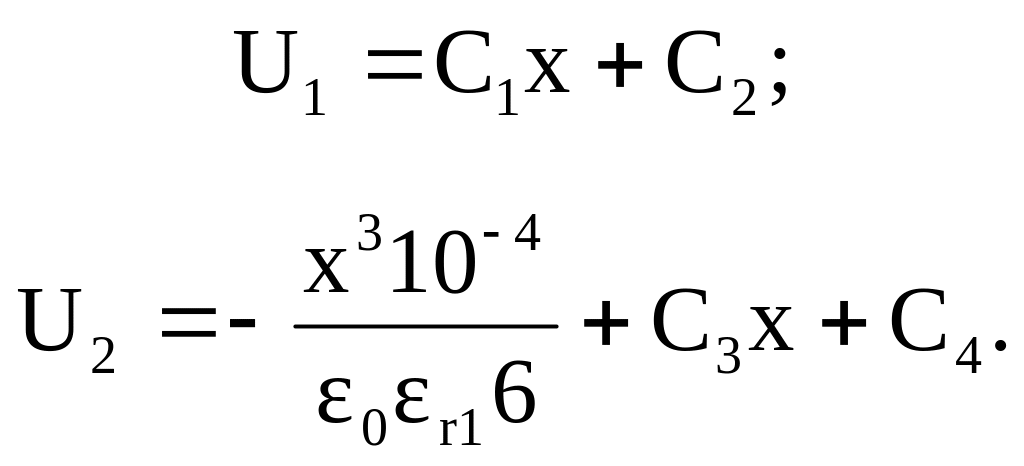
Для определения постоянных интегрирования используем граничные условия на внешних границах области и на границе раздела двух диэлектриков (внутренней границе).
Будем при этом считать, что правая пластина имеет нулевой потенциал.
![]()

Здесь D1 и D2 - нормальные составляющие вектора электрического смещения.
![]()
Из первого равенства следует, что С2=U0.
Перепишем три следующих граничных условия, подставляя в них соответствующие выражения для потенциалов и вектора электрического смещения:
![]()
![]()
![]()
Решая последнюю систему из трех уравнений относительно неизвестных С1, С3, и С4, получим С1=-66670, С3=-33333, С4=66.666.
Таким образом, окончательно выражения для напряженности поля и потенциалов можно записать в виде:
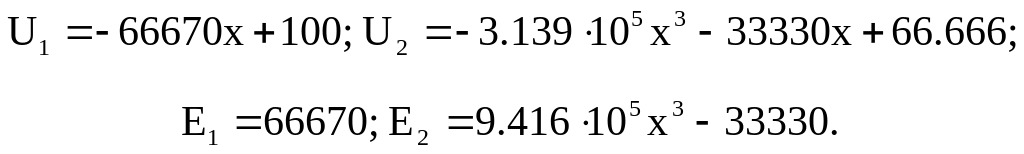
Графики изменения потенциала и напряженности поля представлены на рис. 1.26
Н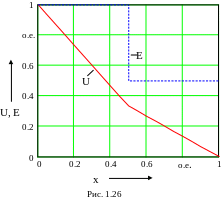 а
графике все значения представлены в
относительных единицах, причем за
базисные значения приняты значения
потенциала и напряженности поля на
поверхности левой пластины (Ub=100
В, Eb=66670
В/м).
а
графике все значения представлены в
относительных единицах, причем за
базисные значения приняты значения
потенциала и напряженности поля на
поверхности левой пластины (Ub=100
В, Eb=66670
В/м).
П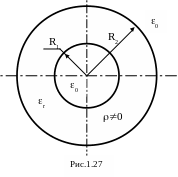 ример
2. Бесконечно длинный диэлектрический
(r=4)
полый цилиндр заряжен и находится в
воздухе. Радиус внутренней поверхности
цилиндра R1=2мм,
наружной - R2=6мм
(рис.1.27). Объемная плотность заряда
является функцией расстояния от оси
цилиндра =0.1r.
ример
2. Бесконечно длинный диэлектрический
(r=4)
полый цилиндр заряжен и находится в
воздухе. Радиус внутренней поверхности
цилиндра R1=2мм,
наружной - R2=6мм
(рис.1.27). Объемная плотность заряда
является функцией расстояния от оси
цилиндра =0.1r.
Найти законы изменения потенциала и напряженности поля в функции расстояния от оси цилиндра. Построить графики изменения указанных функций вдоль радиуса.
Решение. Поле в данном случае является одномерным, поскольку напряженность поля и потенциал зависят только от одной радиальной координаты.
При решении задачи по расчету электрического поля в заданной области, эту область необходимо разбить на три подобласти. В первой из них (0rR1) поле отсутствует (Е=0). Во второй подобласти (R1rR2) электрический потенциал отвечает уравнению Пуассона (1.26), а в третьей (R2 r) - уравнению Лапласа (1.27), которые имеют решения (1.28) (при n=1,a=0.1) и (1.30).
Перепишем эти решения в следующем виде:
![]()
Здесь индексы у потенциалов обозначают их принадлежность ко второй и третьей подобластям.
Постоянные интегрирования определим из граничных условий, которые можно поставить как из классических граничных условий, так и из следующих соображений. Поскольку поле внутри цилиндра отсутствует, то при r=R1, можно принять Е2=0.
![]()
Отсюда сразу определяем постоянную С1=7.533.
Примем потенциал равным нулю на наружной поверхности цилиндра (U2=0 при r=R2), тогда
![]() (1.42)
(1.42)
и, таким образом, С2=106.335.
Потенциал U3 со стороны третьей подобласти на этой же поверхности (r=R2) также будет равен нулю.
![]()
Здесь же на границе раздела двух диэлектриков равны между собой нормальные составляющие векторов электрического смещения, а с учетом того, что в нашем случае вектор электрического смещения имеет одну составляющую, которая направлена по радиусу, то это означает, что на границе раздела равны между собой и сами векторы электрического смещения.
![]()
Перепишем последнее уравнение в следующем виде:
![]() (1.43)
(1.43)
Решая совместно уравнения (1.42) и (1.43), находим постоянные интегрирования С3=-783.427, С4=-4008.
Таким образом, выражения для напряженности электрического поля и потенциала принимают вид
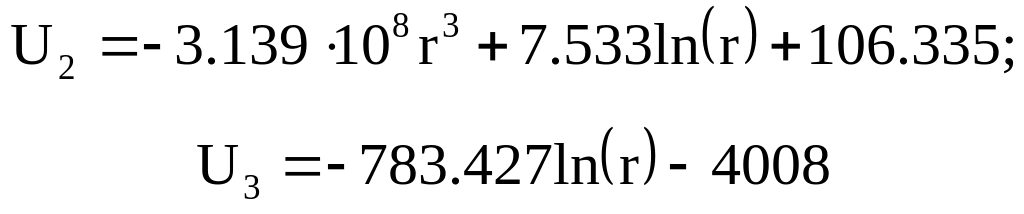
![]()
Потенциал в первой подобласти (внутри цилиндра) является величиной постоянной, равной значению потенциала со стороны второй подобласти на внутренней поверхности цилиндра.
График изменения потенциала и напряженности электрического поля представлен на рис. 1.28. Все значения на графике даны в относительных единицах. За базисное значение напряженности поля принято ее значение на наружной поверхности цилиндра Eb=130.6кВ/м.
В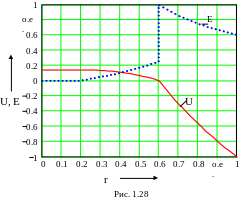 качестве базисного значения потенциала
принято абсолютное значение потенциала
на расстоянии 0.01м от оси цилиндра
Ub=400.2В.
качестве базисного значения потенциала
принято абсолютное значение потенциала
на расстоянии 0.01м от оси цилиндра
Ub=400.2В.
Это же расстояние r=0.01м принято за базисное значение радиальной координаты.
Пример 3. Цилиндрический бесконечно длинный конденсатор заполнен двухслойным диэлектриком, относительные значения диэлектрической проницаемости слоев которого равны соответственно r1=2 и r2=4. Радиус внутренней жилы равен R1=1мм, внутренний радиус наружной обкладки - R3=4мм, радиус поверхности раздела слоев диэлектрика - R2=2мм (рис. 1.29). К обкладкам конденсатора приложено постоянное напряжение Uо = 100 В. Один из диэлектриков заряжен (внутренний). Объемная плотность заряда является функцией расстояния r от оси конденсатора =аr2 (а=10).
Определить закон изменения потенциала и напряженности электрического поля в каждом слое.
Построить графики изменения напряженности поля и потенциала вдоль радиуса.
Решение. В данной задаче поле так же является одномерным. Поэтому электрический потенциал в первом слое диэлектрика (R1rR2) удовлетворяет уравнению (1.26), а во втором слое (R2rR3) - уравнению (1.27). Эти уравнения имеют решения (1.28) и (1.30), соответственно. Перепишем их (при n=2) в следующем виде:
![]()
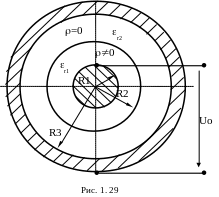
Для определения постоянных интегрирования С1, С2, С3, С4 поставим граничные условия.
Так, если принять потенциал наружного электрода равным нулю, то потенциал внутреннего электрода будет равен U0.
![]() ;
(1.44)
;
(1.44)
![]() .
(1.45)
.
(1.45)
На границе раздела слоев диэлектриков (r=R2) равны между собой потенциалы и векторы электрического смещения (вектор электрического смещения имеет одну составляющую, направленную вдоль радиуса).
![]()
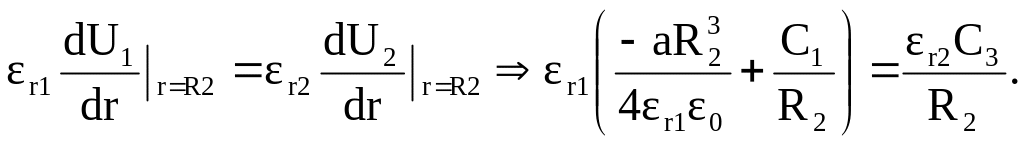
Решая систему уравнений, составленную из последних двух уравнений и уравнений (1.44) и (1.45) относительно постоянных интегрирования, получаем С1=-94.917, С2=-555.628, С3=-48.588, С4=-268.279.
Таким образом, выражения для напряженности электрического поля и потенциала принимают вид
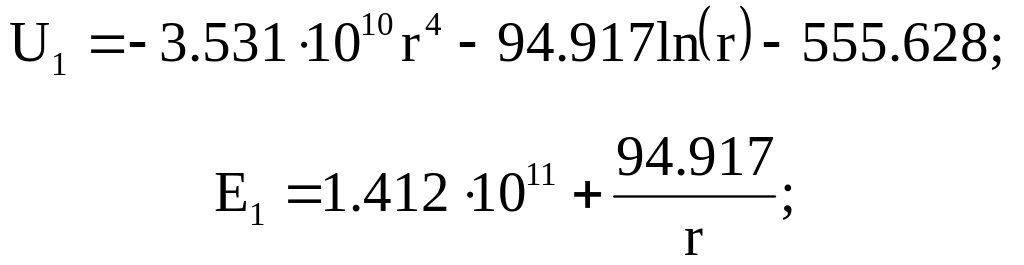
![]()
Графики изменения данных функций вдоль радиуса представлены на рис. 1.30.
В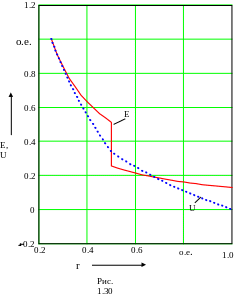 се
значения на графике даны в относительных
единицах. За базисное значение
напряженности поля и потенциала приняты
их значения на поверхности внутреннего
электрода Eb=95.06кВ/м,
Ub=100В.
За базисное значение радиальной
координаты принят внутренний радиус
наружного электрода R2.
се
значения на графике даны в относительных
единицах. За базисное значение
напряженности поля и потенциала приняты
их значения на поверхности внутреннего
электрода Eb=95.06кВ/м,
Ub=100В.
За базисное значение радиальной
координаты принят внутренний радиус
наружного электрода R2.
Пример 4. Две протяженные проводящие пластины расположены в воздухе под углом 0=/4 друг к другу и не соприкасаются (рис. 1.31). Напряжение между пластинами U0=100В.
Пренебрегая краевым эффектом, определить закон распределения потенциала и напряженности электрического поля между пластинами.
Поле между пластинами является одномерным (все величины зависят только от одной угловой координаты цилиндрической системы координат). Потенциал, в этом случае, удовлетворяет уравнению (1.32) с решением (1.34).
Постоянные интегрирования определяются из граничных условий
![]()
или
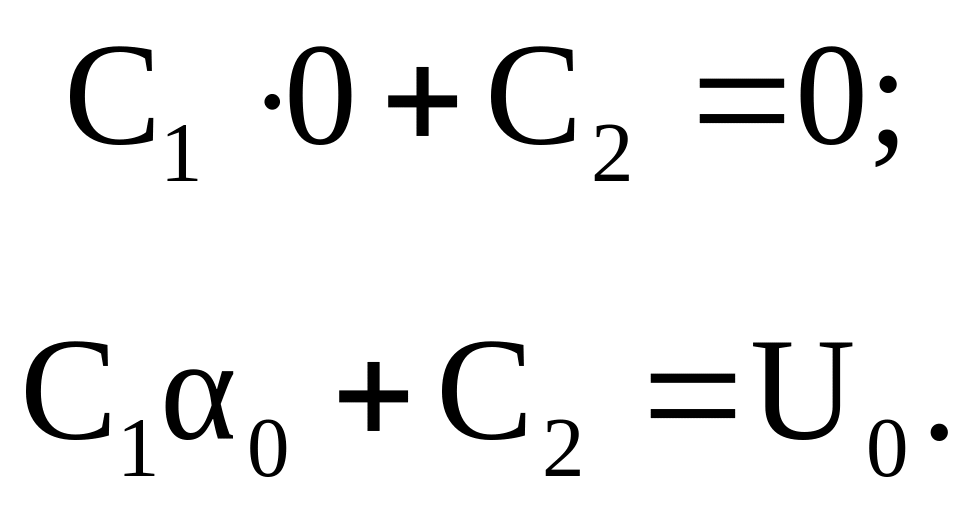
Из данной системы уравнений определяем постоянные интегрирования С2=0, С1=U0/0.
Таким образом, закон изменения искомых функций вдоль угловой координаты цилиндрической системы координат можно окончательно представить следующим образом:
![]()
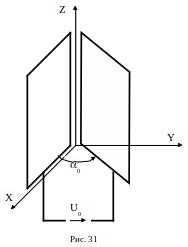
Как видно из последних выражений, эквипотенциальными поверхностями являются полуплоскости, проходящие через ось OZ и изолированными драг от друга, а линиями поля являются дуги окружностей с центром в начале координат.
Пример 5. Шар из диэлектрика (r = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: = k×r (k = 0,05). Радиус шара R = 2см. Рассчитать потенциал и напряженность электрического поля внутри и вне шара.
Данная задача была решена в примере 3 раздела 1.14 с помощью теоремы Гаусса.
Покажем, что этой же цели можно добиться и путем решения уравнений Пуассона (1.35) и Лапласа (1.36), которым удовлетворяет потенциал поля внутри и вне шара, соответственно.
Выражения, определяющие этот потенциал внутри (1.37) и вне шара (1.39), можно для данного случая представить в следующем виде:
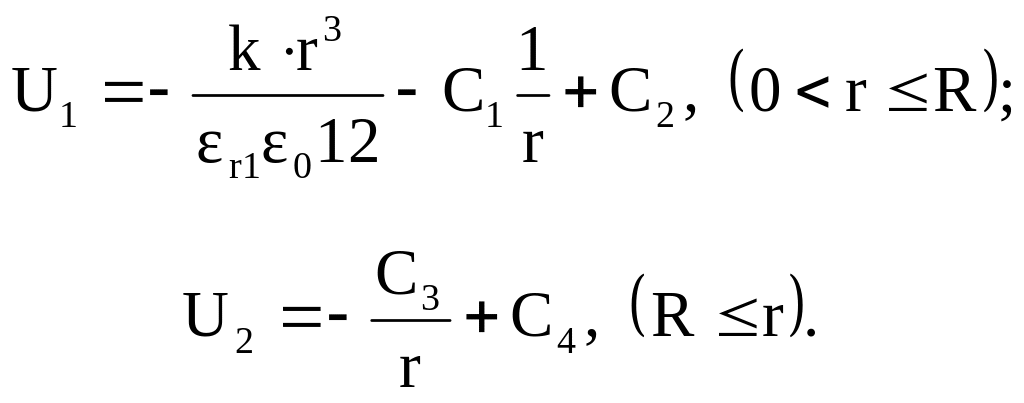
Постоянные интегрирования определяются из известных граничных условий и с помощью некоторых физических соображений. Так, потенциал в центре шара (r=0) имеет конечное значение, поэтому постоянную С1 необходимо принимать равной нулю (С1=0). Далее, принимая потенциал равный нулю в точке, лежащей в бесконечности (r=), получаем С4=0.
Оставшиеся две постоянные С2 и С3 определяем исходя из того, что на поверхности шара (r=R) равны между собой потенциалы и нормальные составляющие вектора электрического смещения
![]()
Перепишем данные граничные условия в следующем виде:
![]()
Решая совместно последние уравнения, находим постоянные интегрирования. C2=38460, С3=-709,964.
Подставляя значения этих постоянных в формулы для потенциалов, получаем
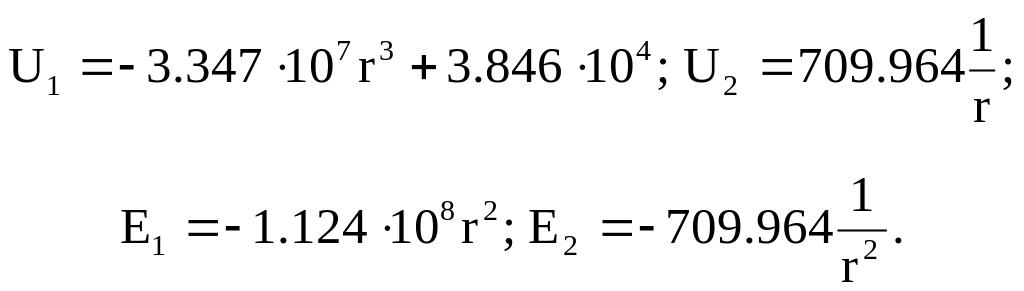 Отсюда
видно, что данные выражения полностью
аналогичны тем, которые были получены
в примере 3 предыдущего раздела.
Отсюда
видно, что данные выражения полностью
аналогичны тем, которые были получены
в примере 3 предыдущего раздела.
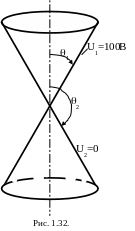
Пример 6. Две тонкие проводящие поверхности в виде коаксиальных конусов с изолированными вершинами расположены в воздухе. Потенциал первой поверхности U1=0, второй - U2=100В (рис. 1.32), 1=/6, 2=2/3.
Найти закон распределения потенциалов и напряженности электрического поля в пространстве между конусами.
Данная задача является одномерной, поскольку, в силу симметрии, решение для потенциала U зависит только от угла . Поле в данном случае характеризуется уравнением (1.40) и имеет решение (1.41).
Исходя из заданных граничных условий составим уравнения для нахождения постоянных интегрирования С1 и С2
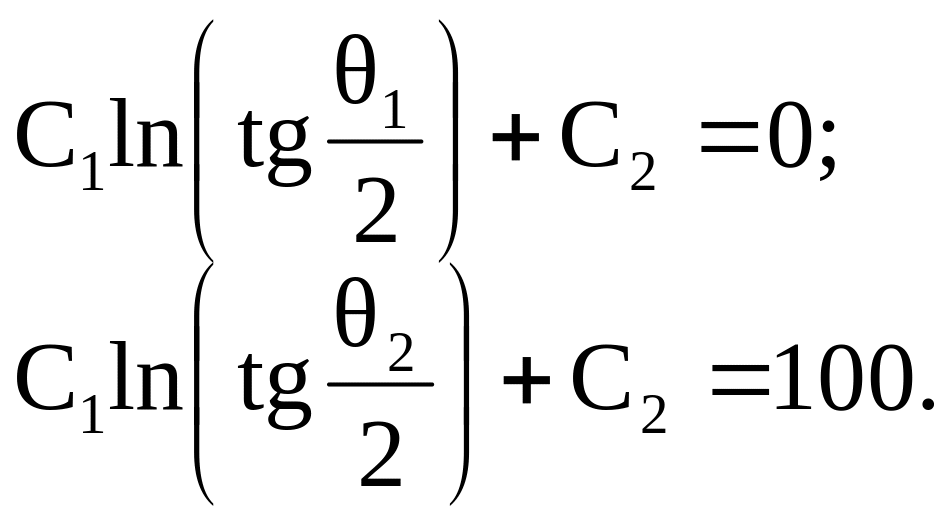
Р ешая
данную систему, получим С1=53.583,
С2=70.567.
ешая
данную систему, получим С1=53.583,
С2=70.567.
Таким образом, выражение для определения потенциала будет иметь вид
![]()
Напряженность электрического поля имеет одну составляющую
![]()
Э квипотенциальными
поверхностями являются поверхности
конусов с изолированными вершинами.
При =/2
один из конусов переходит в плоскость.
Линии поля лежат на меридианах.
квипотенциальными
поверхностями являются поверхности
конусов с изолированными вершинами.
При =/2
один из конусов переходит в плоскость.
Линии поля лежат на меридианах.
