1.12. Электрическая емкость

Электрическая емкость характеризует способность тела или системы тел накапливать электрические заряды, запасая таким образом энергию электрического поля.

Емкость определяют как отношение заряда уединенного проводящего тела к его потенциалу(при условии, что точка, в которой потенциал принимается равным нулю, лежит в бесконечности):

С = q/U,

а емкость двух проводящих тел, разделенных диэлектриком и заряженных равными по значению и противоположными по знаку зарядами - как отношение абсолютного значения заряда к разности потенциалов этих тел:

С=q/(U₁ - U₂). (1.15)

Емкость зависит от геометрических размеров, конфигурации, диэлектрической проницаемости диэлектрика и взаимного расположения тел.

Емкость измеряется в Фарадах (Ф).

Ниже приведены выражения для емкостей простейших систем.

Емкость плоского конденсатора с однослойным диэлектриком равна:

С = (S)/d,

где S - площадь каждой пластины; d - расстояние между пластинами.

Емкость плоского конденсатора с двухслойным диэлектриком с диэлектрической проницаемостью ₁ и ₂ каждого слоя и их толщиной, равной d₁ и d₂ определяется выражением

. (1.16)

Емкость на единицу длины цилиндрического конденсатора (коаксиального кабеля) с однослойным диэлектриком и радиусами обкладок R₁ и R₂ (R₁R₂):

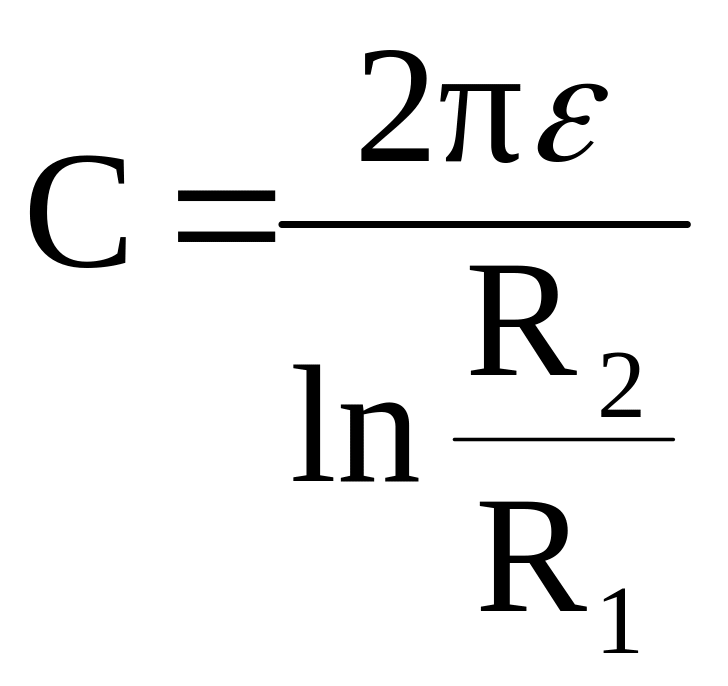. (1.17)

Емкость сферического конденсатора с наружным радиусом внутренней сферической обкладки R₁ и внутренним радиусом внешней сферической обкладки R₂ определяется выражением

. (1.18)

Емкость уединенного шара радиусом R равна:

С = 4R. (1.19)

Емкость двух шаров радиусами R₁ и R₂, расположенных на расстоянии D (геометрические и электрические оси совпадают)

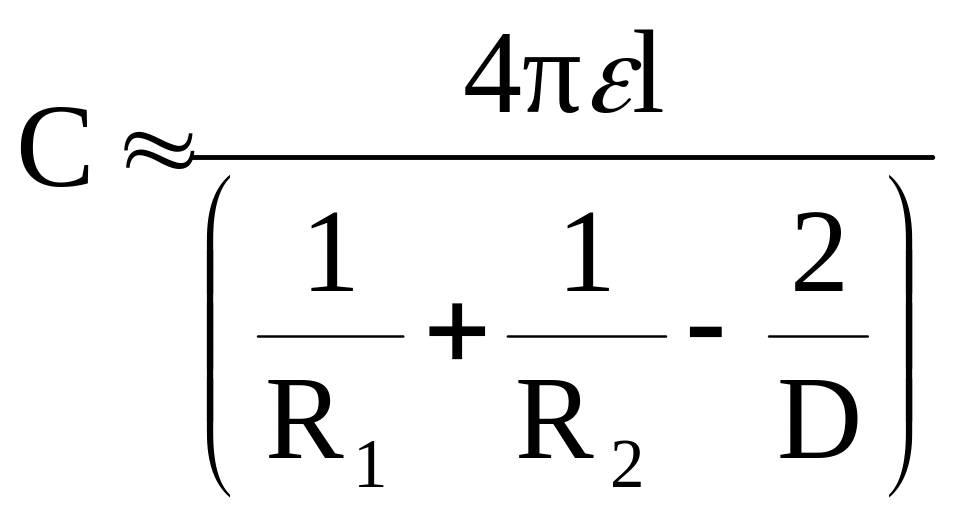. (1.20)

Емкость уединенного цилиндра радиусом R и длиной l:

.

Если длина цилиндра много больше его радиуса (l>>R), то емкость можно определять по приближенной формуле

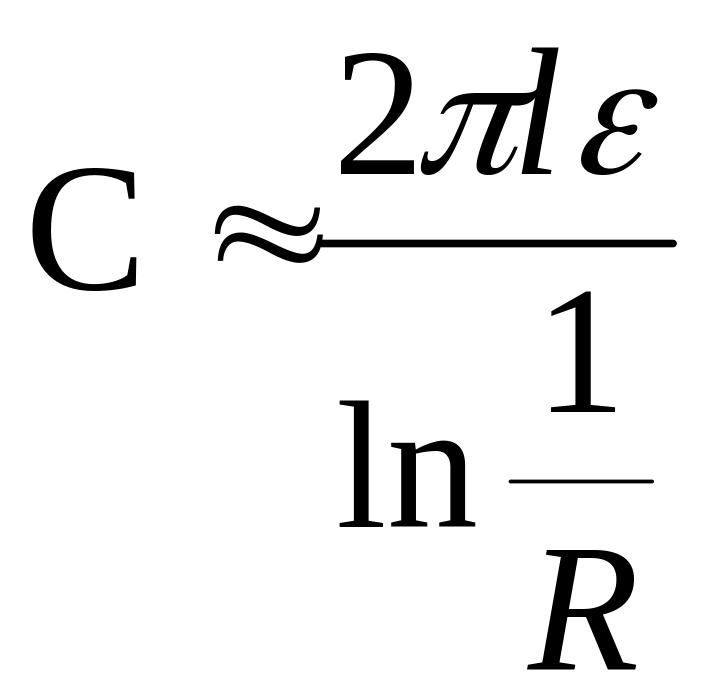. (1.21)

При наличии нескольких заряженных проводников вводят понятие частичных емкостей и эквивалентной емкости системы.

Частичной емкостью называется емкость между двумя проводниками, входящими в систему проводников. Частичную емкость между двумя проводниками определяют как абсолютное отношение заряда одного проводника к разности потенциалов между этими проводниками, когда остальные проводники системы имеют один и тот же потенциал.

Эквивалентная емкость (рабочая) - емкость между двумя проводниками, входящими в систему проводников, учитывающая частичные емкости между парой проводов системы.

1.13. Основная задача электростатики

Общей задачей расчета электростатического поля является определение напряженности поля во всех его точках по заданным зарядам или потенциалам тел. Для электростатического поля задача полностью решается отысканием потенциала как функции координат. Обратная задача отыскания распределения зарядов по заданному распределению зарядов решается с помощь уравнения Пуассона или с помощь уравнения Лапласа и граничного условия у поверхности заряженных проводящих тел. Это наиболее простой тип задач. Однако большей частью задача оказывается значительно сложнее. Обычно рассматривается система заряженных проводящих тел с известной геометрией, окруженных диэлектриком, в котором отсутствуют объемные заряды. Заданы либо потенциалы тел, либо полные заряды. Распределение же зарядов по поверхности каждого тела неизвестно и подлежит определению. В этом и заключается основная трудность задачи. Также неизвестным является и распределение потенциала в пространстве. Особенно усложняется задача для неоднородной или неизотропной среды.

Задачи можно решать аналитически или графически, либо путем моделирования.

В простых случаях задачи на аналитический расчет решают путем использования теоремы Гаусса в интегральной форме. В более сложных приходится решать уравнение Лапласа (или Пуассона, если задан закон распределения свободных зарядов).

Ниже рассмотрено несколько простых примеров решения задачи по расчету электростатического поля аналитическими методами.