1.9. Уравнения Пуассона и Лапласа

Уравнения Пуассона и Лапласа являются основными дифференциальными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме. Действительно, подставляя в уравнение

вместо величин Е_х; Е_у; Е_z их выражения через потенциал:

получаем уравнение

Это дифференциальное уравнение носит название уравнения Пуассона.

Интеграл

является решением уравнения Пуассона для случая, когда заряды распределены в конечной области пространства.

Если в рассматриваемой области пространства отсутствуют объемные электрические заряды, то уравнение Пуассона получает вид

и называется в этом частном случае уравнением Лапласа.

Отметим, что в цилиндрической и сферической системах координат уравнение Пуассона и Лапласа имеют другую форму записи. Поэтому данные уравнения часто записывают в виде, не зависящем от системы координат:

²U = -; (1.11)

²U = 0. (1.12)

Оператор ² часто обозначают и называют оператором Лапласа или лапласианом.

При интегрировании уравнения Лапласа (или Пуассона) в решение входят постоянные интегрирования. Их определяют из граничных условий.

1.10. Граничные условия на поверхности проводников

В проводящем теле, находящемся в электростатическом поле, все точки тела имеют одинаковый потенциал, поверхность проводящего тела является эквипотенциальной поверхностью и линии напряженности поля в диэлектрике нормальны к ней. Обозначив через Е_n и Е_t нормальную и касательную к поверхности проводника, составляющие вектора напряженности поля в диэлектрике около поверхности проводника, указанные условия можно записать в виде:

Е_t = 0; Е = Е_n = -U/n; D = -U/n = ,

где  - поверхностная плотность электрического заряда на поверхности проводника.

Таким образом, на границе раздела проводящего тела и диэлектрика отсутствует касательная к поверхности (тангенциальная) составляющая напряженности электрического поля, а вектор электрического смещения в любой точке, непосредственно примыкающей к поверхности проводящего тела численно равен плотности электрического заряда  на поверхности проводника.

1.11. Граничные условия на поверхности раздела двух диэлектриков

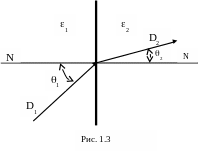
На поверхности раздела двух диэлектриков с различными абсолютными диэлектрическими проницаемостями ₁ и ₂ (рис. 1.3) равны между собой касательные составляющие напряженности поля

(1.13)

и нормальные составляющие вектора электрического смещения

(1.14)

Здесь индекс 1 относится к первому диэлектрику, а индекс 2 – ко второму.

Условия (1.13) и (1.14) можно представить и в таком виде

и .

Из данных граничных условий можно получить еще одно условие - условие преломления линий поля при переходе их из одного диэлектрика в другой:

,

где ₁ и ₂ - углы между вектором напряженности (или смещения) и нормалями к границе раздела сред. При этом, если вектор напряженности перпендикулярен к границе раздела, то электрическое смещение не меняется при переходе из одной среды в другую, а напряженность поля меняется скачком.

При переходе через границу раздела двух диэлектриков электрический потенциал не претерпевает скачков.