1.6. Силовые и эквипотенциальные линии

Электростатическое поле можно характеризовать совокупностью силовых и эквипотенциальных линий. Силовая линия – это мысленно проведенная в поле линия, начинающаяся на положительно заряженном теле и оканчивающаяся на отрицательно заряженном теле. Проводится она таким образом, что касательная к ней в любой точке ее дает направление напряженности в этой точке.

В электростатическом поле могут быть проведены эквипотенциальные поверхности. Под эквипотенциальной поверхностью понимают совокупность точек поля, имеющих один и тот же потенциал. Если мысленно рассечь электростатическое поле какой-либо секущей плоскостью, то в полученном сечении будут следы пересечения плоскости с эквипотенциальными поверхностями. Их называют эквипотенциальными линиями.

Эквипотенциальные и силовые линии в любой точке поля пересекаются под прямым углом.

1.7. Вектор электрического смещения

Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды. Учитывают поляризацию с помощью вектора поляризации , который для анизотропных и однородных сред выражается через напряженность поля следующим образом: , где  - диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = _связ ). Кроме этого, при анализе электростатических полей используют вектор электрического смещения:

. (1.8)

Единицей электрического смещения является кулон на метр квадратный (Кл/м²).

Величина  = ₀ +  является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение _r = /₀ называют относительной диэлектрической проницаемостью.

1.8. Теорема Гаусса. Постулат Максвелла

Вначале рассмотрим понятие потока вектора через поверхность. Пусть в электростатическом поле есть некоторый элемент поверхности, площадь которого численно равна ds. Выберем положительное направление нормали (перпендикуляра) к элементу поверхности. Вектор в некотором масштабе (рис. 1.2) равен площади элемента ds, а его направление совпадает с положительным направлением нормали.

Б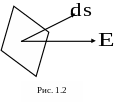 удем полагать, что площадь элемента достаточно мала, чтобы в пределах этого элемента вектор можно было считать одним и тем же во всех точках. Тогда поток вектора через элемент поверхности определится скалярным произведением

Если поверхность S, через которую определяется поток вектора велика, то этот поток определяется с помощью интеграла по поверхности.

Теорема Гаусса формулируется следующим образом: поток вектора напряженности электрического поля сквозь замкнутую поверхность в однородном изотропном диэлектрике равен отношению электрического заряда, заключенного внутри этой поверхности, к диэлектрической проницаемости диэлектрика.

Математическое выражение теоремы Гаусса в интегральной форме имеет вид

. (1.9)

Для любой среды справедлива обобщенная теорема Гаусса или постулат Максвелла:

. (1.10)

Теорема Гаусса и постулат Максвелла в дифференциальной форме записи имеют вид:

или в иной форме:

,

где  -объемная плотность электрического заряда в данной точке пространства. Выражение, стоящее в левой части уравнения, называется расхождением или дивергенцией вектора напряженности или электрического смещения.

Выражение для дивергенции в различных системах координат имеет различную форму записи. Так, в декартовой системе координат она имеет следующий вид:

,

здесь Е_х; Е_у; Е_z – проекции вектора на соответствующие оси координат.