1.4. Электрическое напряжение. Разность электрических потенциалов

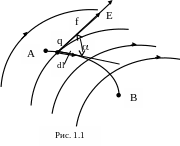
Если частица с зарядом q переносится в электрическом поле вдоль некоторого пути, то действующие на нее силы поля совершают работу. Отношение этой работы к переносимому заряду представляет физическую величину, называемую электрическим напряжением. При перемещении частицы по пути dl (рис. 1.1) силы поля совершают работу

Через обозначен вектор, равный по величине элементу пути dl и направленный по касательной к пути в сторону перемещения заряженной частицы. Угол  есть угол между векторами и .

Работа, совершаемая силами поля при перемещении частицы вдоль всего пути от точки А до точки В (рис. 1.1), равна

Она пропорциональна линейному интегралу напряженности поля вдоль заданного пути. Этот линейный интеграл равен электрическому напряжению вдоль заданного пути от А до В. Принято обозначать напряжение буквой u. Таким образом,

Следовательно,

Таким образом, электрическое напряжение представляет собой физическую величину, характеризующую электрическое поле вдоль рассматриваемого пути и равную линейному интегралу напряженности электрического поля вдоль этого пути.

Единицей напряжения является вольт (В).

Из сказанного вытекает, что значение напряженности электрического поля равно падению напряжения, отнесенного к единице длины линии напряженности поля.

Рассмотрим теперь величины, именуемые электрическим потенциалом и разностью электрических потенциалов.

В электростатическом поле линейный интеграл напряженности поля по любому замкнутому контуру равен нулю:

(1.3)

или в дифференциальной форме

, (1.4)

где l - контур интегрирования. Величина, стоящая в левой части последнего уравнения, называется вихрем или ротором.

Это важное свойство электростатического поля вытекает из принципа сохранения энергии.

Условие (1.3) или (1.4) говорит о том, что в электростатическом поле линейный интеграл от вектора напряженности поля, взятый от любой точки А до любой точки В, не зависит от выбора пути интегрирования и полностью определяется в заданном поле положением точек А и В. Это обстоятельство позволяет ввести понятие о потенциале электростатического поля. Потенциал электростатического поля в точке А определяется как линейный интеграл вектора , взятый от точки А до некоторой точки Р

. (1.5)

Потенциал в точке Р равен нулю.

Линейный интеграл вектора напряженности поля вдоль некоторого пути от точки А до точки В есть разность потенциалов в точках А и В:

. (1.6)

1.5. Безвихревой характер электростатического поля. Градиент электрического потенциала

Условие (1.4) свидетельствует, что электростатическое поле имеет безвихревой характер. Поле, удовлетворяющее этому условию, называют безвихревым.

Электрический потенциал, с учетом условия (1.4), может быть связан с вектором напряженности электрического поля при помощи следующего соотношения:

. (1.7)

Градиент потенциала равен приращению потенциала, отнесенному к единице длины и взятому в направлении, в котором это приращение имеет наибольшее значение.

Формы представления градиента в различных системах координат различны. В декартовой системе координат его записывают так:

,

здесь  - дифференциальный оператор Гамильтона (оператор набла).

Оператор Гамильтона применяют для сокращения записи различных операций над функциями, в том числе и операцию взятия градиента.

Таким образом, равенство (1.7) может быть записано в форме

Знак минус в этом равенстве (и эквивалентном ему равенстве (1.7)) указывает, что потенциал убывает в направлении линий напряженности поля.

Сказанное свидетельствует о том, что всякое безвихревое поле есть поле потенциальное, то есть такое, которое может быть охарактеризовано потенциальной функцией U.

Обратно, всякое потенциальное поле является безвихревым.