1. Электростатическое поле

1.1. Основные определения

Электрическим полем называют одну из сторон электромагнитного поля, характеризующуюся воздействием на электрически заряженную частицу с силой, пропорциональной заряду частицы и не зависящей от ее скорости.

Электростатическое поле – это частный вид электрического поля. Оно создается совокупностью электрических зарядов, неподвижных в пространстве (по отношению к наблюдателю) и неизменных во времени.

Электрический заряд является одной из основных характеристик частиц и тел, определяющей их взаимодействие с внешним электромагнитным полем, а также их взаимосвязь с собственным электромагнитным полем.

Существует наименьший электрический заряд, который называется элементарным электрическим зарядом (заряд протона и электрона).

Электрический заряд бывает положительным и отрицательным.

Под электрическим зарядом тела понимают скалярную величину, равную алгебраической сумме элементарных электрических зарядов в этом теле.

При рассмотрении поля в веществе различают свободные заряды и связанные заряды.

Единицей электрического заряда является (в СИ) кулон (Кл).

Взаимодействие между неподвижными электрическими зарядами описывается законом Кулона.

1.2. Закон Кулона

Если два точечных заряда q₁ и q₂ расположены в пустоте, то сила взаимодействия между ними, согласно опытному закону Кулона, равна

,

где - единичный вектор, направленный по линии, соединяющей заряды; = 8,85×10^-12 Ф/м (фарада на метр) - электрическая постоянная; r - расстояние между зарядами.

Эта сила направлена по линии, соединяющей точечные заряды. Заряды, имеющие одинаковые знаки, стремятся оттолкнуться друг от друга, а заряды противоположных знаков – сблизиться.

Под точечными зарядами понимают следующее: линейные размеры тел, на которых расположены взаимодействующие заряды, много меньше расстояния между телами.

1.3. Напряженность электрического поля

Главной физической величиной, характеризующей электрическое поле, является напряженность электрического поля.

Напряженность электрического поля есть векторная величина, равная пределу отношения силы , с которой электрическое поле действует на неподвижное точечное положительно заряженное тело, внесенное в рассматриваемую точку поля, к заряду этого тела q₀, когда этот заряд стремится к нулю, и имеющая направление, совпадающее с направлением силы:

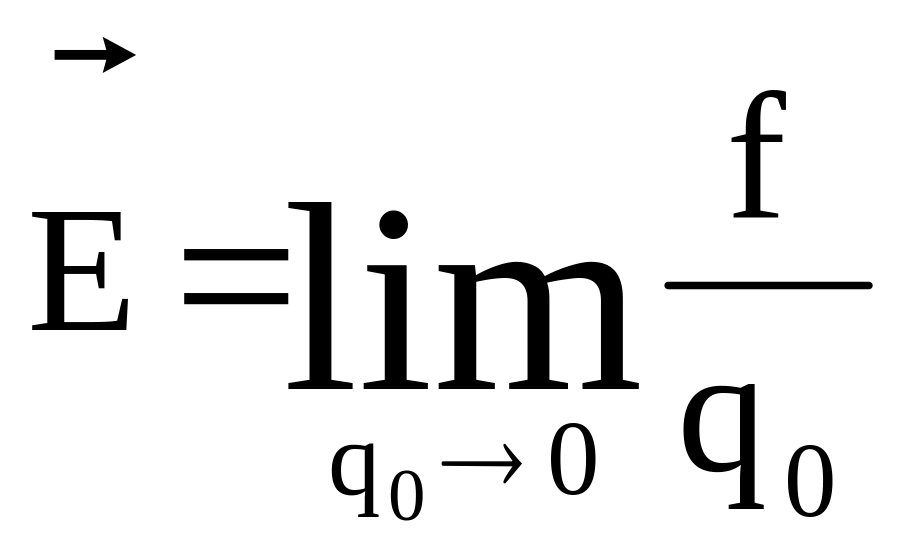. (1.1)

Единицей измерения напряженности поля является вольт на метр (В/м).

Из выражения (1.1) следует, что сила , действующая на конечной величины точечный заряд q, внесенный в поле, будет равна .

Из закона Кулона следует выражение для напряженности электрического поля точечного заряда q, расположенного в пустоте

. (1.2)

Здесь единичный вектор направлен от заряда q в точку наблюдения; r - расстояние от заряда до точки наблюдения.

Если поле создается несколькими зарядами (q₁, q₂, q₃, …), то его напряженность равна геометрической сумме напряженностей от каждого из зарядов в отдельности:

то есть при расчете электростатического поля применим метод наложения.