Методичекские указания к курсовому проекту по дисциплине «моделирование транспортных процессов» на тему «автоматизированное решение транспортой задачи линейного программирования» Содержание

Введение	3
2. Транспортная задача линейного программирования	5
2.1. Сущность транспортной задачи линейного программирования	5
2.2. Алгоритм решения транспортной задачи методом потенциалов	7
2.3. Решение транспортной задачи линейного программирования с помощью надстройки «Поиск решения» в MS Excel	18
2.4. Оптимизация загрузки производственных мощностей предприятий по производству запасных частей для автомобильно-дорожного транспорта	23
2.5. Исходные данные	28
2.6. Последовательность решения задачи………………………………	30
Заключение	33
Список использованных источников	34

Введение

Важной проблемой управления предприятиями в сложных условиях рынка является своевременное принятие правильных решений в связи с изменениями в экономической ситуации. Одним из путей решением этой проблемы является применение методов экономико-математического моделирования в управление предприятиями, в т.ч. автомобильном транспорте.

Математические модели и методы, являющиеся необходимым элементом в современной экономической науке, как на микро- , так и на макроуровне, изучаются в таких ее разделах, как математическая экономика и эконометрика.

Эконометрика- это раздел экономической науки, который изучает количественные закономерности в экономике при помощи корреляционно-регрессивного анализа и широко применяется при планировании и прогнозировании экономических процессов в условиях рынка.

Математическая экономика занимается разработкой, анализом и поиском решений математических моделей экономических процессов, среди которых выделяют макро- и микроэкономические классы моделей.

Макроэкономические модели изучают экономику в целом, опираясь на такие укрупнённые показатели, как валовый национальный продукт, потребление, инвестиции, занятость и т.д. При моделировании рыночной экономики особое место в этом классе занимают модели равновесия иэкономического роста.

Равновесные модели описывают такие состояния экономики, когда результирующая всех сил, стремящихся вывести её из некоторого состояния, равна нулю ( модель"затраты-выпуск" В.Леонтьева и модель Эрроу-Дебре ).

Модели экономического роста описывают экономическую динамику и приводят к поиску и анализу траекторий стационарного роста (модель Харрода-Домара, модель Солоу, модели магистрального типа ).

Микроэкономические модели описывают экономические процессы на уровне предприятий и фирм, помогая решать стратегические и оперативные вопросы планирования и оптимального управления в рыночных условиях. Важное место среди микроэкономических моделей занимают оптимизационные модели (задачи распределения ресурсов и финансирования, транспортная задача, максимизация прибыли фирмы, оптимальное проектирование).

В курсовом проекте рассмотрены основные принципы математического моделирования на микроэкономическом уровне и реализация этих принципов на примере классической оптимизационной модели, используемой в экономике транспорта - транспортной задаче.

2. Транспортная задача линейного программирования

2.1. Сущность транспортной задачи линейного программирования

В различных местах оправки имеется однородный груз, который требуется доставить в несколько пунктов назначения. Известно, сколько груза отправляется из каждого пункта и сколько груза должно поступить в пункт назначения. Причём безразлично, какой именно отправитель будет доставлять груз тому или иному получателю. Требуется так организовать перевозки, чтобы обеспечить минимальный общий пробег груза, т. е. минимизировать затраты на транспортировку. Экономико-мате­ма­тическая модель транспортной задачи представляется обычно в виде транспортной таблицы или матрицы.

Таблица 2.1 ­- Экономико-математическая модель транспортной задачи

Примечание. А_i – название пункта отправления; В_j – название пункта назначения; a_i – производственная мощность поставщиков; b_j – спрос потребителей; m – число поставщиков; n – число потребителей; i – номер строки (i-й поставщик) i = 1…m; j – номер столбца (j-й потребитель) j = 1…n; c_ij – показатель критерия оптимальности, удельные затраты на транспортировку единицы продукции (себестоимость перевозок) от поставщика i до потребителя j; x_ij – количество продукции, перевозимое от поставщика i до потребителя j, план перевозок, распределение поставок, корреспонденция грузов.

Условия задачи в принятых обозначениях следующие.

1. Каждый поставщик должен дать ровно столько продукции, столько у него есть, т. е. сумма поставок по каждой строке должна будет равна мощности a_i этой строки:

. (2.1)

2. Каждый потребитель должен получить ровно столько продукции, сколько ему требуется, т. е. сумма поставок по каждому столбцу должна будет равна спросу b_i этого столбца:

. (2.2)

3. Из вышеприведённых условий (2.1) и (2.2) следует:

. (2.3)

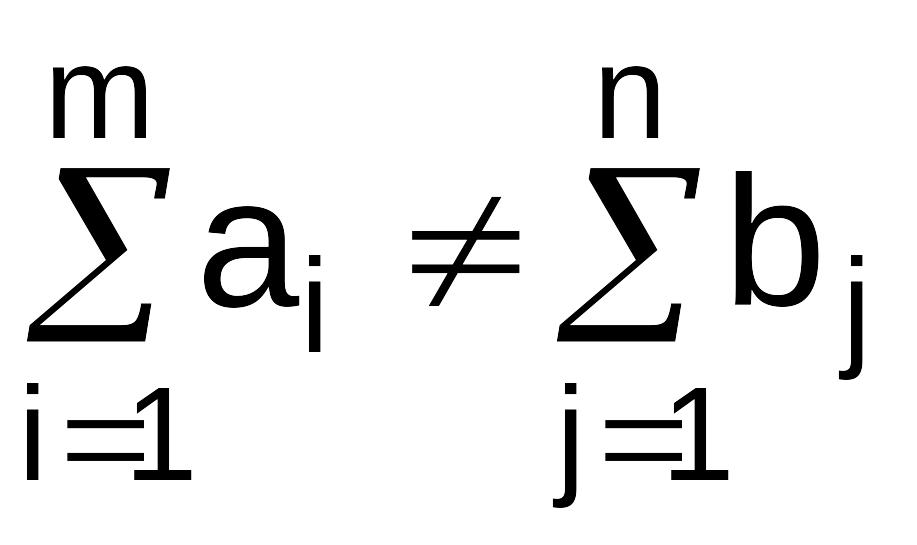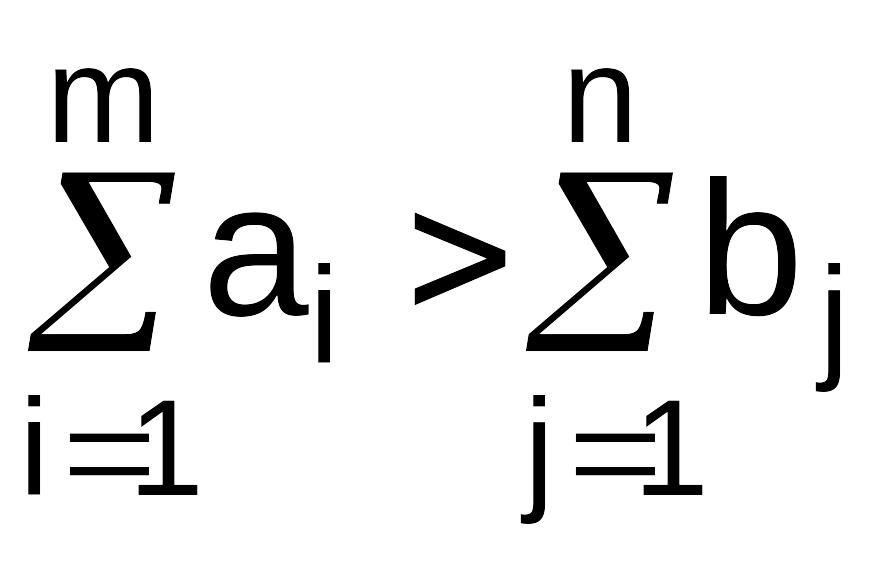В случае если , то транспортная задача линейного программирования называется открытой. Если , то это несбалансированная задача с дефицитом. Если , то это несбалансированная задача с избытком.

Чтобы определить суммарные затраты на перевозки, достаточно просуммировать произведения объёмов каждой поставки на соответствующие им удельные затраты на транспортировку. План будет оптимальным, если эта сумма (целевая функция F) будет сведена к минимуму:

. (2.4)

Транспортная задача является закрытой, если соблюдается условие (2.3). Если данное условие не соблюдается, то для приведения открытой транспортной задачи к закрытому виду вводится фиктивный потребитель ФВ или фиктивный поставщик ФА. Разница между производственной мощностью и спросом относится на его счёт. Расходы по доставке груза до фиктивного потребителя или фиктивного поставщика равны нулю, так как груз фактически не перевозится.