
- •3) Тв системы летательных аппаратов. Назначение и классификация
- •Биллет № 14
- •1) Оптимальная линейная фильтрация с позиции максимума отношения сигнала к помехе. Согласованный фильтр. Синтез согласованных фильтров.
- •2) Выделение границ (контуров) объектов наблюдения в полутоновых и бинарных изображениях
- •3) Цифровой видеосигнал высокой четкости. Особенности аналого-цифрового преобразования
- •Билет №15
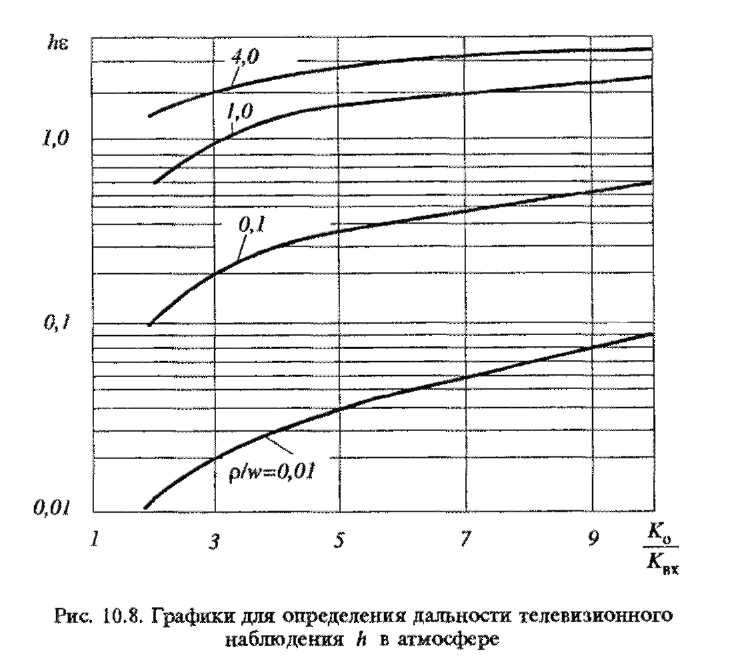
- •1) Дальность действия тв системы наблюдения в атмосфере.
- •2) Обнаружение сигналов на фоне гауссовых шумов.
- •3) Ввод данных в режиме прерывания. Способы идентификации источника прерывания (при наличии нескольких видеодатчиков)
Билет №15
Системы прикладного телевидения
1) Дальность действия тв системы наблюдения в атмосфере.
При использовании телевизионной
аппаратуры для наблюдения за объектами,
находящимися вне помещений, необходимо
учитывать влияние атмосферы на
дальность наблюдения. При определении
дальности наблюдения за удаленными
объектами следует иметь в виду, что,
во-первых, происходит ослабление
лучистой энергии воздушной средой и,
во-вторых, снижается контраст
изображения объекта на входе системы.
Снижение контраста обусловлено
рассеивающим свойством атмосферы и,
как правило, является определяющим
дальность наблюдения h.
Контраст на входе системы наблюдения равен

Или т.к.


где
 —
контраст объекта с фоном;
—
контраст объекта с фоном;
 — яркость объекта или фона (большее
значение);
— яркость объекта или фона (большее
значение);
 — яркость насыщенного слоя атмосферы
(яркость неба у горизонта); р — коэффициент
отражения объекта или фона; w
— коэффициент погоды;
— яркость насыщенного слоя атмосферы
(яркость неба у горизонта); р — коэффициент
отражения объекта или фона; w
— коэффициент погоды;
 — показатель ослабления лучистого
потока слоем атмосферы толщиной 1
км; Е— освещенность объекта и фона.
— показатель ослабления лучистого
потока слоем атмосферы толщиной 1
км; Е— освещенность объекта и фона.
Коэффициентом погоды w называется отношение яркости неба у горизонта к яркости горизонтальной абсолютно белой поверхности, освещенной суммарным дневным светом. Коэффициент погоды зависит от метеорологических условий и может быть как меньше, так и больше единицы.
Из второго уравнения находим искомую дальность наблюдения:

На рис. представлены расчетные графики для определения дальности наблюдения.
Теоретические основы преобразования информации в оптико электронных системах (ТОПИ):
2) Обнаружение сигналов на фоне гауссовых шумов.
Условные вероятности ошибок
![]()
где yi - случайные величины, распределенные по закону Гаусса с нулевым средним значением
![]()
где yi- случайные величины, распределенные по закону Гаусса и со средним значением Si.
Т.
к.
 независимых
гауссовых величин является
также гауссовой со средним значением
и дисперсией, равными
сумме средних и сумме дисперсий слагаемых,
независимых
гауссовых величин является
также гауссовой со средним значением
и дисперсией, равными
сумме средних и сумме дисперсий слагаемых,
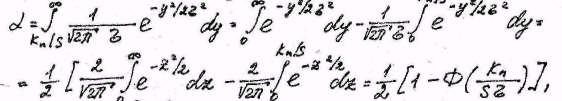
где![]() -
интеграл вероятностей.
-
интеграл вероятностей.
Условную вероятность ошибки первого рода:
В![]() еличина
еличина
 отношение сигнала к шуму потоку (или
по напряжению).
отношение сигнала к шуму потоку (или
по напряжению).
Условная вероятность ошибки второго рода (вероятность пропуска сигнала)
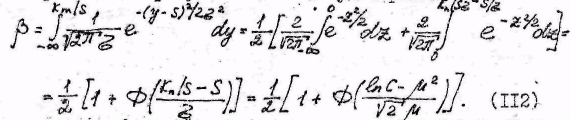
При использовании критерия максимума правдоподобия величина С=1 и тогда условные вероятности ошибок
![]()
Н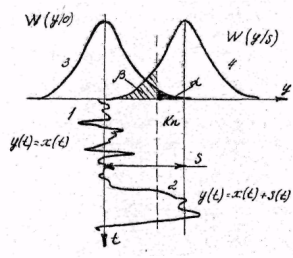 а
рис. случайные процессы с нулевым средним
значением (кривая 1) и со средним, равным
S
(кривая 2), а также функции распределения
этих процессов (кривые 3 и 4); условные
вероятности ошибок обнаружения α и β.
Важные характеристики: зависимости
Д1=1-β=f(α)при
различных значениях величины отношения
сигнала к шуму μ
а
рис. случайные процессы с нулевым средним
значением (кривая 1) и со средним, равным
S
(кривая 2), а также функции распределения
этих процессов (кривые 3 и 4); условные
вероятности ошибок обнаружения α и β.
Важные характеристики: зависимости
Д1=1-β=f(α)при
различных значениях величины отношения
сигнала к шуму μ
"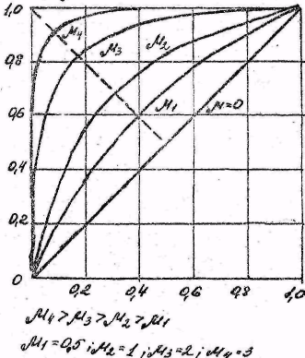 На
рис приведено семейство кривых 1-β=f(α)
для
нескольких значений μ (пунктир
соответствует случаю, когда
.используется критерий максимума
правдоподобия).
На
рис приведено семейство кривых 1-β=f(α)
для
нескольких значений μ (пунктир
соответствует случаю, когда
.используется критерий максимума
правдоподобия).
Представленное семейство кривых называется рабочей характеристикой приемника обнаружения. Рабочие характеристики приемника позволяют при заданных величинах α и β оперативно определять вероятность правильного обнаружения.
Норма ошибок (полная безусловная вероятность ошибки)
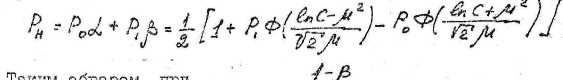
 помощью кривой решения
можно задавшись допустимым
значением нормы ошибок (Рн=
Рндоп)
найти
требуемую величину отношения
сигнал/шум. При
обнаружении
детерминированного сигнала
на фоне гауссова шума
величина отношения сигнал/шум
определяет
норму ошибок (максимум
сигнала к шуму м.б. использован в качестве
критерия качества обнаружения).
помощью кривой решения
можно задавшись допустимым
значением нормы ошибок (Рн=
Рндоп)
найти
требуемую величину отношения
сигнал/шум. При
обнаружении
детерминированного сигнала
на фоне гауссова шума
величина отношения сигнал/шум
определяет
норму ошибок (максимум
сигнала к шуму м.б. использован в качестве
критерия качества обнаружения).
Автоматизированные видеоинформационные системы
