- •Тематика практических занятий
- •Список лабораторных работ
- •1. Некоторые астрономические величины Радиус Земли. . . . . . . . . . . . . . . . . ………………… . . .6,37·106 м
- •2. Плотность твердых тел и жидкостей (Мг/м3, или г/см3)
- •Алюминий. . . . . . . . . . . . . . . . . . . . . .2.70 Висмут. . . . . . . . . . . . . . . . . . . . . . .9,80
- •Никель. . . . . . . . . . . . . . . . . . . . . . .8,80
- •3. Плотность газов при нормальных условиях (кг/м3)
- •4. Упругие постоянные твердых тел (округленные значения)
- •5. Эффективный диаметр молекул, динамическая вязкость и теплопроводность газов при нормальных условиях
- •6. Критические параметры и поправки Ван-дер-Ваальса
- •8. Поверхностное натяжение жидкостей при 20 °с (мН/м)
- •9. Скорость звука с, м/с
- •10. Основные физические постоянные
- •11. Диэлектрическая проницаемость
- •13. Работа выхода электронов из металла
- •432700, Ульяновск, пл. 100-летия в.И. Ленина, 4.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ
ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
имени И. Н. УЛЬЯНОВА
ФИЗИКА
(электричество)
МЕТОДИЧЕСКОЕ ПОСОБИЕ ДЛЯ СТУДЕНТОВ-ЗАОЧНИКОВ
СПЕЦИАЛЬНОСТИ «ТЕХНОЛОГИЯ И ПРЕДПРИНИМАТЕЛЬСТВО» ПЕДАГОГИЧЕСКИХ ВЫСШИХ УЧЕБНЫХ ЗАВЕДЕНИЙ

УЛЬЯНОВСК – 2007
Печатается по решению
редакционно-издательского
совета УлГПУ
УДК 530(07)
Зиновьев А.А., Кокин В.А., Кокина И.А.
Физика (электричество). Методическое пособие для студентов-заочников специальности «технология и предпринимательство» педагогических высших учебных заведений. - Ульяновск: УлГПУ имени И.Н.Ульянова, 2007. – 80 с.
Методическое пособие составлено в соответствии с учебным планом и учебной программой по физике для заочного отделения факультета «Технология и предпринимательство». В данной работе даны пояснения к программе курса физики, приведены основные сведения по изучаемым разделам, методические указания по выполнению контрольных работ, приведены примеры решения задач по разделу электромагнетизм.
Ответственный редактор: Кокин В.А., доцент кафедры МПФ.
Рецензент: Чекулаева М.Е., доцент кафедры методики
преподавания физики, к.п.н.
© Ульяновский ордена "Знак Почета" государственный
педагогический университет им. И.Н. Ульянова, 2007.
ПРЕДИСЛОВИЕ
Цель настоящего учебно-методического пособия – оказать помощь студентам-заочникам специальности "Технология и предпринимательство" высших учебных заведений в изучении курса общей физики.
Курс физики на специальности "Технология и предпринимательство" изучается в течение трех семестров: во 2-м семестре изучаются разделы - механика и молекулярная физика; в 3-м семестре - электродинамика и магнетизм; в 4-м - квантовая физика. По учебному плану каждого семестра предусмотрены лекции, практические занятия (обсуждение теоретических вопросов и решение задач), лабораторные работы.
После краткого курса лекций и выполнения лабораторных работ выставляется зачет, после дальнейшей самостоятельной проработки теоретического материала и выполнения контрольной работы выставляется при собеседовании зачет по контрольной работе и принимается устный экзамен. Номер варианта контрольной работы определяется последней цифрой номера зачетной книжки. Прорабатывать теоретические вопросы и решать контрольную работу рекомендуется непосредственно в процессе изучения данного раздела на учебной сессии для получения оперативной консультации, своевременной и успешной сдачи контрольной работы.
При выполнении контрольной работы необходимо придерживаться общих правил (алгоритма решения задач):
- условие задачи переписывать полностью;
на страницах оставлять поля для замечаний преподавателя;
при записи условия в краткой форме выполнить перевод величин в единицы СИ;
решение задач сопровождать пояснениями с использованием рисунка;
решать задачу в общем виде (выразить искомую величину в буквенных обозначениях величин, данных в условии задачи, без промежуточных вычислений);
перед вычислением искомой величины определить ее размерность и убедиться в правильности решения задачи;
на собеседовании по контрольной работе студент должен быть готов дать пояснения по существу решения задач, входящих в его контрольную работу;
к повторному рецензированию контрольной работы незачтенные задачи решать в той же тетради.
титульный лист: контрольная работа должна иметь титульный лист в соответствии с рисунком. Если контрольная работа выполняется в ученической тетради, то на обложку наклеить титульный лист.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
УЛЬЯНОВСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ имени И. Н. УЛЬЯНОВА
Кафедра методики преподавания физики
Ф И З И К А
КОНТРОЛЬНАЯ РАБОТА №___
ВАРИАНТ № ____
Студент гр. Тп – ____ _____________________ (ФИО) № зачетной книжки: _________ Сдано для проверки______________ (дата)
Получено для проверки ______________ (дата) Преподаватель_________________
|
При подготовке к экзамену необходимо ознакомиться с вопросами к экзамену, использовать лекции и рекомендуемую литературу. Каждый билет содержит два теоретических вопроса и задачу. При ответе на теоретический вопрос обратить внимание на осознанное понимание используемых терминов, физических величин, на формулировку законов, применение законов при объяснении наблюдаемых явлений, процессов, на краткое описание эксперимента, подтверждающего данный закон.
РАБОЧАЯ ПРОГРАММА КУРСА ОБЩЕЙ ФИЗИКИ (электричество) ДЛЯ СПЕЦИАЛЬНОСТИ "ТЕХНОЛОГИЯ И ПРЕДПРИНИМАТЕЛЬСТВО" ЗАОЧНЫХ ОТДЕЛЕНИЙ ПЕДАГОГИЧЕСКИХ ВУЗОВ.
Электростатика. Закон сохранения заряда. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Электрический диполь. Силовые линии и поток вектора напряженности электрического поля. Работа сил электрического поля. Циркуляция вектора напряженности электрического поля. Потенциальная энергия и потенциал. Эквипотенциальные поверхности. Теорема Гаусса в вакууме и ее применения для расчета электрических полей. Поляризация диэлектриков. Напряженность электрического поля и электрическая индукция в диэлектрике. Сегнетоэлектрики. Проводники в электростатическом поле. Электроемкость. Конденсаторы. Энергия электрического поля. 8 Постоянный электрический ток. Закон Ома в дифференциальной и интегральной формах. Электродвижущая сила. Классическая теория электропроводности металлов. Закон Джоуля – Ленца. Правила Кирхгофа. Магнитное поле постоянного тока. Основные характеристики магнитного поля. Закон Био-Савара-Лапласа и его применения для расчета магнитных полей прямого и кругового токов. Закон Ампера. Движение заряженных частиц в электрическом и магнитном полях. Эффект Холла. Закон полного тока. Магнитное поле в веществе. Намагниченность. Диамагнетики и парамагнетики. Ферромагнетики.
Электромагнитная индукция. Закон электромагнитной индукции. Правило Ленца. Принцип действия генератора ЭДС. Индуктивность. Явление самоиндукции. Явление взаимной индукции. Трансформатор.
Основы теории Максвелла для электромагнитного поля. Вихревое электрическое поле. Ток смещения. Система уравнений.
Электромагнитные колебания и волны. Колебательный контур. Уравнения колебаний. Формула Томсона. Уравнения электромагнитных волн. Графическое изображение. Законы распространения электромагнитных волн.
Тематика лекций:
Электростатика. Электризация. Электрические заряды. Закон сохранения электрического заряда. Закон Кулона. Электрическое поле. Напряжённость, потенциал электрического поля. Теорема Остроградского-Гаусса. Электроёмкость. Конденсаторы. Энергия электрического поля. Постоянный электрический ток. Электрический ток. Сила тока. Электродвижущая сила источника. Напряжение. Закон Ома для участка цепи. Сопротивление. Зависимость сопротивления от температуры. Правило Кирхгофа для разветвленной цепи. Ток в разных средах. Работа электрического тока.
Магнитные явления. Магнитное поле и его характеристики. Взаимодействия токов. Закон Био-Савара-Лапласа. Магнитное поле прямолинейного проводника с током, кругового тока. Вектор магнитной индукции. Силы, действующие на проводник с током в магнитном поле. Закон Ампера. Силы, действующие на движущий заряд в магнитном поле – сила Лоренца. Магнитные свойства веществ.
Электромагнитная индукция. Опыты Фарадея. Закон электромагнитной индукции – закон Фарадея. Самоиндукция. Индуктивность. Генератор переменного тока. Электрическая цепь переменного тока. Работа и мощность переменного тока. Электромагнитные колебания и волны. Свободные электромагнитные колебания. Колебательный контур. Формула Томсона. Незатухающие колебания. Генератор незатухающих электромагнитных колебаний.
Тематика практических занятий
Электростатика. Закон Кулона. Электрическое поле. Напряжённость и потенциал поля. Электроёмкость, конденсаторы.
Электрический ток. Законы Ома. Законы Кирхгофа.
Электрический ток в разных средах.
Магнитное поле и его характеристики. Электромагнитная индукция. Переменный ток.
Список лабораторных работ
Определение ёмкости конденсатора.
Измерение сопротивлений.
Измерение ЭДС гальванического элемента методом компенсации.
Изучение электронно-лучевого осциллографа
Определение горизонтальной составляющей магнитного поля Земли с помощью тангенс-гальванометра.
Определение длины электромагнитной волны с помощью системы Лехера.
Список вопросов к экзаменам по электродинамике и магнетизму
Электризация. Электрические заряды. Виды электризации тел.
Различие веществ по электрическим свойствам.
Закон сохранения электрического заряда. Понятие замкнутой системы. Экспериментальное подтверждение данного закона.
Закон Кулона.
Электрическое поле. Характеристики электрического поля.
Графическое изображение электрического поля. Напряжённость и потенциал поля точечного заряда.
Однородное поле. Диполь. Принцип суперпозиции полей.
Поток напряжённости. Теорема Остроградского-Гаусса.
Энергия электрического поля.
Проводники и диэлектрики в электрическом поле.
Электроёмкость. Конденсатор. Энергия заряженного конденсатора.
Электрический ток. Условия возникновения электрического тока.
Закон Ома для участка цепи. Сопротивление. Соединение резисторов.
Зависимость сопротивления резисторов от температуры. Полупроводники.
Источники тока. Электродвижущая сила источника
Закон Ома для полной цепи.
Правила Кирхгофа для разветвленной цепи.
Электрический ток в различных средах.
Работа электрического тока. Закон Джоуля-Ленца.
Химическое действие тока. Закон Фарадея для электролиза.
Магнитное поле и его характеристики.
Магнитное поле тока (проводника, кольца, соленоида).
Магнитные свойства вещества. Различия веществ по магнитным свойствам.
Закон Био-Савара-Лапласа.
Сила Лоренца.
Сила Ампера.
Принцип действия электродвигателя.
Электромагнитная индукция. Опыты Фарадея.
Закон электромагнитной индукции (Фарадея).
Закон Ленца.
Идеи Максвелла при излучении электромагнитных явлений.
Явления самоиндукции. Индуктивность.
Генератор переменного тока. Параметры тока.
Электрическая цепь переменного тока с элементами омического, индуктивного и ёмкостного сопротивления.
Полное сопротивление простейшей цепи переменного тока.
Работа и мощность переменного тока.
Электромагнитные колебания. Колебательный контур.
Свободные электромагнитные колебания. Уравнение колебаний.
Незатухающие электромагнитные колебания. Генератор электромагнитных колебаний.
Принцип радиосвязи.
Примечание. Экзаменационный билет содержит два теоретических вопроса (по электродинамике и магнетизму) и качественную задачу.
Теоретический материал
Электростатика. Тема 1.
§ 1 – 1. Электрический заряд
Электричество как особый вид материи изучалось еще древними греками, но количественная мера его - электрический заряд – была введена лишь после опытов Кулона. Основным свойством заряда является его дискретность. Наименьший заряд, известный в настоящее время, равен 1,6·10 –19 Кулона (единица измерения – Кулон - будет определена позднее). Предполагается, что возможны дробные части этого заряда – кварки, но они до настоящего времени экспериментально не обнаружены. Однако, установлено, что суммарная величина электрического заряда в доступной нашим наблюдениями части Вселенной остается постоянной. Это положение носит название закона сохранения заряда.
Существуют два различных типа электрических зарядов, один из которых по предложению Б.Франклина был назван положительным, а другой – отрицательным. Субъективный характер выбора такого названия привел к тому, что заряд электрона – наиболее известной элементарной частицы – оказался отрицательным. Это, в свою очередь, привело к некоторой путанице в определении направления электрического тока, но на первой стадии изучения электричества нас будут интересовать неподвижные заряды, обычно называемые статическими.
§ 1 – 2. Закон Кулона
Еще из школьного курса физики известно, что электрические заряды взаимодействуют друг с другом. Величина силы взаимодействия измерена Кулоном, и закон, характеризующий силу взаимодействия двух статических точечных зарядов Q и q, носит его имя. Если учесть, что сила – это вектор, то этот закон может быть записан в таком виде:

где
 – единичный вектор, направленный вдоль
прямой, соединяющей оба заряда, расстояние
между которыми равно r.
– единичный вектор, направленный вдоль
прямой, соединяющей оба заряда, расстояние
между которыми равно r.
Коэффициент k вводится в связи с использованием определенной системы единиц. В принятой у нас системе (СИ) этот коэффициент выражается через так называемую диэлектрическую постоянную вакуума ε0 = 8,86 ·10 –12 Ф/м (k = 1/ 4π ε0). Причиной появления этого коэффициента является выбор единицы измерения заряда – в СИ заряд измеряется в Кулонах, являющихся производными единицами (основной единицей служит Ампер – единица измерения силы тока).
Замечание: понятие точечного заряда является математической абстракцией, в действительности приходится иметь дело с зарядами, заполняющими либо некоторый объем, либо некоторую площадь, а иногда – в случае тонких длинных проводов – некоторую длину. Как правило, заряды распределяются неравномерно, поэтому можно рассматривать объемную, поверхностную или линейную плотности зарядов, определяемые как:
 ;
;
 ;
;

где dV, dS и dl – бесконечно малые элементы объема, площади и длины соответственно. Величина бесконечно малого заряда, который можно рассматривать как точечный, при этом определяется как dq1= ρdV, dq2 = σdS, dq3 = τdl.
§ 1 – 3. Напряженность электрического поля
В предыдущем разделе (механике) отмечалось, что любое взаимодействие тел, находящихся на некотором расстоянии друг от друга, осуществляется посредством поля. Применительно к электрическим зарядам это означает, что вокруг любого заряда существует особый вид материи – электрическое поле. Это поле не воспринимается непосредственно чувствами человека. Для обнаружения поля используются другие заряды, называемые пробными. Однако, из закона Кулона следует, что величина силы воздействия на пробный заряд зависит от величины этого заряда. Для характеристики самого поля вводится величина силы, действующей на пробный заряд, отнесенная к величине этого пробного заряда. Эта величина называется напряженностью электрического поля. Другими словами можно сказать, что напряженность электрического поля есть сила, действующая на единичный положительный заряд, помещенный в данную точку поля. Если обозначить заряд, поле которого мы изучаем – Q, то напряженность поля в любой точке пространства вокруг этого заряда, находящейся на расстоянии r от него, равна:
 ;
;

Напряженность поля от нескольких зарядов находится по принципу суперпозиции: напряженность поля от суммы зарядов равна сумме всех напряженностей от каждого заряда в отдельности, т.е. E (Σ Qi) = Σ (Ei).
Этот принцип позволяет находить напряженность поля от любых зарядов, распределенных в пространстве, причем, вместо суммы используются интегралы. Однако вычисление осложняются тем, что напряженность поля – вектор. Поэтому часто приходится сначала вычислять отдельные составляющие вектора Е, а общую величину находить их суммированием. Для прямоугольной системы координат это делается сравнительно просто:
E2 = Ex2 + Ey2 +Ez2.
П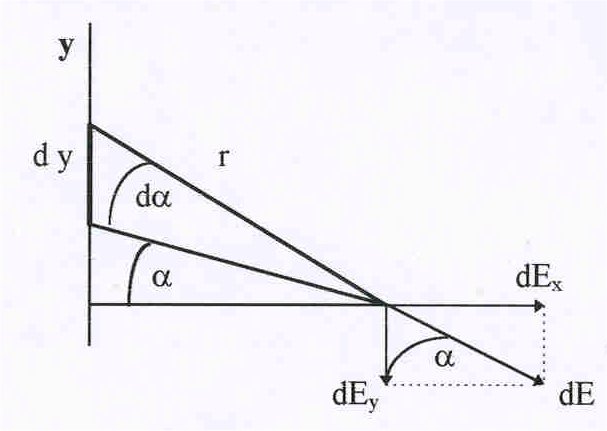
Рис.1. Вычисление поля от бесконечной нити.
ростой пример: найти напряженность электрического поля, которую создает бесконечная нить, равномерно заряженная по длине с линейной плотностью τ. Для решения этой задачи необходимо найти поле от бесконечно малого (точечного) заряда dq и затем произвести суммирование по всей длине нити. Поле от заряда dq на расстоянии r от него (см.рис.1) равноdE =
(1/4)(dq/r2),

dEx = dEcosα ; dEy = dEsinα ;
Ex = dEx , Ey = dEy.
Для суммирования (интегрирования в нашем случае) удобно ввести одну переменную, а остальные связать с ней при помощи геометрических соотношений. За такую переменную можно взять угол . Тогда r = x/cos, y/x0 = tg.
Из последнего соотношения следует (dy/x0) = d/cos2.
Ex
=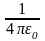
 =
=

Ey
= .
Ответ : Е =
.
Ответ : Е =
 .
.
Из приведенного примера следует, что принцип суперпозиции позволяет вычислить напряженность поля от любой конфигурации зарядов, представив ее как некую сумму бесконечно малых (точечных) зарядов. Дело лишь в том, как проводить суммирование (интегрирование). Для рассмотренного одномерного случая это простой интеграл. Для распределения зарядов по поверхности это будет двумерный (поверхностный) интеграл, для объемного распределения – трехмерный (объемный) интеграл. Для наглядного представления электрическое поле принято изображать в виде линий, названных силовыми. Под силовыми линиями понимаются линии, касательные к которым в данной точке совпадают с направлением вектора напряженности в этой точке. Кроме того, было условлено, что густота силовых линий должна быть пропорциональна величине напряженности. Силовые линии начинаются на положительных и кончаются на отрицательных зарядах. Картина силовых линий от двух точечных зарядов изображена на рис.2. Как видно из рисунка, в промежутке между зарядами силовые линии являются непрерывными.
Рис 2. Линии напряженности.
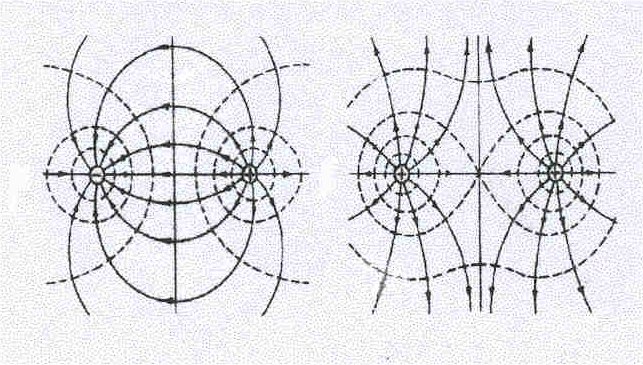
Рис. 2. Линии напряженности
Это означает, что направление векторов напряженности во всех точках однозначно, т.к. линии нигде не пересекаются. Для количественного описания силовых линий вводится понятие потока. Потоком вектора напряженности через заданную поверхность называется скалярное произведение вектора напряженности на величину этой поверхности: Ф = (ЕS). При этом предполагается, что поверхность – это вектор, причем направление этого вектора определяется направлением внешней нормали n к поверхности, т.е. нормали, проведенной в сторону выпуклости поверхности (см. рис.3): dФ = (E dS) = EdS cos = En dS. Для плоской поверхности направление внешней нормали должно задаваться дополнительными условиями.§ 1 – 4. Теорема Гаусса
|
|
Доказательство этого утверждения проводится в три этапа. Сначала теорема доказывается для точечного заряда и выпуклой поверхности. Затем рассматривается поверхность любой формы, наконец, доказательство формулируется для системы зарядов. Рассмотрим точечный заряд Q. Опишем вокруг его воображаемую сферу и вычислим полный поток через эту поверхность. Для вычисления используем определение телесного угла d (см. рис.4):
Рис.4.Телесный угол. |
|
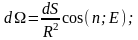
 ;
;
Ф =
 = 4 E
R2,
= 4 E
R2,
т.к. в подынтегральном
выражении величины E и R,
а полный телесный угол равен 4.
Подставляя вместо Е определение
напряженности поля для точечного заряда
Q, находим, что Ф = .
.
Рис.5. Различные формы поверхностей |
|
2. Если поверхность интегрирования имеет произвольную форму, то для заряда внутри поверхности линии напряженности пересекают ее нечетное количество раз (один или три) (см. рис.5), причем косинус угла между вектором напряженности и внешней нормалью к поверхности будет два раза положительным и один раз отрицательным (угол - тупой), так что два слагаемых общего потока компенсируют друг друга.
Если же заряд находится вне поверхности, то поток пересекает ее четное количество раз (два, четыре и т.д) так, что положительные и отрицательные (для тупых углов между n и Е) слагаемые уничтожают друг друга и общий поток оказывается равным нулю.
3. Если зарядов
несколько, то в силу принципа суперпозиции
 ;
Ф =
Фi . Для каждого
заряда в отдельности теорема доказана,
значит она остается справедливой и для
макроскопического (конечного) заряда,
который можно представить в виде суммы
точечных зарядов.
;
Ф =
Фi . Для каждого
заряда в отдельности теорема доказана,
значит она остается справедливой и для
макроскопического (конечного) заряда,
который можно представить в виде суммы
точечных зарядов.
Математическая форма записи теоремы Гаусса имеет следующий вид:
Ф0 =
 или в развернутом виде
или в развернутом виде
 .
.
Следствие: если заряды, создающие поле, находятся вне воображаемой замкнутой поверхности, то поток напряженности через эту поверхность равен нулю.
Теорема Гаусса имеет достаточно важное значение, т.к. является одним из уравнений Максвелла, которые лежат в основе теории электромагнетизма. Кроме того, эта теорема может быть использована для вычисления напряженности. Для этого необходимо, чтобы величину Е можно было вынести из-под интеграла. Это можно сделать, если Е =const на всей поверхности интегрирования. Нетрудно догадаться, что воображаемая замкнутая поверхность должна иметь симметрию, подобную симметрии расположения зарядов. При этом удобно ее выбрать так, чтобы косинус угла между вектором Е и нормалью к поверхности принимал значения либо 1 либо 0. Таким условиям удовлетворяют три класса симметрии: сферическая, цилиндрическая и зеркальная, однако в двух последних случаях необходимо пренебрегать краевыми эффектами, т.к. на краях нарушается распределение силовых линий. Ясно, что для выбора конфигурации поверхности необходимо знать, как направлен вектор Е. Здесь важно учитывать, что для статических зарядов напряженность поля вблизи зарядов должна быть перпендикулярной поверхности области распределения зарядов. В противном случае всегда будет составляющая поля, направленная вдоль поверхности распределения, что может вызвать электрический ток, и статическое распределение будет нарушено. Для иллюстрации полезно рассмотреть два примера.
Поле от бесконечной плоскости.
Рис.6. Поле от плоскости. |
|
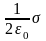 .
.
Поле от заряженной сферы.
Рис.7. Поле от сферы. |
|

§ 1 – 5. Работа по перемещению заряда в электрическом поле
Как уже отмечалось,
на электрический заряд q
со стороны поля, созданного зарядом Q,
действует кулоновская сила. Поэтому
при перемещении заряда q
в поле совершается работа, величина
которой определяется выражением dA
= Fldlcos,
где - угол между
направлениями силы и перемещения (см.
рис 8).Учитывая, что Fcos
= Fl
имеем dA = Fldl.
Для нашего случая F = qE;
qE =
 Из
рис. видно, что dlcos
=dR, и малая работа в поле
равна
Из
рис. видно, что dlcos
=dR, и малая работа в поле
равна
dA =
 ;
A =
;
A =
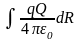 =
=
 .
.
|
|
 =
=
 .
.
Из независимости
работы от формы пути перемещения следует,
что работа электростатических сил по
замкнутому пути равна нулю. В этом случае
в первом интеграле величину заряда q,
вынесенную за знак интегрирования,
можно сократить. Тогда .
.
В этой формуле интеграл с кружком обозначает так называемую циркуляцию, т.е. он обозначает, что интегрирование проводится по замкнутому контуру. Справедливость этого утверждения следует из непосредственного выражения для элементарной работы при продвижении вдоль элементарного перемещения dl: dA = Edlcos =El dl, где - угол между направлением силы и перемещения.
Электростатика. Тема 2.
§ 2 – 1. Потенциал электрического поля
Как уже отмечалось, пробный заряд в электрическом поле обладает потенциальной энергией. Однако величина этой энергии зависит от величины заряда q. Для того, чтобы можно было охарактеризовать само поле, условились относить величину потенциальной энергии заряда q к величине этого заряда. Эту величину принято называть потенциалом электрического поля. Здесь необходимо напомнить, что само определение потенциальной энергии содержит в себе неоднозначность, т.к. эта энергия определена с точностью до некоторой постоянной. Для однозначной характеристики электрического поля принято определять эту постоянную при удалении заряда q на бесконечность. Считается, что два заряда, удаленные друг от друга на бесконечность, не взаимодействуют, т.е. их энергия взаимодействия и, следовательно, постоянная равны нулю. Поэтому можно сказать, что потенциалом электрического поля называется работа по перемещению единичного положительного заряда из данной точки поля в бесконечность. Из выражения для работы А следует, что потенциал равен
=

Потенциал – величина скалярная, он удовлетворяет принципу суперпозиции, т.е. потенциал от суммы зарядов равен сумме потенциалов от каждого заряда в отдельности. Если заряд q равный 1 Кулону, перемещается из одной точки поля в другую, то соответствующую работу называют разностью потенциалов или напряжением U, т.е.
=U
=
 ;
;
где R1 и R2 соответствуют начальному и конечному положению единичного положительного заряда. Единицей напряжения, как известно, служит один Вольт. При перемещении произвольного заряда q величина совершаемой работы увеличивается в q раз.
Связь между потенциалом и напряженностью электрического поля.
Связь между потенциалом и напряженностью поля легко установить из выражения для элементарной работы dA. Так dA можно записать через напряженность поля Е и перемещение dl: dA = qEcosdl, где - угол между Е и dl. С другой стороны, используя определение потенциала, работа dA = qd . Из этих выражений следует, что d = Ecosdl = El dl, и
=
 .
.
Обратная связь между
напряженностью и приращением потенциала
должна иметь вид
 ,
однако следует отметить, что напряженность
поля – вектор. Поэтому производная
,
однако следует отметить, что напряженность
поля – вектор. Поэтому производная
 должна иметь смысл производной по
направлению. Для положительного
заряда вектора напряженности положительны
и направлены от заряда и в сторону
уменьшения потенциала. Поэтому перед
производной необходимо поставить знак
минус, т.е.
должна иметь смысл производной по
направлению. Для положительного
заряда вектора напряженности положительны
и направлены от заряда и в сторону
уменьшения потенциала. Поэтому перед
производной необходимо поставить знак
минус, т.е.
 .
.
Из этого выражения видно, что величина производной зависит от угла между Е и dl. Так для направления, перпендикулярного Е , проекция El равна нулю; наоборот, для направления вдоль Е производная по dl максимальна и равна Е.
Термин «производная по направлению» становится более понятным в применении к прямоугольным координатам. Рассматривая поочередно проекции Е на оси x,y и z можно написать:



где


 - единичные вектора вдоль осей x,
y и z
соответственно. Сам вектор Е находится
как сумма:
- единичные вектора вдоль осей x,
y и z
соответственно. Сам вектор Е находится
как сумма:
 .
.
В теории поля производная по направлению наибольшего изменения функции называется градиентом (grad ), т.е. связь между напряженностью и потенциалом имеет вид:
E = - grad .
В направлении, перпендикулярном вектору Е, величина производной от потенциала равна нулю, т.е. в этом направлении потенциал остается постоянным. Линии или поверхности, соединяющие точки с одинаковыми потенциалами, принято называть эквипотенциальными. Примером топологии эквипотенциалей может служить рис.2 предыдущей лекции. Соотношение Е = - l показывает, что напряженность поля можно измерять в единицах Вольт / метр.
§ 2 – 2 Проводники в электрическом поле
Статический заряд на проводниках распределяется так, чтобы поле внутри проводника было бы равно нулю. В противном случае возникновение электрического поля приведет к движению зарядов. Напомним, что проводники (металлы) характеризуются наличием свободных электронов. Нас же интересует статический случай, когда движение зарядов уже прекратилось. Поэтому заряды могут располагаться только на поверхности проводника, причем так, чтобы эта поверхность была эквипотенциальной, иначе при наличии разности в проводнике опять возникнет электрический ток. Напряженность поля вблизи поверхности можно найти по теореме Гаусса, выбирая на ней достаточно малый элемент площади так, чтобы поле сохраняло свою однородность. Можно выбрать этот элемент так же, как и при вычислении поля от заряженной плоскости (см. рис.6) с той лишь разницей, что поток через основание параллелепипеда, лежащее внутри проводника, будет равен нулю ( поля внутри проводника нет). С учетом этого
 .
.
Рис.9. Поле на остриях. |
|
На незаряженном проводнике, помещенном в электрическое поле, происходит индукция зарядов. При этом заряды на ближнем и дальнем концах проводника по отношению к источнику поля имеют разные знаки так, что при исчезновении поля суммарный заряд на проводнике снова оказывается равным нулю. Это явление известно как электростатическая индукция. Однако внешнее поле не может проникнуть внутрь проводника, что используется для так называемой электростатической экранировки: экранируемый объект обшивается металлическими листами. Обратное, вообще говоря, неверно: если внутри металлической полости по каким-либо причинам возникли заряды, то их действие распространяется за металлический экран. Чтобы этого не происходило, экран требуется заземлить.
§ 2 – 3. Электроемкость
Между зарядом и потенциалом проводника существует определенная взаимосвязь. Коэффициент пропорциональности между ними носит название электроемкости или просто емкости: С =q. Взяв приращение от обеих частей, имеем: С =q или CU =q. Отсюда
 .
Единицей емкости является фарад (1F)
. 1F =
.
Единицей емкости является фарад (1F)
. 1F = ;
10-6 фарад = 1 мкф (микрофарад), 10-12
фарад = 1 пкф (пикофарад). Величину
емкости любого проводника легко
определить, деля величину заряда
проводника на его потенциал. Так
металлический шар радиуса R,
несущий заряд Q, имеет
потенциал
;
10-6 фарад = 1 мкф (микрофарад), 10-12
фарад = 1 пкф (пикофарад). Величину
емкости любого проводника легко
определить, деля величину заряда
проводника на его потенциал. Так
металлический шар радиуса R,
несущий заряд Q, имеет
потенциал

Следовательно, его емкость С равна С = 40R.
Рис.10. К расчету емкости плоского конденсатора. |
|
поля от бесконечной заряженной пластины определяется формулой
 ,
,
где Q/S – заряд на единицу площади. Если пластины расположены достаточно близко друг к другу, так что поле сосредоточено в области между ними, то, как это видно из рис.10, поля от каждой пластины складываются в области между пластинами и уничтожаются в области снаружи пластин. В этом случае в области между пластинами напряженность поля равна E = /0 и не зависит от расстояния (поле является однородным). Напряжение между пластинами U = Ed, где d – расстояние между пластинами. Поэтому емкость плоского конденсатора Сплс равна
Сплс =

Забегая немного
вперед, можно обобщить это выражения
для случая, когда область между пластинами
заполнена диэлектриком с диэлектрической
проницаемостью ,
 .
.
Известны и другие формы конденсаторов. Так, например, цилиндрические обкладки, разделенные слоем стекла, образуют так называемую лейденскую банку. В экспериментах по наблюдению фотоэффекта часто используется шаровой конденсатор. Не так давно, когда в радиотехнике использовались отдельные детали, был популярен трубчатый конденсатор.
Соединение конденсаторов.
Рис.11.Соединение конденсаторов. |
|
 ;
;
для последовательного соединения заряды на всех конденсаторах одинаковы, а складываются в этом случае напряжения:
 ;
;
 ;
;
 .
.
В частности, для двух последовательно соединенных конденсаторов общая емкость определяется как:

Энергия заряженного конденсатора.
Пусть имеется конденсатор емкости С, заряженный до напряжения U. Для того, чтобы перенести на него добавочный заряд dQ требуется совершить работу dA = UdQ; но в конденсаторе заряд и напряжение связаны соотношением Q = CU, дифференцируя которое, получим dQ =CdU. Тогда dA =CUdU, и полная работа, которую надо совершить для заряда конденсатора
 .
.
Эта работа превращается
в энергию электрического поля конденсатора
 .
Если учесть, что объем конденсатора V
= Sd, то можно говорить о
плотности энергии w, где
.
Если учесть, что объем конденсатора V
= Sd, то можно говорить о
плотности энергии w, где
w = .
Подставляя в последнюю формулу выражение
для емкости плоского конденсатора и
учитывая, что U = Ed
= d/0
, находим:
.
Подставляя в последнюю формулу выражение
для емкости плоского конденсатора и
учитывая, что U = Ed
= d/0
, находим:
 w =
w =
 .
.
Последнее выражение характеризует плотность энергии электрического поля.
Диэлектрики. Тема 3.
§ 3-1. Электрический диполь
Рис.12. Поле диполя. |
|
дипольный момент р = ql, где l – вектор, проведенный из центра отрицательного заряда к центру положительного. Хотя в целом диполь нейтрален, тем не менее несовпадение центров положительного и отрицательного зарядов приводит к тому, что вокруг диполя образуется электрическое поле. Его можно вычислить по принципу суперпозиции. Наиболее просты расчеты для двух случаев: вычисления поля вдоль оси диполя и для точки, находящейся на перпендикуляре, восстановленным из середины l. Пусть точка А, где требуется найти поле диполя, отстоит от положительного заряда на расстояние х. Тогда напряженность поля от этого заряда в точке А равна:
 а
от отрицательного заряда
а
от отрицательного заряда

Общее поле Е0 двух зарядов равно (см. рис.12)

 -
-
 =
=
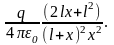
Для расстояний х l выражение для Е0 упрощается: (l+x) x и
 .
.
Для вычисления
напряженности в точке В достаточно
вспомнить, что меньшая диагональ Е
ромба (см рис12) со стороной Е+ равна
Е =2Е+сos
.Кроме того, из рис.12 следует, что
 ;
и
;
и

 .
.
Поскольку величина Е непрерывна, то при переходе от точки А к точке В значение Е должно меняться постепенно, и для произвольной точки можно показать, что
Е0 =
 ,
,
где N
– некий поправочный коэффициент,
меняющийся от 1 до 2 при изменении
положения точки. Точный расчет показывает,
что N =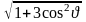 ,
где
,
где
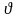 - угол между направлением радиуса-
вектора точки и осью диполя. В рамках
нашего курса этот расчет проводиться
не будет.
- угол между направлением радиуса-
вектора точки и осью диполя. В рамках
нашего курса этот расчет проводиться
не будет.
§
Рис.13. Ориентирующее действие на диполь внешнего поля. |
|
 ;
для большинства диэлектриков эта
величина оказывается незначительной,
и ее можно считать пропорциональной
напряженности внешнего поля Р = 0
Е. Величина (каппа)
называется диэлектрической
восприимчивостью. Разбиение коэффициента
пропорциональности на два сомножителя
и 0
связано с требованиями размерности в
системе СИ.
;
для большинства диэлектриков эта
величина оказывается незначительной,
и ее можно считать пропорциональной
напряженности внешнего поля Р = 0
Е. Величина (каппа)
называется диэлектрической
восприимчивостью. Разбиение коэффициента
пропорциональности на два сомножителя
и 0
связано с требованиями размерности в
системе СИ.
§ 3-3 Теорема о поляризационных зарядах
Рис.14. Вычисление поляризационного заряда. |
|
При поляризации происходит смещение положительных зарядов в направлении напряженности и отрицательных – в противоположном. Как видно из рис.14, через те участки поверхности, где напряженность направлена внутрь поверхности, часть отрицательных зарядов покинет рассматриваемую область, а через участки, где напряженность направлена наружу, в область войдет отрицательный заряд. Если вошедший и вышедший заряды не равны друг другу, то область приобретет поляризационный заряд Qп. Для участка поверхности S (правая часть рис.14) через S войдут отрицательные заряды тех и только тех молекул, которые находятся в параллелепипеде с площадью основания S и высотой lcos, где l – величина возможного смещения зарядов в молекуле, а - угол между внешней нормалью к поверхности и вектором поляризации. Объем параллелепипеда равен S lcos, следовательно в нем находится n0S lcos молекул (n0 –концентрация молекул). При этом левому основанию параллелепипеда должна соответствовать внешняя нормаль, направленная налево (угол - тупой), а для правого основания - угол - острый. Через левое основание выходит, а через правое – входит отрицательный заряд. Поэтому и для левого и для правого оснований появится знак минус, т.е. Qп = - q n0S lcos ( q- заряд каждой молекулы). Учитывая, что q n0 l = Р0 – величина вектора поляризации и Р0 cos=Рn , получим: Qп = - Рn S.
Интегрируя это выражение по всей замкнутой поверхности S, имеем:
 .
.
Полученная формула, вообще говоря, справедлива для неоднородного диэлектрика. Для однородного же поляризационные заряды могут возникать только на поверхности, причем поверхностная плотность зарядов = Qп /S = Pn . Действительно, подставляя в последнее выражение значение Pn =0 En , нетрудно получить, что
= -

 dS
dS
 ;
но по теореме Гаусса
;
но по теореме Гаусса
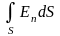 =
=
 и
=
-
и
=
- ;
при
0 , это может выполняться лишь при
=
0.
;
при
0 , это может выполняться лишь при
=
0.
§ 3-4. Вектор электрического смещения
Из изложенного ясно, что в диэлектриках кроме внешнего поля существует еще и собственное (внутреннее) поле, поэтому можно ожидать, что Еполн = Есвоб + Епол . Однако, принцип суперпозиции в общем случае здесь не пригоден, т.к. он справедлив лишь для определенно заданного распределения зарядов, в то время как распределение зарядов в диэлектрике само определяется искомым электрическим полем. Поэтому каждое из слагаемых должно быть определено из каких-то других соображений.
Рассмотрим замкнутую поверхность, внутри которой есть свободные Qс и поляризационные Qп заряды. Тогда теорема Гаусса принимает следующий вид:
 .
.
Заменяя величину Qп согласно теореме о поляризационных зарядах, можно найти:
 .
.
Помножим обе части последнего уравнения на 0 и перенесем интеграл из правой части в левую. Получаем, что
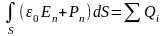 .
.
Выражение, стоящее
в круглых скобках под знаком интеграла,
представляет собой новый вектор ,
называемый вектором электрического
смещения или вектором электрической
индукции. Его можно представить так:
,
называемый вектором электрического
смещения или вектором электрической
индукции. Его можно представить так:
 ,
,
где (1+)
= называют
относительной диэлектрической
проницаемостью вещества. Тогда
 .
.
Для вектора
электрического смещения теорема Гаусса
такова .
.
Постоянный ток. Тема 4.
§ 4-1. Основные определения
Известно, что электрический ток – это направленное движение электрических зарядов. Если количество зарядов, проходящее через заданную площадь в единицу времени не меняется с течением времени, то такой ток называют постоянным. Ясно, что движение может быть направленным только под влиянием внешних электрических сил. Для того, чтобы ток оставался постоянным с течением времени, электрическая цепь, т.е. ряд проводников, соединенных параллельно и последовательно друг другу, должна быть замкнутой.
Отсюда следует, что силы не могут быть электростатическими, т.к. работа этих сил по замкнутому контуру всегда равна нулю. Обычно эти силы называют сторонними, подчеркивая их неэлектростатическое происхождение. Сила, отнесенная к величине перемещаемого заряда, по аналогии с электростатикой, называется напряженностью, а работа по перемещению единичного положительного заряда на каком-либо участке получила название электродвижущей силы. Однако обычно принято говорить об электродвижущей силе источника тока E, понимая под этим работу, совершаемую источником во всей цепи. Поскольку ЭДС – это работа, то между нею и напряженностью сторонних сил остается справедливым соотношение, полученное в электростатике 4:
E = .
При разомкнутой цепи сторонние силы источника так перераспределяют заряды, что создаваемое ими поле компенсирует действие сторонних сил внутри источника. При замкнутой цепи заряды распределяются и вдоль проводников внешней цепи, создавая поле внутри их.
Если на каком- либо участке цепи действуют сторонние и электростатические силы, то работа по перемещению единичного положительного заряда будет складываться из работ каждой из этих сил по отдельности. Величину общей работы принято называть напряжением. Если понятие “участок” распространить на всю цепь, то очевидно, что тогда общая работа равна E.
§ 4-2. Закон Ома
Для выяснения закономерностей постоянного тока обратимся к упрощенной микроскопической картине. Рассмотрим отдельный заряд величиной q 0 , являющийся одним из носителей тока в проводнике ( для металлов q0 = -е, где е – заряд электрона). В силу теплового движения каждый заряд движется хаотически, а под действием сторонних сил он приобретает еще и направленное движение. При хаотическом движении заряд постоянно сталкивается с ионами, масса и размеры которых значительно больше аналогичных параметров носителя. Ионы также участвуют в тепловом движении, но это, в основном, колебательные движения, амплитуда которых увеличивается с температурой. Носители, сталкиваясь с ионами, на какое – то мгновение как бы прилипают к последним (разноименные заряды стремятся притянуться друг к другу). На языке механики это означает, что носители испытывают неупругие столкновение с ионами так, что новый путь они начинают с нулевой скоростью направленного движения. Пусть время между двумя последовательными соударениями равно . Тогда под действием напряженности носитель за это время приобретет скорость u =a. Ускорение а =F/m = q0 E/m; m – масса носителя. Вводя понятие плотности тока j , которое определяется как количество зарядов, проходящих через единичную площадку, перпендикулярную вектору скорости, можно записать:
 где
где

 .
.
Величина , определенная таким способом, называется электропроводностью материала, а обратная ей =1/ -удельным сопротивлением. Нетрудно заметить, что плотность тока – вектор, направление которого совпадает с направлением вектора скорости. Соотношение j =E носит название закона Ома в дифференциальной (векторной) форме.
Если однородный проводник имеет длину l и площадь поперечного сечения S, то закон Ома для такого проводника может быть записан в несколько ином виде. Для этого умножим обе части соотношения j =E на произведение lS и учтем, что для однородного проводника поле внутри его везде одинаково, т.е. однородно, и El =U – разность потенциалов на концах проводника. Тогда получим:
jSl =El S.
Введем понятие силы тока I = (jS) и обозначим l/ S =R, теперь наше соотношение приобретает обычный вид: U =IR, где U – напряжение на концах проводника, а I –сила тока.
Сила тока – скалярное произведение плотности тока и площади, которой в этом случае приписываются векторные свойства ( направление вектора определяется как и прежде направлением внешней нормали к площади). Величина R называется сопротивлением проводника.
Для соединения нескольких проводников величина общего сопротивления R0 находится по известным правилам: для последовательного соединения R0 = Ri , а для параллельного
 .
.
Если на рассматриваемом участке имеется источник тока с ЭДС E , как уже отмечалось, общее напряжение складывается из разности потенциалов и ЭДС, т.е.
U =IR +E .
Этот вариант записи соотношения между током и напряжением носит название закона Ома для участка цепи, содержащей ЭДС. Здесь важно учитывать правило знаков: считается, что положительный ток проходит от положительного полюса элемента к отрицательному; при заданном направлении тока через рассматриваемый участок, ЭДС считается положительной, если она создает ток в этом же направлении и отрицательной – если в противоположном. Для замкнутой цепи очевидно, что концы проводника замыкаются сами на себя и U=0. Тогда закон Ома примет вид
E = (R + r)I,
где r – внутреннее сопротивление источника тока.
§ 4-3. Закон Джоуля – Ленца
При выводе дифференциального закона Ома предполагалось, что носители тока в момент столкновения с ионами как бы прилипают на мгновение к последним, т.е. носители полностью теряют свою энергию, которую они приобрели под действием ускоряющего поля. Эта энергия передается ионам и переходит в энергию их хаотических колебаний, т.е. в теплоту.
За время свободного пробега отдельный носитель приобретает энергию, равную работе, которая совершается за счет электрического поля: w = q0El l. Т.к. общее количество зарядов, проходящее в единицу времени через поверхность единичной площади, определятся плотностью тока j , то для l = 1 количество энергии, переходящей в теплоту, равно W =jE или
W = Е2.
Последнее выражение носит наименование дифференциального закона Джоуля-Ленца.
Для проводника, имеющего длину l и площадь S, оно преобразуется к известному виду, достаточно лишь обе части этого выражения умножить на объем V =Sl .
WV
=W0 = ,
,
где в преобразованиях использован закон Ома для участка цепи. Полученная формула описывает закон Джоуля-Ленца в интегральном виде.
Выделяющаяся теплота имеет смысл полезной лишь в нагревательных приборах; во всех других случаях это – потери энергии, снижение этих потерь составляет одну из важнейших задач электротехники. Эта теплота образуется зя счет энергии сторонних сил.
Для замкнутой цепи полная работа по перемещению единичного положительного заряда по определению равна E, значит полная мощность, которую может развить источник, равна E I. Величина совершенной работы за время t определится как A =E It.
§ 4-4. Основы зонной теории
До сих пор развитие наших представлений об электричестве происходило достаточно последовательно с использованием довольно простых моделей. Лишь в какой-то момент было стыдливо использовано понятие носителей с зарядом q0 , хотя тут же оговаривалось, что в действительности надо рассматривать электроны, которые ответственны за проводимость металлов. Однако электроны являются довольно своеобразным микроскопическими объектами, которые плохо подчиняются законам классической механики. Более того, их свойства часто описываются лишь в представлениях квантовой теории и теории вероятности.
Наиболее известным следствием квантовомеханической теории является описание свойств электронов с помощью квантовых чисел: n, l, m и s, где
n – главное квантовое число, характеризующее энергию электрона,
l, - орбитальное квантовое число, определяющее форму орбиты,
m – магнитное квантовое число, связанное с ориентацией орбиты,
s – спиновое число, определяющее собственный момент импульса электрона.
Первые три квантовых числа могут принимать только целочисленные значения –1, 2…и т.д, а s – только два значения - ½, и одному набору чисел n, l и m соответствуют два электрона с противоположно направленными спинами.
Достаточно известным является и так называемый принцип Паули: в атомах не бывает двух электронов с одинаковыми квантовыми числами.
Из этих двух положений следует, что энергия электронов может принимать только определенные дискретные значения так, что по мере увеличения числа электронов в атоме внешние электроны даже при температуре 0 К обладают конечной энергией.
Рис.15. Схема расположения зон. |
|
Указанный тип проводимости в полупроводниках называется собственной проводимостью. Он наблюдается только в очень чистых материалах. Обычно же любой полупроводник содержит небольшое (примерно один атом на миллион) количество примесных атомов. Поскольку атомов примеси мало, то они не взаимодействуют между собой, и их энергетические уровни остаются нерасщепленными. Примесные энергетические уровни могут быть как пустыми, так и заполненными. Если такой заполненный примесный уровень располагается в запрещенной зоне чуть ниже зоны проводимости, то под действием тепловых возбуждений электроны с этого уровня могут переходить в зону проводимости. Если же пустой уровень находится чуть выше валентной зоны, то электроны из этой зоны могут быть переброшены на вакантный примесный уровень так, что в валентной зоне образуется «дырка», способная перемещаться от одного атома к другому, создавая «дырочную» проводимость. Возникающая в обоих случаях проводимость называется примесной. При этом электронная примесная проводимость получила название донорной или n – проводимости, а «дырочная» проводимость была названа акцепторной или р – проводимостью. В настоящее время во всех полупроводниках предпочитают использовать примесную проводимость.
Комбинация полупроводников с различным типом проводимости позволили создать целый ряд кристаллических диодов и триодов, нашедших широкое применение в радиоэлектронной промышленности. Современные технологии позволяют получать на кристалле кремния размером в булавочную головку несколько десятков миллионов полупроводниковых элементов. Основным элементом любого электронного устройства стала микросхема. Преимущества их использования очевидны: они экономичны в отношении потребления энергии, малогабаритны, не боятся перегрузок и т.п. Из недостатков надо выделить два: если в микросхеме выходит из строя всего один элемент, то починить ее невозможно. Ремонт сводится к замене неисправной микросхемы, что стоит довольно дорого. Наконец, все микросхемы оказываются крайне чувствительны к воздействию проникающего излучения. В условиях повышенной радиационной опасности их приходится заменять радиосхемами на сверхминиатюрных лампах.
§ 4-5. Зависимость проводимости материалов от температуры
Из рассмотрения проводимости металлов следует, что их сопротивление обусловлено взаимодействием носителей с колеблющимися ионами. Поскольку с повышением температуры амплитуда тепловых колебаний увеличивается, и носители начинают чаще сталкиваться с ними, можно сделать заключение о том, что с повышением температуры сопротивление проводников должно увеличиваться. Для полупроводников же картина обратная – чем выше температура, тем больше носителей, т.е. сопротивление полупроводников падает с повышением температуры.
С понижением температуры сопротивление проводников должно уменьшаться, достигая минимума при абсолютном нуле. Однако в действительности при низких, но конечных температурах сопротивление некоторых металлов скачком падает до нуля. Это явление было открыто в 1911 г и получило название сверхпроводимости. Долгое время для его наблюдения требовались температуры, близкие к температуре жидкого гелия, и лишь сравнительно недавно удалось повысить температуру сверхпроводящего перехода до значения 90-100 К. Сверхпроводимость стало возможным наблюдать при температуре жидкого азота. Природа возникновения сверхпроводимости может быть объяснена только в рамках квантовой теории.
§ 4-6. Правила Кирхгофа
Рис.16. К правилам Кирхгофа. |
. |
I1 – I2 + I3 –I4 = 0,
2. I1 R1 + I2 R2 - I4 R4 + I3 R3 = E3 – E2 – E1
Постоянное магнитное поле. Тема 5.
§ 5 –1. Закон Ампера
Рис.17. Взаимодействие двух элементов тока. |
|
 ,
,
 ,
,
где смысл принятых обозначений ясен из рис.17 и 18. Величина k как и прежде введена из соображений размерности. В системе СИ она равна 0 4; значение постоянной 0 , которую принято называть магнитной постоянной вакуума, записывается так:
0 = 4
10 –7
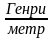 .
.
Для определения силы как вектора закон Ампера должен быть изменен так, чтобы справа стояло векторное произведение:
 ,
,
 .
.
По аналогии с электростатическим полем для характеристики магнитного поля можно ввести силовую величину, отнесенную к единичному элементу тока. В теории магнетизма эту величину принято называть магнитной индукцией, точнее вектором магнитной индукции. Тогда закон Ампера для произвольного элемента тока I2 dl2 может быть записан как
dF2
= I2
[dl2
dB], dB =
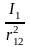 dl1sin1
, dB = k
[dl1,r12]
.
dl1sin1
, dB = k
[dl1,r12]
.
Это определение как модуля, так и самого вектора dB носит название закона Био-Савара-Лапласа.
Рис.18. Правило правого винта. |
|
 .
.
Сила максимальна,
когда dl
перпендикулярно направлению В. В этом
случае В определяется как:
 .
.
Отсюда единица измерения магнитной индукции в системе СИ, называемая тесла, определяется как 1Н/ (1A1M).
Магнитное поле можно наглядно изобразить с помощью силовых линий, проводя их по тем же правилам, что и в электростатике, но характер этих линий – другой. Как уже отмечалось, магнитных зарядов не существует, поэтому свойства силовых линий магнитного поля отличаются от свойств электростатического поля. Из следствия теоремы Гаусса вытекает, что поток вектора В через любую замкнутую поверхность должен равняться нулю, т.е. силовые линии магнитной индукции непрерывны, и
 .
.
Теоретический расчет
величины В для конкретной конфигурации
проводников производится на основании
закона Био-Савара-Лапласа с использованием
принципа суперпозиции
 ,
где суммирование производится по всем
проводникам, образующих данную систему.
,
где суммирование производится по всем
проводникам, образующих данную систему.
§ 5 –2. Поле прямого тока и витка с током
В качестве примеров расчета значений вектора магнитной индукции вычислим поле прямого тока и в центре круглого витка с током.
Поле прямого тока.
Рис.19. Поле прямого тока. |
|

Для суммирования
свяжем все переменные друг с другом,
выбирая в качестве интегрируемой
переменной угол .
Из рис.19 видно, что

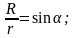
 ;
;
 .
.
Подставляя эти
выражения в формулу для В, после
преобразований получим:
 ;
;

где 1
и 2 – углы,
соответствующие направлениям на концы
проводника. Если проводник бесконечный,
то 1
0, а 2
, и
 .
.
Направление вектора В определяется правилом вычисления векторного произведения: первый сомножитель (dl в нашем случае) вращается в направлении наименьшего угла ко второму сомножителю (r). Направление движения оси правого винта при таком вращении покажет направление их векторного произведения ( на рис.- от нас – значок -). Силовые линии магнитного поля являются концентрическими окружностями, охватывающими проводник с током. Все они лежат в плоскости, перпендикулярной направлению тока.
Поле витка с током.
Рис.20. Поле в центре витка с током. |
|
 .
.
В се
элементы тока дают одинаковое направление
вектора dB так ,что суммарный
вектор В перпендикулярен плоскости
чертежа и направлен на нас (значок
).
се
элементы тока дают одинаковое направление
вектора dB так ,что суммарный
вектор В перпендикулярен плоскости
чертежа и направлен на нас (значок
).
§ 5 –3. Теорема о циркуляции магнитного поля
Рис.21. Вычисление циркуляции. |
|
Если суммирование
проводится по всей длине окружности,
то результат носит название циркуляции,
т.е. его можно записать так
 .Для
выбранного нами контура в виде окружности
величина интеграла может быть вычислена
непосредственно. Во всех точках контура
вектора В направлены по касательной к
окружности, а значения В постоянны и
равны В =
.Для
выбранного нами контура в виде окружности
величина интеграла может быть вычислена
непосредственно. Во всех точках контура
вектора В направлены по касательной к
окружности, а значения В постоянны и
равны В = ,
так что его можно вынести за знак
интеграла. Тогда
,
так что его можно вынести за знак
интеграла. Тогда
 =
2R и
циркуляция
=
2R и
циркуляция
 .
.
Рис.22. К расчету элемента контура. |
|
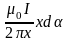 и не зависит от расстояния х от тока до
элемента контура. Угол d
означает малый угол, под которым виден
элемент длины контура из точки пересечения
его площади током. Очевидно, что полное
значение суммирования не изменится и
для произвольной формы контура, который
удобно в этом случае представить как
ломаную линию, состоящую из элементов
окружностей и приращений радиуса. Здесь
следует помнить, что проекции вектора
В на приращения радиуса равны нулю.
и не зависит от расстояния х от тока до
элемента контура. Угол d
означает малый угол, под которым виден
элемент длины контура из точки пересечения
его площади током. Очевидно, что полное
значение суммирования не изменится и
для произвольной формы контура, который
удобно в этом случае представить как
ломаную линию, состоящую из элементов
окружностей и приращений радиуса. Здесь
следует помнить, что проекции вектора
В на приращения радиуса равны нулю.
Если плоскость, в которой лежит наш мысленный контур, не перпендикулярен направлению тока, то контур можно спроектировать на плоскость, нормальную к току, снова результат вычисления циркуляции будет прежний. Если через плоскость нашего контура проходит несколько токов I1, I2 и т.д., то поскольку выражение для циркуляции остается справедливым для каждого тока в отдельности, оно останется справедливым и для суммы токов. Итак, в общем можно записать:
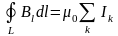 .
.
Полученное выражение носит название теоремы о циркуляции и является одним из уравнений Максвелла. Суммирование в правой части этого уравнения носит алгебраический характер: токи могут иметь знак (+) или (-) в зависимости от того, острый или тупой углы образуют они с направлением заданной нормали к площади, охватываемой контуром. Поля, циркуляция которых отлична от нуля, называются вихревыми.
Словесная формулировка теоремы о циркуляции:
Циркуляция вектора магнитной индукции по замкнутому контуру с точностью до постоянного множителя 0 равна алгебраической сумме токов, охватываемых этим контуром.
§ 5 –4. Поле длинного соленоида
Рис.23. Силовые линии магнитного поля соленоида. |
|
 +
+
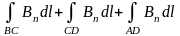 .
.
Однако на трех из
них значения Вn
равны нулю: на отрезках АВ и СD
вектор В перпендикулярен этим сторонам,
а отрезок ВС можно удалить в бесконечность,
где В = 0. На отрезке AD
значения В постоянны, и ВlC
, где l C
- длина соленоида. Т.к. ток I
пересекает контур N раз
( N- число витков) , то Вl
C = 0
NI, откуда В =0
nI, где n =N/
l C
ВlC
, где l C
- длина соленоида. Т.к. ток I
пересекает контур N раз
( N- число витков) , то Вl
C = 0
NI, откуда В =0
nI, где n =N/
l C
Силы, действующие в магнитном поле. Тема 6.
§ 6 – 1. Взаимодействие прямых проводников
Вообще говоря, силу действия на проводник с током, помещенный в магнитное пол, можно вычислить пользуясь законом Ампера, который был сформулирован на прошлой лекции. Однако для упрощения математических выкладок предположим, что величина поля определена заранее. Пусть это поле однородное, т.е. его значение одинаково во всех точках рассматриваемого пространства. Тогда сила, действующая на элемент тока, записывается в таком виде:
dF = IBdlsin, где - угол между направлением В и элементом тока Idl.
Рис.24. Взаимодействие двух прямых проводников. |
|
F = IBLsin.
Наиболее простой вид эта формула приобретает для случая взаимодействия двух прямых проводников. Для простоты будем считать их бесконечными так, что поле, создаваемое проводником, по которому проходит ток I1, во всех точках другого проводника с током I2 (см. рис.24), имеет одно и то же значение, если проводники параллельны друг другу. В этом случае сила, действующая на отрезок проводника длиной L с током I2, равна F12 =BL I2, или, подставляя в эту формулу явное выражение для В, имеем:
 ( ◊ )
( ◊ )
Направление силы взаимодействия для параллельных и антипараллельных взаимодействующих токов показано на рис.24. Из рисунка видно, что параллельные токи притягиваются, а токи с противоположным направлением отталкиваются друг от друга. Формулу ( ◊ ) используют для определения единицы измерения силы тока – ампера. Полагая I1=I2 = 1A, R = 1M и L = 1M, можно вычислить, что сила взаимодействия равна 210-7Н, т.е. за единицу силы тока принимают такой ток, который, протекая по параллельным проводам, отстоящим друг от друга на расстояние 1м, вызывает силу 210-7Н, действующую на единицу длины проводника.
§ 6 – 2. Действие магнитного поля на контур с током
Рис.25. Действие магнитного поля на рамку с током. |
|
Напомним, что момент силы М определяется векторным произведением радиуса-вектора, проведенного от оси в точку приложения силы, на саму силу.
Вычислим моменты всех сил относительно оси z, проходящей через центр рамки ( см. рис.25). Из рисунка видно, что моменты сил F2 и F4 равны нулю. Момент силы F1 M1 = F1sin b/2 = IB sin b/2 = (1/2)ISBsin, где ab = S – площадь рамки. Момент силы F3 также равен М1, так что суммарный момент сил равен:
 ,
,
где введенная величина рм =IS носит название магнитного момента рамки. Если магнитному моменту приписать векторные свойства, определяя его направление по правилу правого винта, движение оси которого определяется, в свою очередь, вращением винта в направлении обтекания рамки током, то общий момент сил, действующих на рамку, равен
 .
.
Этот момент стремится повернуть рамку к положению устойчивого равновесия, при котором магнитный момент рамки направлен вдоль направления поля.
§ 6 – 3. Сила Лоренца
Рис.26. Действие силы Лоренца на движущийся заряд. |
|
 .
.
Тогда сила, действующая на проводник с током в однородном магнитном поле В может быть записана как
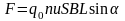 .
.
Из этого равенства можно определить силу, действующую на отдельный заряд q0 . Оценивая количество зарядов в проводнике N = nSL, нетрудно найти, что сила, известная в физике как сила Лоренца, равна FЛ =q0uBsin.
Учитывая, что скорость
направленного движения зарядов в
проводнике – –вектор,
и что направление силы определяется по
правилу правого винта, можно определить
силу Лоренца как
–вектор,
и что направление силы определяется по
правилу правого винта, можно определить
силу Лоренца как
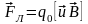 .
.
Сила Лоренца
максимальна, когда скорость отдельного
заряда перпендикулярна вектору В, и
равна нулю, когда заряд движется
параллельно силовым линиям магнитного
поля. В первом случае заряд вращается
по окружности, радиус которой определяется
законом Ньютона:
 ;
;
 .
.
В общем случае, когда скорость заряда составляет с направлением поля произвольный угол (см. рис.26.), траектория движения представляет собой винтовую линию, ось которой совпадает с направлением поля. Движение заряда можно рассматривать в этом случае как сложение двух движений: вращения вокруг направления поля, обусловленного составляющей вектора скорости, нормальной к направлению В, и поступательного движения со скоростью, равной другой составляющей, параллельной полю.
Это свойство заряженных частиц вращаться в поперечном магнитном поле используется для получения элементарных частиц с большими энергиями. Устройства, предназначенные для этого, называются циклотронами. Наиболее известны модификации этих устройств, которые называются синхрофазотронами. Усложнение конструкции ( и названия) связано с тем, что в процессе ускорения частицы приобретают скорость, близкую к скорости света, вследствие чего их масса увеличивается, и они выпадают из условия синхронизма. Поэтому приходится увеличивать поле или уменьшать частоту напряжения.
§ 6 – 4. Электромагнитная индукция
Из школьного курса физики известно, что при изменении магнитного поля, пронизывающего некую поверхность, ограниченную замкнутым проводящим контуром, в этом контуре возникает ЭДС, равная с обратным знаком скорости изменения магнитного потока. Это явление было открыто в 1831 году известным английским ученым М. Фарадеем, и установленный им закон носит его имя. Определяя величину магнитного потока Ф как
Ф =BS
cos
=
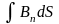 ,
,
где - угол между направлением В и нормали к площади контура, закон Фарадея можно записать в виде:
E
= - ;
;
откуда видно, что возникновение индукционного тока возможно при изменении либо величины В, либо при изменении площади контура, либо при изменении ориентации контура (вращении) относительно направления магнитного поля. Магнитный поток принято измерять в Веберах. 1 Вебер = 1Тесла м2.
Знак минус, стоящий перед производной магнитного потока отражает правило Ленца: индукционный ток направлен так, чтобы своим действием воспрепятствовать причине, его вызвавшей.
Проявлением индукционных токов являются токи Фуко, возникающие в массивных проводниках, помещенных в изменяющееся магнитное поле (например, в сердечниках трансформаторов). Для борьбы с этими токами сердечники набираются из очень тонких листов металла, разделенных прослойкой непроводящего лака.
§ 6 – 5. Самоиндукция
Важным частным случаем электромагнитной индукции является самоиндукция, т.е. возникновение ЭДС индукции в самом проводнике, порождающим изменяющееся магнитное поле. В строгой теории электромагнетизма показано, что величина магнитного потока, окружающего проводник с током, пропорциональна силе этого тока Ф = L I, где коэффициент пропорциональности L носит название коэффициента самоиндукции или индуктивности.
Качественные соображения о пропорциональности между Ф и I вытекают из закона Био-Савара-Лапласа, где установлено, что В I. Значения L определяются геометрическими свойствами проводника. Единицей измерения L в системе СИ служит Генри.
1Генри =1Вебер/Ампер.
Учитывая взаимосвязь Ф и L, можно записать
Eсам
= - .
.
Если проводник не изменяет своей формы с течением времени, то dL/dt = 0, и
Eсам
= -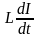 .
.
Для одного витка длинного соленоида Ф =ВS= 0 nIS, и, если полное число витков соленоида равно N= nlc, , то общий поток через весь соленоид Ф0 = Ф N = 0 n2lc IS, откуда
L = 0 n2lcS.
§ 6 – 6. Энергия магнитного поля
Пусть имеется электрическая цепь, состоящая из источника постоянного тока, сопротивления и катушки индуктивности L. Предположим, что в некоторый момент времени источник мгновенно удаляется из цепи, которая остается замкнутой. Как следствие явления самоиндукции ток в цепи не исчезнет мгновенно, т.к. его будет поддерживать возникшая ЭДС самоиндукции. В процессе убывания тока сторонние силы, ответственные за явление самоиндукции, совершат некоторую работу. За малый промежуток времени dt, когда ток и ЭДС остаются практически неизменными, сторонние силы совершат работу
dA = Eсамdq, где dq =Idt, или, используя выражение для ЭДС самоиндукции,
dA= -IdtL dI/dt, т.е. dA=-LidI.
Полную работу сил можно найти, суммируя малые работы dA за весь период исчезновения тока:
 .
.
По закону сохранения энергии эта работа может быть совершена лишь за счет энергии W, которой обладает катушка с током, поэтому
 .
.
Эту энергию можно приписать магнитному полю катушки (соленоида). Считая соленоид достаточно длинным, можно использовать формулу, связывающую индукцию поля в соленоиде с током: B =0 nI, откуда I = B/0 n. Подставляя это соотношение, а также значение L для соленоида в выражение для энергии катушки, получаем:
 .
.
Тогда плотность
магнитной энергии, т.е. энергии,
приходящейся на единицу объема V=lcS,
равна
w
= .
.
Магнитное поле в веществе. Тема 7.
§ 7 – 1. Модель молекулярных токов.
Под действием магнитного поля все тела приобретают магнитные свойства – в веществе появляются собственные магнитные поля так, что теперь поле внутри вещества складывается из внешнего поля и собственного. В этом смысле принято говорить, что все тела являются магнетиками. Простейшее объяснение проявления магнетизма связано с гипотезой молекулярных токов, высказанной еще в начале XIX века Ампером. Согласно этой гипотезе в веществе циркулируют микроскопические замкнутые токи - молекулярные токи. С точки зрения современных представлений о строении вещества нетрудно заметить, что эта гипотеза предвосхитила электронную теорию строения атома, где каждый вращающийся вокруг ядра атома электрон представляет собой элементарный круговой ток.
В отсутствие внешнего поля орбиты молекулярных токов, а, следовательно, и их магнитные моменты рМ (напомним, что рМ =IS) ориентированы хаотически в пространстве так, что вещество не проявляет никаких магнитных свойств. При наложении внешнего магнитного поля моменты ориентируются вдоль силовых линий этого поля (также как рамка с током) так, что каждый бесконечно малый объем V вещества приобретает отличный от нуля магнитный момент, - вещество намагничивается. Суммарный магнитный момент единицы объема называется намагниченностью и определяется выражением:
 .
.
В большинстве случаев значение намагниченности оказывается пропорциональным величине магнитного поля JB, где коэффициент пропорциональности носит название магнитной восприимчивости. Однако существует группа веществ, у которых упорядочение моментов происходит самопроизвольным способом. Эти вещества получили название ферромагнетиков (по названию первого известного ферромагнетика – железа).
§ 7 – 2. Связь молекулярных токов с вектором намагниченности
Рис.27. К расчету молекулярных токов. |
|
Кроме того, Jcos = Jl и IM = Jl l. Полный молекулярный ток через поверхность получим суммированием всех IM по контуру L:
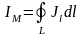 ,
т.е. полный молекулярный ток определяется
циркуляцией вектора намагниченности.
,
т.е. полный молекулярный ток определяется
циркуляцией вектора намагниченности.
Строгая теория магнетизма делает вывод, что для молекулярных токов на поверхности полученная формула сохраняет свой вид, лишь вместо IM фигурируют поверхностные тока In . В любом случае, при наличии вещества в правую часть теоремы о циркуляции добавляются молекулярные токи, и

Преобразуем это
выражение, перенося интеграл циркуляции
в левую часть. Тогда
 ()
()
Сравнивая последнее соотношение () с теоремой о циркуляции магнитного поля в вакууме, находим
 ,где обозначение В0 соответствует
магнитному полю в вакууме; нетрудно
заметить, что подынтегральные выражения
двух последних уравнений должны быть
одинаковыми. Из этого следует, что (В -
0J)
= B0 . ( ).
Как уже отмечалось, для большинства
магнетиков J
B0
. Коэффициент пропорциональности,
который требуется ввести, чтобы установить
точное соотношение между J
и B0 , зависит от
выбора системы единиц. В выбранной нами
системе СИ этот коэффициент равен 1/0
, т.е.
,где обозначение В0 соответствует
магнитному полю в вакууме; нетрудно
заметить, что подынтегральные выражения
двух последних уравнений должны быть
одинаковыми. Из этого следует, что (В -
0J)
= B0 . ( ).
Как уже отмечалось, для большинства
магнетиков J
B0
. Коэффициент пропорциональности,
который требуется ввести, чтобы установить
точное соотношение между J
и B0 , зависит от
выбора системы единиц. В выбранной нами
системе СИ этот коэффициент равен 1/0
, т.е.
 .Подставляя это выражение для
намагниченности в уравнение ( ),
получим B - B0
=B0 , и B
= (1+)B0
.Величина (1+)
=
называется относительной магнитной
проницаемостью, т.е. В =В0
.
.Подставляя это выражение для
намагниченности в уравнение ( ),
получим B - B0
=B0 , и B
= (1+)B0
.Величина (1+)
=
называется относительной магнитной
проницаемостью, т.е. В =В0
.
§ 7 – 3. Классификация магнетиков
Принято различать три класса магнетиков: диамагнетики, парамагнетики и ферромагнетики.
1.Диамагнетики. Диамагнетизм – явление универсальное. Оно обусловлено законом электромагнитной индукции. В момент включения магнитного поля элементарные молекулярные токи в веществе изменяются таким образом, чтобы воспрепятствовать возникновению внешнего поля, т.е. индуцированный дополнительный магнитный момент направлен против внешнего поля. Суммарное действие всех элементарных индуцированных моментов приводит к тому, что внешнее магнитное поле В0 уменьшается: В = В0 – В инд . Это означает, что
= (1+ ) 1 или 0. Величина диам крайне незначительна и составляет около 10 –4 – 10-5.
2.Парамагнетики. К парамагнетикам относятся вещества, атомы которых имеют незаполненные электронные оболочки, причем число электронов на них должно быть нечетно. Тогда каждый атом можно рассматривать как элементарный молекулярный ток, магнитный момент которого ориентируется вдоль направления внешнего поля., т.е. В = В0 +Всобст .Очевидно, что для этих веществ 0. Значения парам достигают величины порядка 10 –3.
3.Ферромагнетики. В этих веществах между отдельными атомами возникает особый вид взаимодействия, имеющий сугубо квантовомеханическое происхождение и поэтому нами не рассматриваемый. Это взаимодействие носит название обменного. Благодаря этому взаимодействию в ферромагнетиках возникают малые, но конечные области – так называемые домены, где все атомные магнитные моменты оказываются упорядоченными так, что каждый домен намагничен. Однако в макроскопическом объеме взятого образца домены ориентированы хаотически, и суммарный магнитный момент всего образца равен нулю. Внешнее магнитное поле стремится ориентировать все домены в одном направлении – образец намагничивается. Характерной особенностью ферромагнетиков является то, что собственное магнитное поле значительно превышает внешнее, т.е. для них 1 ( для некоторых сплавов железа 10 6 .
§ 7-4. Магнитное поле Земли
Известно, что планета Земля представляет собой гигантский постоянный магнит, северный полюс которого находится в южном полушарии Земли, а южный – на севере Канады, примерно в 1500 км от северного географического полюса. Несовпадение магнитных и географических полюсов приводит к тому, что стрелка компаса не указывает точно на полюс. Это явление известно как склонение. Для Москвы склонение – восточное, оно составляет 6,50. Установлено, что магнитное поле Земли оказывает влияние на сезонные миграции зверей и птиц . Менее известным фактом является то, что поле Земли защищает все живое на планете от убийственного действия космической радиации, создавая вокруг планеты радиационные пояса. Нижний радиационный пояс находится на высоте 200–600 км, тогда как верхний постирается до 1500 км. Кроме того, магнитное поле Земли отклоняет потоки частиц от Солнца в области, прилегающие к полюсам, вызывая полярные сияния.
Переменный ток. Тема 8.
§ 8 – 1. Получение переменного тока
Рис.28. Схема устройства электрогенератора. |
|
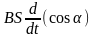 ,
где - угол между
направлением магнитного поля В и нормалью
к площади рамки S. Направление
тока в рамке в выбранный момент времени
определяется по правилу правой руки.
Нетрудно видеть, что направление токов
в верхнем и нижнем проводниках
противоположны друг другу. Концы рамки
подключаются к кольцам, которые, в свою
очередь, с помощью скользящих контактов
подсоединены к выходным клеммам
генератора. В мощных генераторах рамка
содержит несколько десятков или сотен
витков, токи в ней достигают значительной
величины, поэтому сама рамка делается
неподвижной, чтобы избежать трущихся
контактов, а магнитная система вращается
вокруг рамки. Частота вращения является
государственным стандартом: в США это
60Гц , в Росси –50 Гц.
,
где - угол между
направлением магнитного поля В и нормалью
к площади рамки S. Направление
тока в рамке в выбранный момент времени
определяется по правилу правой руки.
Нетрудно видеть, что направление токов
в верхнем и нижнем проводниках
противоположны друг другу. Концы рамки
подключаются к кольцам, которые, в свою
очередь, с помощью скользящих контактов
подсоединены к выходным клеммам
генератора. В мощных генераторах рамка
содержит несколько десятков или сотен
витков, токи в ней достигают значительной
величины, поэтому сама рамка делается
неподвижной, чтобы избежать трущихся
контактов, а магнитная система вращается
вокруг рамки. Частота вращения является
государственным стандартом: в США это
60Гц , в Росси –50 Гц.
§ 8 –2. Квазистационарные токи
Квазистационарным называется переменный ток, для которого в любой момент времени оказывается справедливым закон Ома, сформулированный ранее для постоянного тока. Это означает, что в неразветвленных цепях сила тока, проходящего через любой элемент цепи, в данный момент времени одинакова для всех элементов. Неквазистационарными токи становятся тогда, когда частота колебаний достигает очень больших значений – таких, что соответствующая им длина волны = сТ, где с –скорость света, а Т –период колебаний, становится сравнимой с геометрическими размерами цепи. Например, для промышленного тока 50 Гц эта длина волны равна 6000 км.
В прошлом семестре было показано, что на длине волны амплитуды колебаний в разных точках пространства различны, изменяясь от максимума до нуля и наоборот через каждые /4. Поэтому мгновенные значения ока будут одинаковы тогда, когда l , где l – длина цепи.
|
|
§ 8 –3. Закон Ома для переменного тока
Рассмотрим цепь, состоящую из омического сопротивления, катушки индуктивности и конденсатора. Пусть все они соединены друг с другом последовательно и подключены к источнику переменного тока с ЭДС E (см. рис. 29). Формально эта цепь разомкнута, и ее концами являются обкладки конденсатора, поэтому для нее можно написать закон Ома для участка цепи, содержащей ЭДС, полагая, что условие квазистационарности выполнено. Тогда
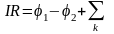 Ek
, ( ХХ)
Ek
, ( ХХ)
где
 = UC
- напряжение на конденсаторе, а суммарная
ЭДС складывается из ЭДС источника тока
и ЭДС самоиндукции EL
:
= UC
- напряжение на конденсаторе, а суммарная
ЭДС складывается из ЭДС источника тока
и ЭДС самоиндукции EL
:
 Ek
= EL
+ E
(t), EL
= -
.
Ek
= EL
+ E
(t), EL
= -
.
Обычно величину называют падением напряжения на индуктивности и обозначают UL , т.е. UL= , произведение IR =UR –падением напряжения на сопротивлении. С учетом этого уравнение (ХХ) можно преобразовать:
UR + UL + UC = E (t). (ХХХ)
Вспоминая, что
 и заменяя величины UC
и UL
, получим
и заменяя величины UC
и UL
, получим
 E
(t). ()
E
(t). ()
Предположим, что ток в нашей цепи изменяется по синусоидальному закону: I = I0 sint.
Тогда UR = I0R sint , UL = LI0 cost = LI0 sin(t -/2),
=
 .
.
Эти соотношения
должны быть справедливыми в любой момент
времени, поэтому они справедливы и для
амплитудных значений, т.е.
 .
.
Рис.30. Векторная диаграмма для последовательной цепи. |
|
 аналогичны по своему значению сопротивлению
R. Используя такую
интерпретацию, можно видеть, что уравнение
() приобретает
тригонометрический смысл: напряжения
на емкости и индуктивности оказываются
сдвинутыми по фазе на /2
относительно напряжения на сопротивлении
R. Здесь удобнее использовать векторное
представление колебаний, которое
рассматривалось в прошлом семестре.
Любое гармоническое колебание y(t)
= Asin( t
+ )
можно представить в векторном виде:
длина вектора определяется амплитудой
колебаний А, начальная фаза определяет
угол отклонения вектора от горизонтальной
оси, а - частоту, с
которой вектор вращается вокруг начала
координат. В этом представлении напряжение
на сопротивлении R
изображается в виде горизонтально-
аналогичны по своему значению сопротивлению
R. Используя такую
интерпретацию, можно видеть, что уравнение
() приобретает
тригонометрический смысл: напряжения
на емкости и индуктивности оказываются
сдвинутыми по фазе на /2
относительно напряжения на сопротивлении
R. Здесь удобнее использовать векторное
представление колебаний, которое
рассматривалось в прошлом семестре.
Любое гармоническое колебание y(t)
= Asin( t
+ )
можно представить в векторном виде:
длина вектора определяется амплитудой
колебаний А, начальная фаза определяет
угол отклонения вектора от горизонтальной
оси, а - частоту, с
которой вектор вращается вокруг начала
координат. В этом представлении напряжение
на сопротивлении R
изображается в виде горизонтально-
го вектора (см. рис.30), а напряжения на емкости и индуктивности оказываются повернутыми относительно него в разные стороны на 900 . В последовательной цепи действующее в ней общее напряжение складывается из падения напряжений на всех участках. Поэтому оно может быть найдено как геометрическая сумма падения напряжений на индуктивности, емкости и сопротивления. Тогда согласно теореме Пифагора можно записать, что
 ,
,
или, выражая UR , UL и UC через произведения тока на соответствующие сопротивления,
 .
.
Извлекая квадратный корень из обеих частей последнего равенства, получим:
 .
()
.
()
При выводе этого выражения учтено, что для последовательной цепи IR = IL= IC =I. Полученное выражение по своей структуре аналогично закону Ома для цепи постоянного тока. Поэтому оно называется законом Ома для переменного тока. Важно отметить, что между током и напряжением существует сдвиг фаз, величина которого определяется из рис.30:
 или
или
 .
.
§ 8 – 4. Мощность переменного тока
Значение мгновенной
мощности W определим по
аналогии с законом Джоуля – Ленца для
постоянного тока: W =IU
= I0U0
sint
sin(t
+).
Однако, с практической точки зрения
более полезно вычислить среднюю мощность
за единицу времени. Определим среднее
значение за время одного колебания
любой переменной величины y(t)
как интеграл, средний за период:
 .
Тогда
.
Тогда
 =
=
=
+ = -
= -
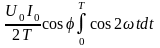 +
+
+ .
.
Интегралы
в последнем выражении все равны
нулю, т.к. среднее значение за период
лю-бой периодической величины равно
нулю.Поэтому
 ,
где Uэфф=
,
где Uэфф=
 ;
Iэфф =
;
Iэфф = - так называемые эффективные значения
напряжения и тока.
- так называемые эффективные значения
напряжения и тока.
Формула мощности для переменного тока отличается от аналогичной формулы для постоянного тока лишь коэффициентом cos , который принято называть коэффициентом мощности. Увеличение этого коэффициента является важной практической задачей. Там, где сдвиг фаз между током и напряжением достигает 900 , средняя мощность оказывается равной нулю.
Колебательный контур. Тема 9.
§ 9 –1. Затухающие колебания в колебательном контуре
Рассмотрим последовательную цепь, содержащую катушку индуктивности L, емкость С, сопротивление R и ключ. Предположим, что на емкости в начальный момент времени имеется некоторый заряд . Если цепь замыкается, то в цепи возникает электрический ток. Наличие катушки индуктивности обуславливает возникновение ЭДС самоиндукции, которая своим действием препятствует возрастанию разрядного тока конденсатора. В тот момент, когда напряжение на конденсаторе становится равным нулю, ток через индуктивность достигает максимума. В дальнейшем ЭДС самоиндукции стремится поддержать этот ток, что приводит к перезарядке конденсатора до некоторого напряжения обратной полярности. Процесс перезарядки конденсатора повторяется определенное число раз в зависимости от величины потерь энергии на сопротивлении. Способность контура к перезарядке характеризуется качеством контура или добротностью. Добротность контура Q определяется отношением энергии, запасенной на конденсаторе или в катушке индуктивности, к величине потерь энергии на сопротивлении за период:

Для количественного описания процессов в последовательном колебательном контуре используется уравнение, полученное ранее при рассмотрении переменного тока:
E (t), ( ++)
с той разницей, что в нашем случае внешняя ЭДС отсутствует так, что уравнение принимает вид:
0.
Введем обозначения
: ; =
; =
 и учтем, что по определению I=
и учтем, что по определению I= .Тогда
наше уравнение принимает вид, знакомый
по курсу прошлого семестра:
.Тогда
наше уравнение принимает вид, знакомый
по курсу прошлого семестра:

где в качестве
переменной выступает заряд q.
Решением этого дифференциального
уравнения служит функция q(t)
= q0 e
-t
cos(t
+ ),
где величины q0 и
определяются начальными условиями
,
а 2
=
 с учетом того, что в большинстве случаев
0
. Очевидно, что при
= 0 колебания в контуре становятся
незатухающими, и частота этих колебаний
равна
с учетом того, что в большинстве случаев
0
. Очевидно, что при
= 0 колебания в контуре становятся
незатухающими, и частота этих колебаний
равна
 .
Добротность контура Q
может быть выражена через его параметры.
Энергия, запасенная в индуктивности,
равна L
.
Добротность контура Q
может быть выражена через его параметры.
Энергия, запасенная в индуктивности,
равна L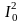 /2.,
а мощность, выделяемая на сопротивлении,
-
/2.,
а мощность, выделяемая на сопротивлении,
-
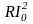 /2.
За период Т =
/2.
За период Т = на сопротивлении выделится энергия
R
T/2
=
на сопротивлении выделится энергия
R
T/2
= 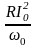 .
Поэтому Q = 2
.
Поэтому Q = 2 .
.
Как видно из полученного выражения, величина добротности определяется лишь параметрами контура L,C и R.
§ 9 –2. Вынужденные колебания в контуре. Резонанс
Включим в цепь рассматриваемого контура внешнюю переменную ЭДС
E = E0 sin(t+).
Повторяя процедуру прошлого семестра, найдем графическое решение уравнения (++). Будем искать решение уравнения
 в
виде q(t) =
q0sin
t.
Тогда
в
виде q(t) =
q0sin
t.
Тогда
 .
.
Подставляя эти величины в исходное уравнение, имеем:
 .
.
Рис.31.Графическое решение дифференциального уравнения. |
|

откуда
 (Р)
(Р)
Из
полученного выражения видно, что
амплитуда заряда на конденсатора
изменяется в зависимости от частоты
внешней ЭДС, достигая максимума, когда
подкоренное выражение минимально. Это
достигается тогда, когда
 ;
если 0 ,
то Р
0
;
если 0 ,
то Р
0
Рис.32. Резонансная кривая. |
|
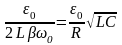 ,
и напряжение на конденсаторе
,
и напряжение на конденсаторе
 (*)
(*)
в Q раз больше, чем напряжение внешней ЭДС. Графическая зависимость напряжения на
конденсаторе UC
от частоты представлена на рис.32. Важной
технической характеристикой контура
является полоса пропускания, которая
определяется как область частот ,где
энергия, запасаемая в контуре на частоте
, отличается от
энергии на частоте 0
в наименьшее целое число раз (в два).
Обычно  .На
границах области
.На
границах области =0
=0
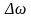 ..При
этих условиях
..При
этих условиях

 .
Из этого соотношения следует, что
=. Тогда напряжение
на емкости можно записать так:
.
Из этого соотношения следует, что
=. Тогда напряжение
на емкости можно записать так:
 .
.
Сравнивая
это выражение с формулой (*), можно
заметить, что Q =
 .
Последняя формула имеет важный
практический смысл. Она позволяет
рассчитать добротность из экспериментально
полученной резонансной кривой. Для
этого достаточно провести горизонтальную
прямую на уровне
.
Последняя формула имеет важный
практический смысл. Она позволяет
рассчитать добротность из экспериментально
полученной резонансной кривой. Для
этого достаточно провести горизонтальную
прямую на уровне
 qрез
до пересечения с резонансной кривой
и спроектировать точки пересечения на
ось частот. Этот интервал и определит
полосу пропускания.
qрез
до пересечения с резонансной кривой
и спроектировать точки пересечения на
ось частот. Этот интервал и определит
полосу пропускания.
Колебательные контуры широко применяются в телевизорах, радиоприемниках, передатчиках, в различных радиоустройствах избирательного действия и т.п. Мы же рассмотрим более подробно одно из атмосферных явлений, которое можно представить как разряд конденсатора в колебательном контуре. Это явление – гроза, точнее возникновение молнии.
§ 9 –3. Простейшая теория грозы
Рис.33. Структура грозового облака. |
|
Дождь, как известно, обусловлен тем, что вертикальные потоки нагретого влажного воздуха переносят влагу в верхние слои атмосферы, где водяные пары конденсируются в мельчайшие капельки. Током воздуха капельки увлекаются вверх, постепенно увеличиваясь в своих размерах. Объем (вес) капельки растет пропорционально кубу ее радиуса, тогда как подъемная сила воздушного потока пропорциональна всего лишь квадрату радиуса капли. Поэтому наступает момент, когда капля перестает подниматься и начинает падать. При падении капли образуют целый поток, который выталкивает перед собой холодный воздух из верхних слоев атмосферы. Когда капли достигают поверхности Земли, образуется дождь. Началу дождя предшествует холодный вихрь. Возникновение же грозы зависит от того, переносят капли электрический заряд или не переносят. Описание механизма переноса заряда предложено американским ученым Вильямсом. Согласно его гипотезе все определяется структурой грозового облака. Полеты самолетов внутрь таких облаков показали, ионы, тогда как положительные ионы отталкиваются. Верхняя же часть капли оказывает на ионы меньшее влияние. В результате капли притягивают отрицательные тоны и приобретают отрицательный заряд. Положительный же заряд переносится в верхнюю часть тучи и постепенно переходит в ионосферу. Накопление заряда в различных частях грозового облака приводит к появлению огромной разности потенциалов, достигающей 100 млн вольт. Эта разность потенциалов может образовываться как между различными облаками, так и между облаком и земной поверхностью. Рассмотрим второй случай. По мере накопления заряда в нижней части облака вблизи его нижней кромки образуется электрическое поле, которое ионизирует воздух. Поле различно в разных точках, поэтому и степень поляризации будет различной. Там, где воздух ионизируется полностью, образуется новое состояние вещества – плазма. Плазма начинает светиться и для уменьшения потерь энергии на излучение стремится образовать шарообразную форму. Внешне это выглядит так: из тучи внезапно вываливается небольшой светящийся комок, получивший название белого лидера, и устремляется к Земле. Скорость его движения достигает 50 000 км/сек. Но лидер двигается с остановками, во время которых может произойти его деление. Движение лидера подготавливает канал для основного разряда. Если лидер делится, то возможно ветвление разряда. Когда до Земли остается около 100 метров, с земной поверхности навстречу лидеру поднимается заряд, стремящийся двигаться вдоль острых высоких предметов. При смыкании лидера с этим зарядом образуется канал, по которому отрицательный заряд попадает на Землю. Образуется гигантская искра, но длительность этого искрового разряда мала. Через доли секунды из тучи выходит новый комок – так называемый темный лидер. Он с большой скоростью и без остановки устремляется к Земле по подготовленному каналу. Вслед за ним идет основной разряд. Искра возникает снова. Темный лидер может образовываться несколько раз, вызывая несколько ударов молнии (рекорд – 42 раза).
Каждый удар молнии переносит до 40 Кулонов, но отрицательный заряд не удерживается на Земле. Между земной поверхностью и ионосферой существует разность потенциалов около 400 киловольт, поэтому в атмосфере постоянно идет ток, направленный вверх. Его плотность мала – несколько микроампер на кв. метр ( 1 мкА = 10 –6 А), но общее значение тока достигает 1800 Ампер. Мощность, развиваемая в такой цепи, превышает 700 Мегаватт. Грозы лишь компенсируют утечку заряда. Ежесекундно на Земле происходит около 300 гроз. Средний разрядный ток в них также равен 1800 Ампер, обеспечивая неизменность заряда Земли.
§ 9 –4. Теория Максвелла
Рассмотрим проводящий виток, помещенный в изменяющееся магнитное поле. По закону Фарадея в витке возникает ЭДС индукции. Направление индукционного тока таково, что он своим действием препятствует изменению магнитного поля. Если внешнее магнитное поле возрастает, его изменение В направлено по полю (см. рис.34), и направление индукционного тока должно быть таким, чтобы магнитный момент витка Iинд S был направлен против поля
Рис.34. Направление индукционного тока. |
|
 ;
;
Ф = .
Если виток не изменяет своей формы, то знак производной можно внести под знак интеграла. Тогда получим:
E = - ,
,
где наклонные
 означают частную производную
(предполагается, что значения В могут
зависеть от времени и координат). Согласно
своему определению ЭДС характеризует
работу, совершаемую сторонними силами
по всему замкнутому контуру (витку),
т.е. E
=
,
где Е представляет собой напряженность
сторонних сил, создающих индукционный
ток. Виток замкнут и однороден, поэтому
силовые линии электрического поля тоже
должны быть замкнутыми, т.е. индуцированное
в проводнике электрическое поле является
вихревым. Максвелл предположил, что
наличие проводника не является
обязательным: силовые линии электрического
поля останутся замкнутыми и в свободном
пространстве. На основании этого он
сделал вывод, что всякое изменяющееся
во времени магнитное поле порождает
вокруг себя вихревое электрическое
поле. Это положение называют первой
гипотезой Максвелла, Закон Фарадея
теперь записывается так:
означают частную производную
(предполагается, что значения В могут
зависеть от времени и координат). Согласно
своему определению ЭДС характеризует
работу, совершаемую сторонними силами
по всему замкнутому контуру (витку),
т.е. E
=
,
где Е представляет собой напряженность
сторонних сил, создающих индукционный
ток. Виток замкнут и однороден, поэтому
силовые линии электрического поля тоже
должны быть замкнутыми, т.е. индуцированное
в проводнике электрическое поле является
вихревым. Максвелл предположил, что
наличие проводника не является
обязательным: силовые линии электрического
поля останутся замкнутыми и в свободном
пространстве. На основании этого он
сделал вывод, что всякое изменяющееся
во времени магнитное поле порождает
вокруг себя вихревое электрическое
поле. Это положение называют первой
гипотезой Максвелла, Закон Фарадея
теперь записывается так:
 .
( I )
.
( I )
Кроме этого существует второе положение теории Максвелла, которое вытекает из рассмотрения теоремы о циркуляции магнитного поля. Как было показано, циркуляция магнитного поля имеет следующий вид:
 .
.
Рис.35. К выводу теоремы о полном токе. |
|
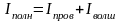 .
.
В проводниках I пров = Iполн , а в пространстве между пластинами Iполн = Iволш . Нетрудно видеть, что при этих условиях теорема о циркуляции справедлива везде.
Обратимся к рассмотрению «волшебного тока» внутри пластин конденсатора. Мы знаем, что ток I пров =dQ/dt. На конденсаторе Q = S ( - плотность поверхностных зарядов, а S – площадь пластин конденсатора). Напряженность электрического поля внутри конденсатора равна E = /0 или D0 = , где D0 = 0 E – вектор электрического смещения. С учетом этого запишем

В то же время очевидно, что I пров = Iволш, поэтому последний ток Максвелл назвал током смещения. Теперь теорема о циркуляции принимает новый вид, где под знаком суммы стоит полный ток Iполн:
 .
.
Для проводников произвольного сечения и для произвольной формы пластин конденсатора токи выражаются через соответствующее суммирование плотности токов:
Iпров
=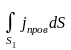 ; I смещ =
; I смещ =
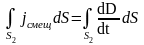 ,
,
так что теорема о полном токе приобретает следующий вид:

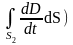 .
(II)
.
(II)
Если проводники отсутствуют, ток проводимости равен нулю, и уравнение (II) имеет вид:
 .
(III)
.
(III)
|
|
Уравнения (I)
и (II) называются уравнениями
Максвелла. Вместе с уравнениями
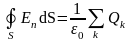 и
.
и
.
они составляют так называемую систему уравнений Максвелла, полностью описывающую свойства электрического и магнитного полей.
§ 9 –5. Электромагнитные волны
Из уравнений Максвелла вытекает вывод о существовании электромагнитных волн. Для того, чтобы показать это, рассмотрим уравнения (I) и (III) в применении к конкретным полям. Пусть имеется некоторая система координат Х,Y,Z, как показано на рис.36, и в начале координат какими-то внешними причинами созданы электрическое и магнитное поля, характеризующиеся векторами Е иВ соответственно. Направления этих векторов указаны на рис. Выберем малые прямоугольники со сторонами dx, dy и dz (см. рис.36) Вычислим циркуляции векторов Е и В по периметру прямоугольников. Для вычисления используем тот же прием, с помощью которого была определена величина вектора магнитной индукции на оси длинного соленоида. Направление обхода контуров выберем по часовой стрелке, и учтем, что величины Е и В могут зависеть от х. На расстоянии dx от начала координат они принимают значения Е + dЕ и В + dВ соответственно. При этих условиях
 или
или
 .
.
Аналогично для вектора В
 .
.
Значения (E+dE)dy и Bdz взяты со знаком минус потому, что вектора на соответствующих отрезках направлены против выбранного обхода контуров. Подставляя вычисленные значения циркуляции в уравнения (I) и (III), получим:
 и
и
 ,
откуда
,
откуда
 ;
;
 ,
где производная по х имеет смысл
частной производной, поэтому правильнее
заменить знак
,
где производная по х имеет смысл
частной производной, поэтому правильнее
заменить знак
 на знак частной производной
на знак частной производной
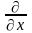
 ;
;
 .
.
Дифференцируя первое уравнение по х, а второе – по t, и сравнивая полученные результаты, имеем:
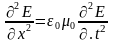 .
.
Из курса механики известно, что это уравнение относится к так называемым волновым уравнениям, решению которых соответствует бегущая волна. Скорость распространения волны определяется коэффициентом, стоящим перед второй производной по времени:
 .
.
Аналогичное уравнение может быть получено и для вектора магнитной индукции В.Из уравнений (I) и (III) следует, что электрический и магнитный вектора связаны между собой, поэтому волны названы электромагнитными. Подставляя численные значения 0 и 0 , получим, что v = c = 3108 м/c, т.е. скорость распространения электромагнитной волны равна скорости света. Если волна распространяется в среде, характеризующейся постоянными и , то скорость электромагнитной волны

 - показатель преломления среды относительно
вакуума.
- показатель преломления среды относительно
вакуума.
Рис.37. Структура электромагнитной волны. |
|
Это электрическое поле создает переменное магнитное, плоскость колебаний которого совпадает с плоскостью первичного магнитного поля (см. рис.37) так, что магнитное поле сохраняет свою ориентацию в пространстве. Если в любой плоскости, перпендикулярной направлению распространения, значения Е и В не зависят от координат, то волна называется плоской, и ее можно записать так:
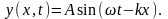
В
этом выражении
 -
волновое число,
= сТ, =2/T.
Формула плоской электромагнитной волны
будет часто использоваться при
рассмотрении оптических явлений.
Световыми являются волны, длина которых
лежит в интервале от 0,4 до 0,7 мкм. Волна,
в которой колебания имеют одну частоту,
называется монохроматической
(одноцветной). Белый свет содержит не
менее семи основных цветов. Для упрощения
математических выкладок часто
ограничиваются рассмотрением
монохроматических волн.
-
волновое число,
= сТ, =2/T.
Формула плоской электромагнитной волны
будет часто использоваться при
рассмотрении оптических явлений.
Световыми являются волны, длина которых
лежит в интервале от 0,4 до 0,7 мкм. Волна,
в которой колебания имеют одну частоту,
называется монохроматической
(одноцветной). Белый свет содержит не
менее семи основных цветов. Для упрощения
математических выкладок часто
ограничиваются рассмотрением
монохроматических волн.
Примеры решения задач
Пример 1. Тонкий стержень длиной l=30 см (рис. 38) несет равномерно распределенный по длине заряд с линейной плотностью =1 мкКл/м. На расстоянии r0=20 см от стержня находится заряд Q1=10 нКл, равноудаленный от концов, стержня. Определить силу F взаимодействия точечного заряда с заряженным стержнем.
Решение. Закон Кулона позволяет вычислить силу взаимодействия точечных зарядов. По условию задачи, один из зарядов не является точечным, а представляет собой заряд, равномерно распределенный по длине стержня. Однако если выделить на стержне дифференциально малый участок длиной dl, то находящийся на нем заряд dQ=dl можно рассматривать как точечный и тогда по закону Кулона сила взаимодействия между зарядами Q1 и dQ в вакууме:

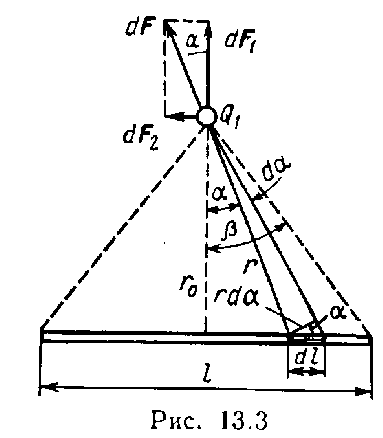 , (1)
, (1)
г
Рис. 38
де r — расстояние от выделенного элемента до заряда Q1.Из
чертежа (рис. 13.3) следует, что
 и
и
 ,
где
,
где
r0 — расстояние от заряда Q1 до стержня. Подставив эти выражения r к dl в формулу (1), получим
 . (2)
. (2)
Следует иметь в виду, что dF — вектор, поэтому, прежде чем интегрировать разложим его на две составляющие: dF1, перпендикулярную стержню, и dF2, параллельную ему.
Из рис. 13.3 видно, что dF1=dFcos,
dF2=dFsin.
Подставляя значение dF из выражения
(2) в эти формулы, найдем:

Интегрируя эти выражения в пределах от – до +, получим
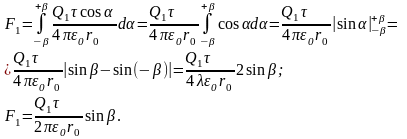
В силу симметрии расположения заряда Q1 относительно стержня интегрирования второго выражения дает нуль;
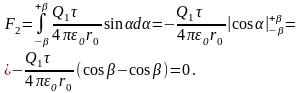
Таким образом, сила, действующая на заряд Q1,
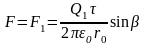 . (3)
. (3)
Из.
рис. 13.3 следует, что
 .
Подставив это выражение sin
в формулу (3), получим
.
Подставив это выражение sin
в формулу (3), получим
 . (4)
. (4)
Произведем вычисления по формуле (4):

Пример 2. Электрическое поле создано двумя точечными зарядами: Q1=30 нКл и Q2= –10 нКл. Расстояние d между зарядами равно 20 см. Определить напряженность электрического поля в точке, находящейся на расстоянии r1=15 см от первого и на расстоянии r2=10 см от второго зарядов.
Р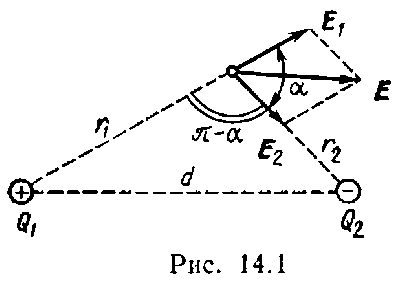 ешение.
Согласно принципу суперпозиции
электрических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность Е электрического
поля в искомой точке может быть найдена
как векторная сумма напряженностей E1
и Е2 полей, создаваемых
каждым зарядом в отдельности: E=E1+E2.
ешение.
Согласно принципу суперпозиции
электрических полей, каждый заряд
создает поле независимо от присутствия
в пространстве других зарядов. Поэтому
напряженность Е электрического
поля в искомой точке может быть найдена
как векторная сумма напряженностей E1
и Е2 полей, создаваемых
каждым зарядом в отдельности: E=E1+E2.
Рис. 39
Напряженности электрического поля, создаваемого в вакууме первым и вторым зарядами, соответственно равны (1)
(1)
Вектор E1 (рис. 39) направлен по силовой линии от заряда Q1, так как заряд Q1>0; вектор Е2 направлен также по силовой линии, но к заряду Q2, так как Q2<0.
Модуль вектора Е найдем по теореме косинусов:
 , (2)
, (2)
где угол может быть найден из треугольника со сторонами r1, r2 и d:
 .
.
В данном случае во избежание громоздких записей вычислим отдельно значение cos. По этой формуле найдем
cos =0,25.
Подставляя выражения E1 и E2 а по формулам (1) в равенство (2) и вынося общий множитель 1/(40) за знак корня, получаем
 .
.
Подставив значения величин , 0, Q1, Q2, r1-, r2 и в последнюю формулу и произведя вычисления, найдем

Пример 3. Найти работу А поля по перемещению заряда Q=10 нКл из точки 1 в точку 2 (рис. 40), находящиеся между двумя разноименно заряженными с поверхностной плотностью =0,4 мкКл/м2 бесконечными параллельными плоскостями, расстояние l между которыми равно 3 см.
Р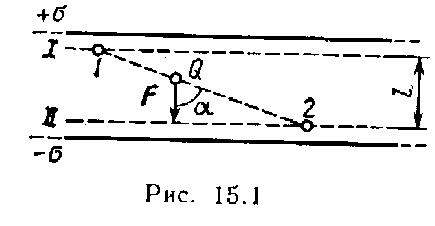 ешение.
Возможны два способа решения задачи.
ешение.
Возможны два способа решения задачи.
1
Рис.40
-й способ. Работу сил поля по перемещению заряда Q из точки 1 поля с потенциалом 1 в точку 2 поля с потенциалом 2 найдем по формулеA=Q(1—2). (1)
Для определения потенциалов в точках 1 и 2 проведем через эти точки эквипотенциальные поверхности I и II. Эти поверхности будут плоскостями, так как поле между двумя равномерно заряженными бесконечными параллельными плоскостями однородно. Для такого поля справедливо соотношение
1—2=El, (2)
где Е — напряженность поля; l — расстояние между эквипотенциальными поверхностями.
Напряженность поля между параллельными бесконечными разноименно заряженными плоскостями E=/0. Подставив это выражение Е в формулу (2) и затем выражение 1—2 в формулу (1), получим
A=Q(/0)l.
2-й способ. Так как поле однородно, то сила, действующая на заряд Q, при его перемещении постоянна. Поэтому работу перемещения заряда из точки 1 в точку 2 можно подсчитать по формуле
A=Fr cos, (3)
где F — сила, действующая на заряд; r — модуль перемещения заряда Q из точки 1 в точку 2; — угол между направлениями перемещения и силы. Но F=QE=Q(/0). Подставив это выражение F в равенство (3), а также заметив, что rcos=l, получим
A=Q(/0)l. (4)
Таким образом, оба решения приводят к одному и тому же результату.
Подставив в выражение (4) значение величин Q, , 0 и l, найдем
A=13,6 мкДж.
Пример 4. Два плоских конденсатора одинаковой электроемкости С1=С2=С соединены в батарею последовательно и подключены источнику тока с электродвижущей силой ε. Как изменится разность потенциалов U1 на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отключая источника тока, заполнить диэлектриком с диэлектрической проницаемостью ε =7?
Р е ш е н и е. До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была одинакова: U1=U2=ε/2. После заполнения электроемкость второго конденсатора возросла в ε раз:
C2'=εC2=εC.
Электроемкость С первого не изменилась, т. е. C1'=C.
Так как источник тока не отключался, то общая разность потенциалов на батарее конденсаторов осталась прежней, она лишь перераспределилась между конденсаторами. На первом конденсаторе
U1'=Q/C1'=Q/C, (1)
где Q - заряд на пластинах конденсатора. Поскольку при последовательном соединении конденсаторов заряд на каждой пластине и на всей батареи одинаков, то
Q = С'батε
где
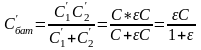 .
Таким образом,
.
Таким образом,
 ε.
ε.
Подставив это выражение заряда в формулу (1), найдем
 ε
ε ε.
ε.
Чтобы найти, как изменилась разность потенциалов на пластинах первого конденсатора, вычислим отношение:
U'1/U1=2ε/(1+ε).
После подстановки значения ε получим
U'1/U1=1,75.
Следовательно, разность потенциалов на пластинах первого конденсатора после заполнения второго конденсатора диэлектриком возросла в 1,75 раза.
Пример 5. Плоский воздушный конденсатор с площадью S пластины, равной 500 см2, подключен к источнику тока, ЭДС которого равна 300 В. Определить работу А внешних сил по раздвижению пластин от расстояния d1 = 1 см до d2=3 см в двух случаях: 1) пластины перед раздвижением отключаются от источника тока; 2) пластины в процессе раздвижения остаются подключенными к нему.
Р е ш е н и е. 1-й случай. Систему двух заряженных и отключенных от источника тока пластин можно рассматривать как изолированную систему, по отношению к которой справедлив закон сохранения энергии. В этом случае работа внешних сил равна изменению энергии системы:
A=ΔW=W2-W1, (1)
где W2 - энергия поля конденсатора в конечном состоянии (пластины находятся на расстоянии d2); W1 - энергия поля в начальном состоянии (пластины находятся на расстоянии d1).
Энергию в данном случае удобно выразить через заряд Q на пластинах, так как заряд пластин, отключенных от источника при их раздвижении, не изменяется. Подставив в равенство (1) выражения W2=Q2/ (2С2) и W1 =Q2/(2С1), получим
 ИЛИ
ИЛИ

Выразив в этой формуле заряд через ЭДС ε источника тока и начальную электроемкость С1 (Q=C1ε), найдем
 (2)
(2)
Подставляя в формулу (2) выражения электроемкостей (C1=ε0S/d1 и C2= =ε0S/d2) плоского конденсатора, получим
 ε2
ε2
После сокращения на ε0S формула примет вид
A=ε0Sε2(d2 -d1)/ 2d12 (3)
Произведя вычисления по формуле (3), найдем A= 3,98 мкДж.
2-й случай. Пластины остаются подключенными к источнику тока и система двух пластин уже не является изолированной (заряд с пластин при их раздвижении перемещается к клеммам батареи). Поэтому воспользоваться законом сохранения энергии в этом случае нельзя.
Заметим, что при раздвижении пластин конденсатора: а) разность их потенциалов остается неизменной (U=ε);б) емкость будет уменьшаться (С= ε0S/d.) Будут уменьшаться также заряд на пластинах (Q=CU) и напряженность электрического поля (Е = U/d). Так как величины Е и Q, необходимые для определения работы, изменяются, то работу следует вычислять путем интегрирования.
Напишем выражение для элементарной работы:
dA=QE1dx, (4)
где E1 - напряженность поля, создаваемого зарядом одной пластины.
Выразим напряженность поля E1 и заряд Q через расстояние х между пластинами:
E1 = 1/2 Е = ε/2х и Q = Cε, или Q = ε0Sε/x.
Подставив эти выражения E1 и Q в равенство (4), получим
dA=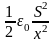 ε2dx.
ε2dx.
Проинтегрировав это равенство в пределах от d1 до d2, найдем выражение искомой работы:
 ε
ε ε2
ε2 ε2.
ε2.
После упрощений последняя формула примет вид
A=ε0S ε2(d2-d1)/(2d1d2)
Сделав вычисления по полученной формуле, найдем
А=1.33 мкДж.
Пример 6. Сила тока в проводнике сопротивлением R=20 Ом нарастает в течение времени Δt=2 с по линейному за. кону от I0=0 до Imax=6 А (рис. 41). Определить количество теплоты Q1, выделившееся в этом проводнике за первую секунду, и Q2 - за вторую, а также найти отношение этих количеств теплоты Q2/Q1.
Р е ш е н и е. Закон Джоуля - Ленца Q= I2Rt
применим в случае постоянного тока
(I =const). Если
же сила тока в проводнике изменяется,
то указанный закон справедлив для
бесконечно малого промежутка времени
и записывается в виде
е ш е н и е. Закон Джоуля - Ленца Q= I2Rt
применим в случае постоянного тока
(I =const). Если
же сила тока в проводнике изменяется,
то указанный закон справедлив для
бесконечно малого промежутка времени
и записывается в виде
dQ= I2Rdt. (1)
Здесь сила тока I является некоторой функцией времени. В нашем случае
I=kt, (2)
где k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:
k=ΔI/Δt.
С учетом равенства (2) формула (1) примет вид
dQ=k2Rt2dt. (3)
Для определения количества теплоты, выделившегося за конечный промежуток времени Δt, выражение (3) следует проинтегрировать в пределах от t1 до t2:

При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t1 =О, t2= 1 с и, следовательно,
Q1=60 Дж,
а за вторую секунду - пределы интегрирования t1= 1 с, t2=2 с и тогда
Q2=420 Дж.
Следовательно,
Q2/Q1=7,
т. е. за вторую секунду выделится теплоты в 7 раз больше, чем за первую секунду.
Пример 7. Определить скорость u (мкм/ч), с которой растет слой никеля на плоской поверхности металла при электролизе, если плотность тока j, протекающего через электролит, равна 30 А/м. Никель считать двухвалентным.
Решение. Для решения задачи воспользуемся объединенным законом Фарадея
 (1)
(1)
Будем считать, что электролитическое осаждение никеля идет равномерно по всей поверхности металла. Тогда массу т выделившегося за время t никеля можно выразить через плотность , площадь S поверхности металла и толщину h слоя никеля:
m=Sh. (2)
Силу тока 7 выразим через плотность тока и площадь поверхности металла:
I=jS. (3)
Подставив в формулу (1) выражения для массы (2) и силы тока (3), получим
 (4)
(4)
При неизменной плотности тока нарастание слоя никеля будет происходить с постоянной скоростью и, определяемой отношением толщины слоя, наращенного за некоторый интервал времени, к этому интервалу (u=h/t). Тогда из формулы (4) следует

Убедимся в том, что правая часть равенства дает единицу скорости:
![]()
При этом было учтено, что валентность Z величина неименованная (безразмерная).
Выпишем значения величин, выразив их в единицах СИ: F=9,65-104 Кл/моль (см. табл), M=58,7-1СГ3 кг/моль (см. Периодическую систему элементов Д. И. Менделеева), Z=2, j=30 А/м2, p=8,8-103 кг/м3 (см. табл. плотностей)
Подставим числовые значения и произведем вычисления:
![]()
П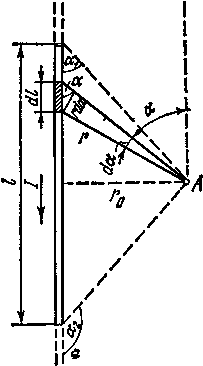 ример
8. Определить магнитную
индукцию В поля,
создаваемого отрезком бесконечно
длинного прямого провода, в точке,
равноудаленной от концов отрезка и
находящейся на расстоянии r0=20
см от середины его
(рис. 42). Сила тока I,
текущего по проводу, равна 30 А, длина
l
отрезка равна 60 см.
ример
8. Определить магнитную
индукцию В поля,
создаваемого отрезком бесконечно
длинного прямого провода, в точке,
равноудаленной от концов отрезка и
находящейся на расстоянии r0=20
см от середины его
(рис. 42). Сила тока I,
текущего по проводу, равна 30 А, длина
l
отрезка равна 60 см.
Решение. Для определения магнитной индукции поля, создаваемого отрезком провода, воспользуемся законом Био — Савара— Лапласа:
![]() (1)
(1)
Рис. 42
Прежде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу . Выразим длину элемента dl проводника через d. Согласно рис. 42, запишем ![]()
Подставим это выражение dl в формулу (1):
![]()
Но
r
— величина переменная, зависящая от
и равная
 Подставив r
в предыдущую формулу,
найдем
Подставив r
в предыдущую формулу,
найдем
![]() (2)
(2)
Чтобы определить магнитную индукцию поля, создаваемого отрезком проводника, проинтегрируем выражение (2) в пределах от 1 до 2:

Заметим, что при симметричном расположении точки A относительно отрезка провода cos 2= – cos 1. С учетом этого формула (3) примет вид
![]()
Из рис. 42 следует
![]()
Подставив выражение cos 1 в формулу (4), получим
![]()
Подставим числовые значения в формулу (5) и произведем вычисления:
![]()
Пример 9. Альфа-частица прошла ускоряющую разность потенциалов U=104 В и влетела в скрещенные под прямым углом электрическое (E=10 кВ/м) и магнитное (B=0,1 Тл) поля. Найти отношение заряда альфа-частицы к ее массе, если, двигаясь перпендикулярно обоим полям, частица не испытывает отклонений от прямолинейной траектории.
Решение. Для того чтобы найти отношение заряда Q альфа-частицы к ее массе m, воспользуемся связью между работой сил электрического поля и изменением кинетической энергии частиц:
QU=m2/2,
откуда
Q/m=2/(2U). (1)
Скорость альфа-частицы найдем из следующих соображений. В скрещенных электрическом и магнитном полях на движущуюся заряженную частицу действуют две силы:
а) сила Лоренца Fл=Q[vВ], направленная перпендикулярно скорости v и вектору магнитной индукции В;
б) кулоновская сила FK=QE, сонаправленная с вектором напряженности Е электростатического поля (Q>0).
Сделаем рисунок с изображением координатных осей и векторных
величин. Направим вектор магнитной индукции В вдоль оси Оz (рис. 43), скорость v—в положительном направлении оси Ох, тогда Fл и Fk будут направлены так, как это указано на рисунке.
Альфа-частица не будет испытывать отклонения, если геометрическая сумма сил Fл+Fk будет равна нулю. В проекции на ось

Рис. 43
Оу получим следующее равенство (при этом учтено, что вектор скорости v перпендикулярен вектору магнитной индукции В и Sin (vB)=l):
QE—QB = O,
откуда
=E/B.
Подставив это выражение скорости в формулу (1), получим
Q/m=E2( 2UB2).
Убедимся в том, что правая часть равенства дает единицу отношения заряда к массе (Кл/кг):
![]()
Произведем
вычисления:
![]()
Пример 10. На стержень из немагнитного материала длиной l=50 см намотан в один слой провод так, что на каждый сантиметр длины стержня приходится 20 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока I в обмотке равна 0,5 А. Площадь S сечения стержня равна 2 см2.
Решение. Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течет ток I, выражается формулой
 .
(1)
.
(1)
Индуктивность
соленоида в случае немагнитного
сердечника зависит только от числа
витков на единицу длины и от объема V
сердечника: L=μ0n2V,
где μ0 —магнитная постоянная.
Подставив выражение индуктивности
L в формулу (1), получим .
Учтя, что V=lS,
запишем
.
Учтя, что V=lS,
запишем
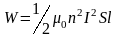 .
(2)
.
(2)
Сделав вычисления по формуле (2), найдем
W=126 мкДж.
Пример 11. Определить индукцию В и напряженность Н магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей N=200 витков, идет ток I=5 А. Внешний диаметр d1 тороида равен 30 см, внутренний d2= 20 см.
Решение.
Для определения напряженности магнитного
поля внутри тороида вычислим циркуляцию
вектора Н вдоль линии магнитной
индукции поля:

Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и что во всех точках этой линии напряженности одинаковы. Поэтому в выражении циркуляции напряженность Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2 r, где r — радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т. e.
 (1)
(1)
С другой стороны, в соответствии с законом полного тока циркуляция вектора напряженности магнитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция:
 (2)
(2)
Приравняв правые части равенств (1) и (2), получим
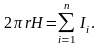 (3)
(3)
Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид 2rH=-NI, откуда
 (4)
(4)
Для средней линии тороида r=1/2(R1R2)=1/4(d1+d2). Подставив это выражение r в формулу (4), найдем
 (5)
(5)
Магнитная индукция В0 в вакууме связана с напряженностью поля соотношением B0=0H. Следовательно,
 (6)
(6)
Подставив значения величин в выражения (5) и (6), получим:
H=1,37 кА/м, B0=1,6 мТл.
Пример 12. Обмотка соленоида состоит из одного слоя плотно прилегающих друг к другу витков медного провода диаметром d=0,2 мм. Диаметр D соленоида равен 5 см. По соленоиду течет ток I=1 А. Определить количество электричества Q, протекающее через обмотку, если концы ее замкнуть накоротко. Толщиной изоляции пренебречь.
Решение. Возможны два способа решения, 1-й способ. Количество электричества dQ, которое протекает по проводнику за время dt при силе тока I, определяется равенством
![]() (1)
(1)
Полное
количество электричества, протекающее
через проводник за время t, будет
 .
Сила тока в данном случае убывает
экспоненциально со временем и выражается
формулой
.
Сила тока в данном случае убывает
экспоненциально со временем и выражается
формулой
![]()
Внося выражение силы тока I под знак интеграла и интегрируя от 0 до (при tI0), получим

Подставим пределы интегрирования и определим количество электричества, протекающее через обмотку:
![]() (2)
(2)
2-й
способ. Подставив в формулу (1) вместо
силы тока I выражение ее через
ЭДС индукции
 ,
и сопротивление R
соленоида, т. е.
,
и сопротивление R
соленоида, т. е.
![]()
Но связана со скоростью изменения потокосцепления по закону Фарадея —Максвелла: =-d/dt, тогда
![]()
Интегрируя, получаем
![]() (3)
(3)
Потокосцепление пропорционально силе тока в соленоиде. Следовательно, 1=LI0; 2=0, так как 2 соответствует тому моменту, когда ток в цепи обратится в нуль. Подставив выражения 1 и 2 в формулу (3), получим Q=1/R, или
![]()
что совпадает с формулой (2). Для определения заряда, протекающего через обмотку соленоида, следует найти индуктивность L соленоида и сопротивление R обмотки соленоида, которые выражаются формулами
![]()
где 0 — магнитная постоянная; N — число витков; l1 — длина соленоида; S1 — площадь сечения соленоида; — удельное сопротивление провода; l—длина провода; S—площадь сечения провода; d—диаметр провода; d1—диаметр соленоида.
Подставив найденные выражения L и R в формулу (2), получим
![]()
Заметим, что длина провода l может быть выражена через диаметр d1 соленоида соотношением l=d1 N, где N — число витков, тогда формуле (4) можно придать вид
![]()
Но l1/N есть диаметр провода, так как витки плотно прилегают друг к другу. Следовательно,
![]()
Произведя вычисления по формуле (5), получим
Q=363 мкКл.
Контрольная работа №2
Вариант 0
Два шарика массой m=0,l г каждый подвешены в одной точке на нитях длиной L=20 см каждая. Получив одинаковый заряд, шарики разошлись так, что нити образовали между собой угол =60°. Найти заряд каждого шарика.
На некотором расстоянии а=5 см от бесконечной проводящей плоскости находится точечный заряд Q=l нКл. Определить силу F, действующую на заряд со стороны индуцированного им заряда на плоскости.
При перемещении заряда Q=20 нКл между двумя точками поля внешними силами была совершена работа А=4 мкДж. Определить работу A1 сил поля и разность Δφ потенциалов этих точек поля.
Три одинаковых плоских конденсатора соединены последовательно. Электроемкость С такой батареи конденсаторов равна 89 пФ. Площадь S каждой пластины равна 100 см2. Диэлектрик - стекло. Какова толщина d стекла?
Расстояние d между пластинами плоского конденсатора равно 2 см, разность потенциалов U=6 кВ. Заряд Q каждой пластины равен 10 нКл. Вычислить энергию W поля конденсатора и силу F взаимного притяжения пластин.
К зажимам батареи аккумуляторов присоединен нагреватель. ЭДC ε батареи равна 24 В. Внутреннее сопротивление r=1 Ом. Нагреватель, включенный в цепь, потребляет мощность P=80 Вт. Вычислить силу тока I в цепи и КПД η нагревателя.
Д
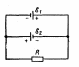 ве
батареи аккумуляторов (ε1=10
В, r1=1 Ом; ε2=8
В, r2=2 Ом) и
реостат (R=6 Ом) соединены, как
показано на рис. Найти силу тока в
батареях и реостате.
ве
батареи аккумуляторов (ε1=10
В, r1=1 Ом; ε2=8
В, r2=2 Ом) и
реостат (R=6 Ом) соединены, как
показано на рис. Найти силу тока в
батареях и реостате.
Две электролитические ванны соединены последовательно. В первой ванне выделилось m1=3,9 г цинка, во второй за то же время m2=2,24 г железа. Цинк двухвалентен. Определить валентность железа.
Найти магнитную индукцию в центре тонкого кольца, которому идет ток I=10 А. Радиус r кольца равен 5 см.
Определить частоту п вращения электрона по круговой орбите в магнитном поле, индукция В которого равна 0,2 Тл.
Вариант 1
Даны два шарика массой m=l г каждый. Какой заряд Q нужно сообщить каждому шарику, чтобы сила взаимного отталкивания зарядов уравновесила силу взаимного притяжения шариков по закону тяготения Ньютона? Рассматривать шарики как материальные точки.
Большая плоская, пластина толщиной d=1 см несет заряд, равномерно распределенный: по объему с объемной плотностью р=100 нКл/м3. Найти напряженность E электрического поля: вблизи центральной части пластины вне ее, на малом расстоянии от поверхности.
Поле создано точечным зарядом Q=1 нКл. Определить потенциал φ поля в точке, удаленной от заряда на расстояние r=20 см.
Конденсатор электроемкостью С1=0,6 мкФ был заряжен до разности потенциалов U1=300 В и соединен со вторым конденсатором электроемкостью С2=0,4 мкФ, заряженным до разности потенциалов U1=150 В. Найти заряд ΔQ, перетекший с пластин первого конденсатора на второй.
Какое количество теплоты Q выделится при разряде плоского конденсатора, если разность потенциалов U между пластинами равна 15 кВ, расстояние d=1 мм, диэлектрик - слюда и площадь S каждой пластины равна 300 см2?
Э
 ДС
батареи аккумуляторов ε
=12 В, сила тока I
короткого замыкания равна 5 А.
Какую наибольшую мощность Рmax
можно получить во внешней цепи,
соединенной с такой батареей?
ДС
батареи аккумуляторов ε
=12 В, сила тока I
короткого замыкания равна 5 А.
Какую наибольшую мощность Рmax
можно получить во внешней цепи,
соединенной с такой батареей?
Два источника тока (ε1= 8 В, r1=2 Ом; ε2=6 В, r2= 1,5 Ом) и реостат (R=10 Ом) соединены, как показано на рис. Вычислить силу тока I, текущего через реостат.
Определить толщину h слоя меди, выделившейся за время t=5 ч при электролизе медного купороса, если плотность тока =80 А/м2.
Напряженность Н магнитного поля в центре кругового витка радиусом r=8 см равна 30 А/м. Определить напряженность H1.
Электрон движется в однородном магнитном поле с индукцией B=0,1 Тл перпендикулярно линиям индукции. Определить силу F, действующую на электрон со стороны поля, если радиус R кривизны траектории равен 0,5 см.
Вариант 2
Расстояние между двумя точечными зарядами Q1=l мкКл и Q2=–Q1 равно 10 см. Определить силу F, действующую на точечный заряд Q=0,1 мкКл, удаленный на r1=6 см от первого и на r2=8 см от второго зарядов.
Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями 1=l нКл/м2 и 2=3 нКл/м2. Определить напряженность Е поля: 1) между пластинами; 2) вне пластин. Построить график изменения напряженности вдоль линии, перпендикулярной пластинам.
Заряды Q1=1 мкКл и Q2= -1 мкКл находятся на расстоянии d=10 см. Определить напряженность Е и потенциал φ поля в точке, удаленной на расстояние r= 10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно направлению от Q1 к Q2.
Конденсатор электроемкостью С1=0,2 мкФ был заряжен, до разности потенциалов U1=320 В. После того как его соединили параллельно со вторым конденсатором, заряженным до разности потенциалов U2=450 В, напряжение U на нем изменилось до 400 В. Вычислить емкость С2 второго конденсатора.
Плоский воздушный конденсатор состоит из двух круглых пластин радиусом r= 10 см каждая. Расстояние d1 между пластинами равно 1 см. Конденсатор зарядили до разности потенциалов U =1,2 кВ и отключили от источника тока. Какую работу А нужно совершить, чтобы, удаляя пластины друг от друга, увеличить расстояние между ними до d2=3,5 см?
Л
 ампочка
и реостат, соединенные последовательно
присоединены к источнику тока. Напряжение
U на зажимах
лампочки равно 40 В, сопротивление R
реостата равно 10 Ом. Внешняя цепь
потребляет мощность Р= 120 Вт.
Найти силу тока I в
цепи.
ампочка
и реостат, соединенные последовательно
присоединены к источнику тока. Напряжение
U на зажимах
лампочки равно 40 В, сопротивление R
реостата равно 10 Ом. Внешняя цепь
потребляет мощность Р= 120 Вт.
Найти силу тока I в
цепи.Определить силу тока I3 в резисторе сопротивлением R3 (рис) и напряжение U3 на концах резистора, если ε1=4 В, ε2=3 В, R1=2 Ом, R2=6 Ом, R3=1 Ом. Внутренними сопротивлениями источников тока пренебречь.
В электролитической ванне через раствор прошел заряд Q=193 кКл. При этом на катоде выделился металл количеством вещества =1 моль. Определить валентность Z металла.
При какой силе тока I, текущего по тонкому проводящему кольцу радиусом R=0,2 м, магнитная индукция В в точке, равноудаленной от всех точек кольца на расстояние г=0,3 м, станет равной 20 мкТл?
Заряженная частица, прошедшая ускоряющую разность потенциалов U=2 кВ, движется в однородном магнитном поле с индукцией B=15,1 мТл по окружности радиусом R=l см. Определить отношение \е\/m заряда частицы к ее массе и скорость частицы.
Вариант 3
Два положительных точечных заряда Q и 4Q закреплены на расстоянии l=60 см друг от друга. Определить, в какой точке на прямой, проходящей через заряды, следует поместить третий заряд Q1 так, чтобы он находился в равновесии. Указать, какой знак должен иметь этот заряд для того, чтобы равновесие было устойчивым, если перемещения заряда возможны только вдоль прямой, проходящей через закрепленные заряды.
Тонкий стержень длиной l=12 см заряжен с линейной плотностью =200 нКл/м. Найти напряженность Е электрического поля в точке, находящейся на расстоянии r=5 см от стержня против его середины.
Вычислить потенциальную энергию П системы двух точечных зарядов Q1=100 нКл и Q2=10 нКл, находящихся на расстоянии d=10 см друг от друга.
Два конденсатора электроемкостями С1=3 мкФ и С2=6 мкФ соединены между собой и присоединены к батарее с ЭДС. ε=120 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциалов U1 и U2 между их обкладками, если конденсаторы соединены последовательно.
Конденсатор электроемкостью С1=666 пФ зарядили до разности потенциалов U =1,5 кВ и отключили от источника тока. 3атем к конденсатору присоединили параллельно второй, незаряженный конденсатор электроемкостью С2=444 пФ. Определить энергию, израсходованную на образование искры, проскочившей при соединении конденсаторов.
Даны 12 элементов с ЭДС ε= 1,5 В и внутренним сопротивлением r=0,4 Ом. Как нужно соединить эти элементы, чтобы получить от собранной из них батареи наибольшую силу тока во внешней цепи, имеющей сопротивление R=0,3 Ом? Определить максимальную силу тока Imax.
Т
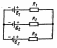 ри
источника тока с ЭДC ε1=
11 В, ε2= 4
В и ε3= 6 В и
три реостата с сопротивлениями R1=5
Ом, R2=10 Ом и R3=2
Ом соединены, как показано на рисунке.
Определить силы токов I в реостатах.
Внутреннее сопротивление источника
тока пренебрежимо мало.
ри
источника тока с ЭДC ε1=
11 В, ε2= 4
В и ε3= 6 В и
три реостата с сопротивлениями R1=5
Ом, R2=10 Ом и R3=2
Ом соединены, как показано на рисунке.
Определить силы токов I в реостатах.
Внутреннее сопротивление источника
тока пренебрежимо мало.Определить количество вещества и число атомов N двухвалентного металла, отложившегося на катоде электролитической ванны, если через раствор в течение времени t=5 мин шел ток си I=2 А.
Катушка длиной l=20 см содержит N=100 витков. По обмотке катушки идет ток 1=5 А. Диаметр d катушки равен 20 см. Определить магнитную индукцию В в точке, лежащей на оси катушки на расстоянии а=10 см от ее конца.
Протон, прошедший ускоряющую разность потенциалов U=600 В, влетел в однородное магнитное поле с индукцией B =0,3 Тл и начал двигаться по окружности. Вычислить ее радиус R..
Вариант 4
Расстояние l между свободными зарядами Q1=180 нКл и Q2=720 нКл равно 60 см. Определить точку на прямой, проходящей через заряды, в которой нужно поместить третий заряд Q3 так, чтобы система зарядов находилась в равновесии. Определить величину и знак заряда.
Прямой металлический стержень диаметром d=5 см и длиной l=4 м несет равномерно распределенный по его поверхности заряд Q=500 нКл. Определить напряженность Е поля в точке, находящейся против середины стержня на расстоянии а=1 см от его поверхности.
Какова потенциальная энергия П системы четырех одинаковых точечных зарядов Q=10 нКл, расположенных в вершинах квадрата со стороной длиной а=10 см? .
Два конденсатора электроемкостями С1=3 мкФ и С2=6 мкФ соединены между собой и присоединены к батарее с ЭДС. ε=120 В. Определить заряды Q1 и Q2 конденсаторов и разности потенциалов U1 и U2 между их обкладками, если конденсаторы соединены параллельно.
Конденсаторы электроемкостями С1=1 мкФ, С2=2 мкФ, С3=3 мкФ включены в цепь с напряжением U =1,1 кВ. Определить энергию каждого конденсатора в случае последовательного их включения.
Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС ε каждого элемента равна 1,2 В, внутреннее сопротивление r =0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R= 1,5 Ом. Найти силу тока I во внешней цепи.
Т ри источника тока с ЭДC ε1= 10 В, ε2= 6 В и ε3= 7 В и три реостата с сопротивлениями R1=5 Ом, R2=10 Ом и R3=2 Ом соединены, как показано на рисунке. Определить силы токов I в реостатах. Внутреннее сопротивление источника тока пренебрежимо мало.
Сколько атомов двухвалентного металла выделится 1 см2 поверхности электрода за время t=5 мин при плотности j=10 А/м2?
Длинный прямой соленоид из проволоки диаметром d=0,5 мм намотан так, что витки плотно прилегают друг к другу. Какова напряженность Н магнитного поля внутри соленоида при силе тока I=4 А? Толщиной изоляции пренебречь.
Электрон движется в магнитном поле с индукцией B =0,02 Тл по окружности радиусом R=1 см. Определить кинетическую энергию Т электрона (в джоулях и электрон-вольтах).
Вариант 5
Три одинаковых заряда Q=l нКл каждый расположены по вершинам равностороннего треугольника. Какой отрицательный заряд Q1 нужно поместить в центре треугольника, чтобы его притяжение уравновесило силы взаимного отталкивания зарядов?
Полусфера несет заряд, равномерно распределенный с поверхностной плотностью =1,нКл/м2. Найти напряженность Е электрического поля в геометрическом центре полусферы.
По тонкому кольцу радиусом R=10 см равномерно распределен заряд с линейной плотностью τ= 10 нКл/м. Определить потенциал φ в точке, лежащей на оси кольца, на расстоянии а=5 см от центра.
К воздушному конденсатору, заряженному до разности потенциалов U =600 в и отключенному от источника напряжения, присоединили параллельно второй незаряженный конденсатор таких же размеров и формы, но с диэлектриком (фарфор). Определить диэлектрическую проницаемость ε фарфора, если после присоединения второго конденсатора разность потенциалов уменьшилась до U1=100 В.
Конденсаторы электроемкостями С1=1 мкФ, С2=2 мкФ, С3=3 мкФ включены в цепь с напряжением U =1,1 кВ. Определить энергию каждого конденсатора в случае параллельного их включения.
К источнику тока с ЭДС ε=1,5 В присоединили катушку с сопротивлением R=0,1 Ом. Амперметр показал силу тока, равную I1=0,5 А. Когда к источнику тока присоединили последовательно еще один источник тока с такой же ЭДС, то сила тока I в той же катушке оказалась равной 0,4 А. Определить внутренние сопротивления r1 и r2 первого и второго источников тока.
О пределить силу тока I3 в резисторе сопротивлением R3 (рис) и напряжение U3 на концах резистора, если ε1=5 В, ε2=4 В, R1=2 Ом, R2=5 Ом, R3=1 Ом. Внутренними сопротивлениями источников тока пренебречь.
В медном проводнике объемом V=6 см3 при прохождении по нему постоянного тока за время t=l мин выделилось количество теплоты Q=216 Дж. Вычислить напряженность Е электрического поля в проводнике.
По прямому бесконечно длинному проводнику течет ток I=50 А. Определить магнитную индукцию В в точке, удаленной на расстояние r=5 см от проводника.
Вычислить радиус R дуги окружности, которую описывает протон в магнитном поле с индукцией В=15 мТл, если скорость протона равна 2 Мм/с.
Вариант 6
В вершинах квадрата находятся одинаковые заряды Q=0,3 нКл каждый. Какой отрицательный заряд Q1 нужно поместить в центре квадрата, чтобы сила взаимного отталкивания положительных зарядов была уравновешена силой притяжения отрицательного заряда?
Электрическое поле создано двумя точечными зарядами Q1=40 нКл и Q2= –10 нКл, находящимися на расстоянии d=10 см друг от друга. Определить напряженность Е поля в точке, удаленной от первого заряда на r1=12 см и от второго на r2=6 см.
На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью τ=10 нКл/м. Вычислить потенциал φ, создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
Электроемкость с плоского конденсатора равна 1,5 мкФ . Расстояние d между пластинами равно 5 мм. Какова будет электроемкость С конденсатора, если на нижнюю пластину положить лист эбонита толщиной d1=3 мм?
Электроемкость С плоского конденсатора равна 111 пФ. Диэлектрик - фарфор. Конденсатор зарядили до разности потенциалов U=600 В и отключили от источника напряжения. Какую работу А нужно совершить, чтобы вынуть диэлектрик из конденсатора? Трение пренебрежимо мало.
Катушка и амперметр соединены последовательно и присоединены к источнику тока. К зажимам катушки присоединен вольтметр сопротивлением RВ= 1 кOм. Показания амперметра I=0,5 А, вольтметра U=100 В. Определить сопротивление R катушки.
Т
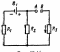 ри
сопротивления Rl=5 Ом, R2=1
Ом и R3=3 Ом, а также источник
тока с ЭДС ε1=1,4 В соединены,
как показано на рисунке определить ЭДС
ε источника тока, который надо
подключить в цепь между точками А и
В, чтобы в сопротивлении R3
шел ток силой I = 1 А в направлении,
указанном стрелкой. Сопротивлением
источника тока пренебречь.
ри
сопротивления Rl=5 Ом, R2=1
Ом и R3=3 Ом, а также источник
тока с ЭДС ε1=1,4 В соединены,
как показано на рисунке определить ЭДС
ε источника тока, который надо
подключить в цепь между точками А и
В, чтобы в сопротивлении R3
шел ток силой I = 1 А в направлении,
указанном стрелкой. Сопротивлением
источника тока пренебречь.Плотность тока j в медном проводнике равна 3 А/мм2. Найти напряженность Е электрического поля в проводнике.
Два длинных параллельных провода находятся на расстоянии r=5 см один от другого. По проводам текут в противоположных направлениях одинаковые токи I=10 А каждый. Найти напряженность H магнитного поля в точке, находящейся на расстоянии r1=2 см от одного и г2=3 см от другого провода.
Определить силу Лоренца F, действующую на электрон, влетевший со скоростью =4 Мм/с в однородное магнитное поле под углом =30° к линиям индукции. Магнитная индукция В поля равна 0,2 Тл.
Вариант 7
В элементарной теории атома водорода принимают, что электрон обращается вокруг ядра по круговой орбите. Определить скорость v электрона, если радиус орбиты r=53 пм, а также частоту n вращения электрона.
Электрическое поле создано двумя точечными зарядами Q1=10 нКл и Q2= –20 нКл, находящимися на расстоянии d=20 см друг от друга. Определить напряженность E поля в точке, удаленной от первого заряда на r1=30 см и от второго на r2=50 см.
Тонкий стержень длиной l=10 см несет равномерно распределенный заряд Q= 1 нКл. Определить потенциал τ электрического поля в точке, лежащей на оси стержня на расстоянии а=20 см от ближайшего его конца.
На пластинах плоского конденсатора равномерно распределен заряд с поверхностной плотностью σ =0,2 мкКл/м2. Расстояние d между пластинами равно 1 мм. На сколько изменится разность потенциалов на его обкладках при увеличении расстояния d между пластинами до 3 мм?
В плоский конденсатор вдвинули плитку парафина толщиной d= 1 см, которая вплотную прилегает к его пластинам. На сколько нужно увеличить расстояние между пластинами, чтобы получить прежнюю емкость?
Вычислить сопротивление R графитового проводника, изготовленного в виде прямого кругового усеченного конуса высотой h=20см и радиусами оснований, r1= 12 мм и r2=8 мм. Температура t проводника равна 20 ˚С.
Д
 ва
одинаковых источника тока с ЭДС ε=
1,2 В и внутренним сопротивлением
r=0,4 Ом соединены, как
показано на рисунке. Определить
силу тока I в цепи и разность
потенциалов U между точками А и
В в первом и втором случаях.
ва
одинаковых источника тока с ЭДС ε=
1,2 В и внутренним сопротивлением
r=0,4 Ом соединены, как
показано на рисунке. Определить
силу тока I в цепи и разность
потенциалов U между точками А и
В в первом и втором случаях.Плотность тока j в алюминиевом проводе равна 1 А/мм2. Найти среднюю скорость <v> упорядоченного движения электрон предполагая, что число свободных электронов в 1 см3 алюминия равно числу атомов.
По двум бесконечно длинным прямым параллельным проводам текут токи I=50 А и I2=100 А в противоположных направлениях. Расстояние d между проводами равно 20 см. Определить магнитную индукцию В в точке, удаленной на г1=25 см от первого и на r2=40 см от второго провода.
Квадратная проволочная рамка расположена в одной плоскости с длинным прямым проводом так, что две ее стороны параллельны проводу. По рамке и проводу текут одинаковые токи I= 1 кА. Определить силу F, действующую на рамку, если ближайшая к проводу сторона рамки находится на расстоянии, равном ее длине.
Вариант 8
Два одинаковых проводящих заряженных шара находятся на расстоянии r=60 см. Сила отталкивания F1 шаров равна 70 мкН. После того как шары привели в соприкосновение и удалили друг от друга на прежнее расстояние, сила отталкивания возросла и стала равной F2=160 мкН. Вычислить заряды Q1 и Q2, которые были на шарах до их соприкосновений. Диаметр шаров считать много меньшим расстояния между ними.
Расстояние d между двумя точечными зарядами Q1=+8 нКл и Q2= –5,3 нКл равно 40 см. Вычислить напряженность Е поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд будет положительным?
Заряд распределен равномерно по бесконечной плоскости с поверхностной плотностью σ=10 нКл/м2. Определить; разность потенциалов Δφ двух точек поля, одна из которых находится на плоскости, а другая удалена от плоскости на расстояние d=10 см.
Расстояние d между пластинами плоского конденсатора равно 1,33 мм площадь S пластин равна 20 см2. В пространстве между пластинами конденсатора находятся два слоя диэлектриков: слюды толщиной d1=0,7 мм и эбонита толщиной d2=0,3 мм. Определить электроемкость с конденсатора.
Вычислить энергию W электростатического поля металлического шара, которому сообщен заряд Q=100 нКл, если диаметр d шара равен 20 см.
Определить плотность тока j в железном проводнике длиной, l = 10 м, если провод находится под напряжением U =6 В.
Два элемента (ε1=1,2 В, r1=0,1 Ом; ε2=0,9 В, r2=0,3 Ом) соединены одноименными полюсами. Сопротивление R соединительных проводов равно 0,2 Ом. Определить силу тока I в цепи.
Сила тока I в металлическом проводнике равна 0,8 А, сечение S проводника 4 мм2. Принимая, что в каждом кубическом сантиметре металла содержится n=2,5 .1022 свободных электронов определить среднюю скорость их упорядоченного движения.
По двум бесконечно длинным прямым параллельным проводам текут токи I1=20 А и I2=30 А в одном направлении. Расстояние d между проводами равно 10 см. Вычислить магнитную индукцию В в точке, удаленной от обоих проводов на одинаковое расстояние г=10 см.
Прямой провод длиной l=10 см, по которому течет ток I=20 А, находится в однородном магнитном поле с индукцией В =0,01 Тл. Найти угол α между направлениями вектора В и тока, если на провод действует сила F=10 мН.
Вариант 9
Два одинаковых проводящих заряженных шара находятся на расстоянии r=30 см. Сила притяжения F1 шаров равна 90 мкН. После того как шары были приведены в соприкосновение и удалены друг от друга на прежнее расстояние, они стали отталкиваться с силой F2=160 мкН. Определить заряды Q1 и Q2, которые были на шарах до их соприкосновения. Диаметр шаров считать много меньшим расстояния между ними.
Определить напряженность Е электрического поля, создаваемого точечным зарядом Q=10 нКл на расстоянии r=10 см от него. Диэлектрик — масло.
Две круглые металлические пластины радиусом R=10 см каждая, заряженные разноименно, расположены одна против другой параллельно друг другу и притягиваются с силой F=2мН. Расстояние d между пластинами 1 см. Определить разность потенциалов между пластинами.
Между пластинами плоского конденсатора, заряженного до разности потенциалов U =600 В, находятся два слоя диэлектриков: стекла толщиной d1=7 мм и эбонита толщиной d2=3 мм. Площадь S каждой пластины конденсатора равна 200 см2. Найти: 1) электроемкость С конденсатора; 2) смещение D, напряженность Е поля и падение потенциала Δφ в каждом слое.
Электрическое поле создано заряженной (Q=0,1 мкКл) сферой радиусом R=10 см. Какова энергия W поля, заключенная в объеме, ограниченном сферой и концентрической с ней сферической поверхностью, радиус которой в два раза больше радиуса сферы?
Сила тока в проводнике равномерно нарастает от I0=0 до I=3 А в течение времени t=10c. Определить заряд Q, прошедший в проводнике.
Имеется N одинаковых гальванических элементов с ЭДС ε и внутренним сопротивлением ri каждый. Из этих элементов требуется собрать батарею, состоящую из нескольких параллельно соединенных групп, содержащих по n последовательно соединенных элементов. При каком значении n сила тока I во внешней цепи, имеющей сопротивление R, будет максимальной? Чему будет равно внутреннее сопротивление Ri батареи при этом значении п?
Пространство между пластинами плоского конденсатора имеет объем V =375 см3 и заполнено водородом, который частично ионизирован. Площадь пластин конденсатора S=250 см2. При каком напряжении U между пластинами конденсатора сила тока I, протекающего через конденсатор, достигнет значения 2 мкА, если концентрация n ионов обоих знаков в газе равна 5,3*107 см-3? Принять подвижность ионов b+=5,4*10-4 м2/(В*с), b-=7,4*10-4 м2/ (В*с).
По контуру в виде равностороннего треугольника идет ток I=40 А. Длина а стороны треугольника равна 30 см. Определить магнитную индукцию В в точке пересечения высот.
Прямой провод, по которому течет ток 1=1 кА, расположен в однородном магнитном поле перпендикулярно линиям индукции. С какой силой F действует поле на отрезок провода длиной l=1 м если магнитная индукция В равна 1 Тл?
ТАБЛИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН




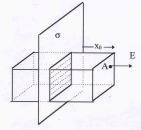

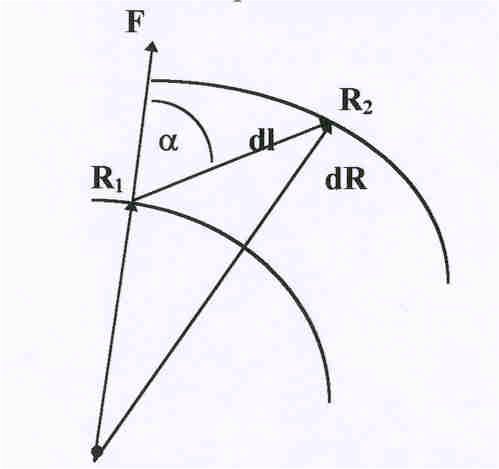 Рис.8. К расчету
элементарной работы.
Рис.8. К расчету
элементарной работы.
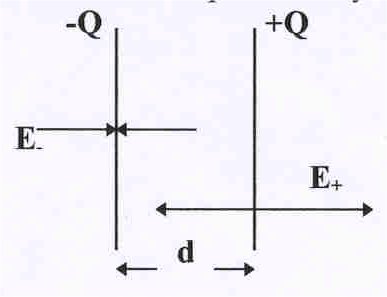

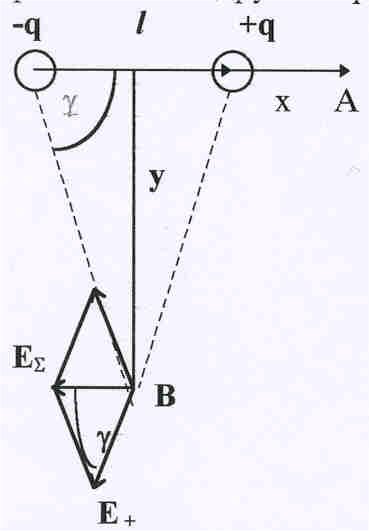
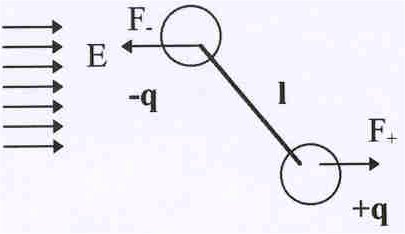




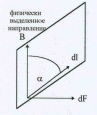

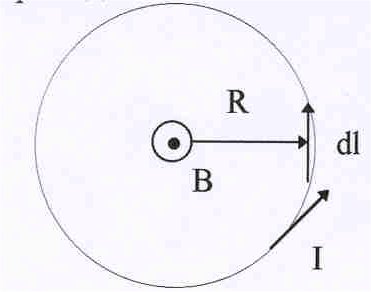
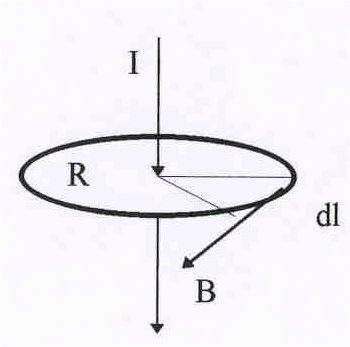

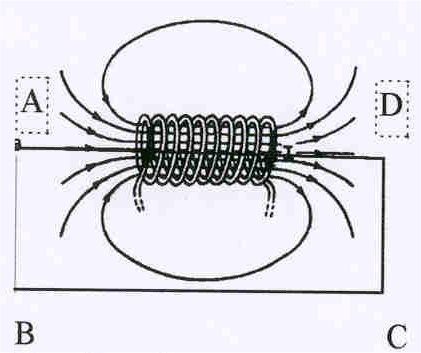

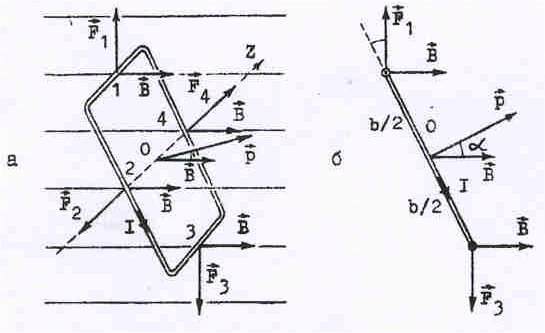
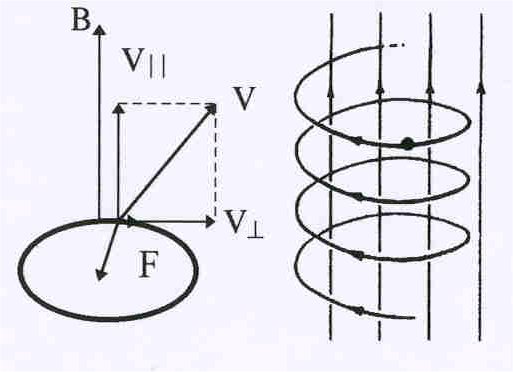
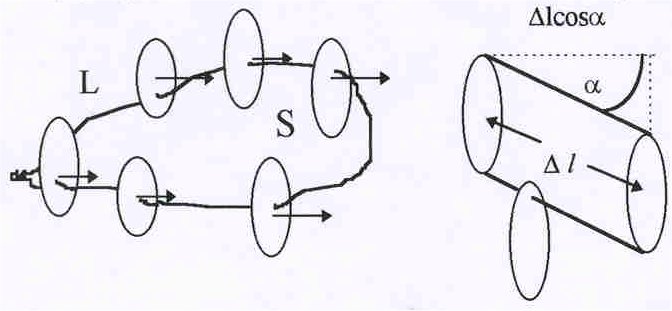


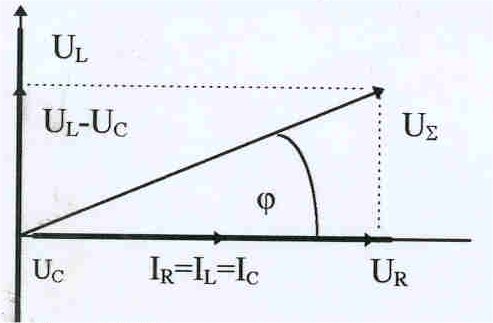

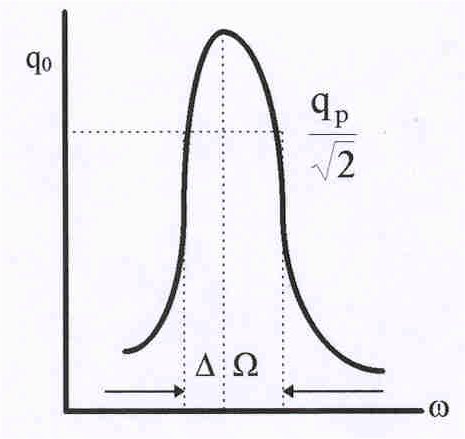
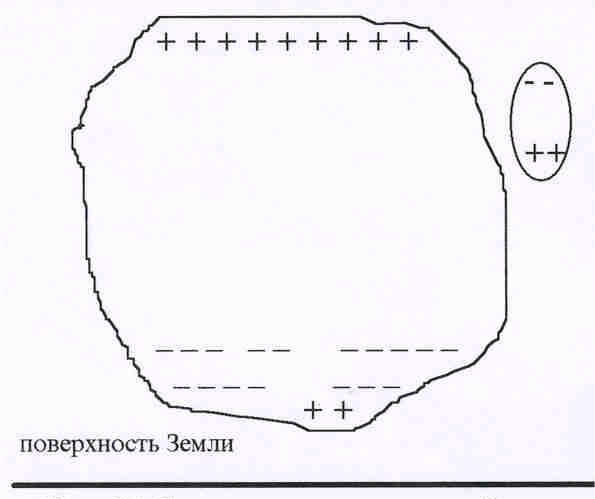
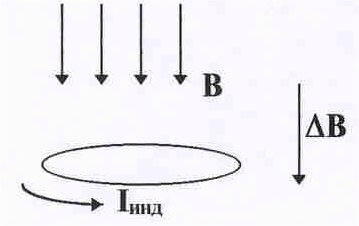

 Рис.36.
К вычислению циркуляций для векторов
Е и В.
Рис.36.
К вычислению циркуляций для векторов
Е и В.