2.3. Планы ускорений

Последовательность построения плана ускорений также определяется

формулой строения механизма: сначала строим план для кривошипа 2, затем

для группы Ассура (3,4) и, наконец, для группы (5,6).

У кривошипа 2 полное ускорение a_A точки А равно геометрической сумме двух составляющих: нормального ускорения , направленного к центру вращения, то есть от точки А к точке О, и тангенциального , на-

правленного перпендикулярно OA в сторону, соответствующую направле-

нию углового ускорения ε₂. Следовательно,

a̅_{A =} +

a_A = * l_OA = 12² * 0.12 = 17.28(м/с²)

Так как принято, что ω₂ =const. Следовательно, тангенциальное

ускорение =0.

Ускорение изобразим отрезком па равное 100 мм.

µ_a = = = 0,173

Ускорение точки В определяется совместным решением системы век-

торных уравнений.

a̅_B = a̅_A + a̅_BA = a̅_O + +

= * l_BA =5.45²* 0,264= 7.84м/с²

Нормальная составляющая направлена по положению шатуна АВ от

точки В к точке А.

– касательная составляющая направлена перпендикулярно шатуну АВ

На плане ускорений из конца вектора a̅_A проводится линия действия

на которой в направлении от точки В к точке А откладывается отрезок:

a̅n̅₃ = = =45.32мм.

Через конец вектора проводится линия действия , перпендику-лярно этому вектору.

Аналогичным образом получим a_B относительно точки О.

a̅_B = a̅_O + +

= * l_BD = 3.39² * 0.230 = 2.64 м/с²

n₄= = = 15.26 мм.

Определяем ускорение точки E a_E :

a̅_D = a̅_B + +

= * l_EC = 1.20² * 0,432 = 0.62 м/с²

n₅= = = 3.58 мм.

Умножая векторы ускорений на масштаб, получим их численные значения:

a_a = πa * = 100 * 0,173 = 17.3 м/с²

a_b = πb * = 42 * 0.173 = 7.27 м/с²

a_d= ad * = 21 * 0,173 = 3.63 м/с²

a_BA = ab * = 50 * 0,173 = 8.65

a_DB = bd * = 18 * 0.173 = 3.11

= πS₃ * = 71 * 0,173 = 12.28 м/с²

= πS₄ * = 21 * 0,173 = 3.63 м/с²

= πS₅ * = 31 * 0,173 = 5.36 м/с²

= πS₆ * =26 * 0,173 = 4.50 м/с²

Определяем угловые ускорения шатунов рад/с²:

ε₃ = = = 20.31 рад/с

ε₄ = = = 30.09 рад/с²

ε₅ = = = 10.41 рад/с²

Рис 3. План ускорений

3. Силовой анализ

Динамический анализ механизма состоит в определении реакции в ки-

нематических парах и уравновешивающих сил, обеспечивающий заданный

закон движения механизма. Динамический анализ плоских механизмов

обычно производится кинетостатическим методом.

По этому методу механизм раскладывается на структурные группы

(группы Ассура и ведущее звено). Прикладываем к ним задаваемые силы

(силы полезного сопротивления или движущие силы) и искомые реакции в

кинематических парах. Составляем и решаем уравнения статики.

Динамический анализ ведется от последней группы Ассура к ведущему

звену, для которого определяются кроме реакции стойки и уравновешиваю-

щая сила.

Определяем силы тяжести звеньев:

G₃ = m₃ * g = 10.4 *10 = 104 H

G₄ = m₄ * g = 8.6 * 10 = 86 H

G₅ = m₅ * g = 10.8 * 10 =108 H

G₆ = m₆ * g = 18 * 10 = 180 H

Направление силы тяжести вертикально вниз. Точки приложения цен-

тра масс звеньев

Определяем силы и моменты инерции звеньев:

P_u3 = −a_S3 * m₃ = −12.28 * 10.4 = −131.76 H

P_u4 = −a_S4 * m₄ = −3.46 * 8.64 = −29.89 H

P_u5 = −a_S5 * m₅ = −5.54 * 10.8 = −59.83 H

P_u6 = −a_S6 * m₆ = −3.46 * 18 = -62.28 H

=

I_S3= − =0.072

I_S4= =0.046

I_S5= =0.20

M_u3 = −I_S3 * ε₃ =  0.072 * 20.31 = 1.46 Н м;

M_u4 = −I_S4 * ε₄=  0.046 * 30.09 =1.38 Н м;

M_u5 = −I_S5 * ε₅ = −0.20 * 10.41 =- 2.08 Н м;

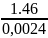= = = 608.33 Н мм;

= = = 576.71 Н мм;

= = = 866.67 Н мм.

Векторы P_u3, P_u4 и P_u5 противоположно направлены a̅_S3, a̅_S4 и a̅_S5,

приложены в точках приложения центр масс S₃, S₄ и S₅. Моменты , и противоположно направлены ε₃, ε₄ и ε₅.