2.6 Контрольні питання

1. Основна характеристика режиму холостого ходу лінії передачі електричного струму.

2. Основна характеристика режиму короткого замикання лінії передачі електричного струму.

3. Основна характеристика робочого режиму лінії передачі електричного струму.

4. За яких умов досягається максимальний К.К.Д. лінії передачі?

5. При яких значеннях величини опору навантаження потужність на опорі навантаження максимальна?

6. який з режимів роботи ліннії вважається аварійним і чому?

Лабораторна робота №3 ДОСЛІДЖЕННЯ ЛАНЦЮГІВ, ЩО МІСТЯТЬ РЕАКТИВНІ ЕЛЕМЕНТИ

3.1. Мета роботи: Дослідження ланцюгів, що містять реактивні елементи, у колах з синусоїдальними та імпульсними сигналами.

3.2 Зміст роботи:

Для даного електричного ланцюга (рис.3.1):

- встановити необхідні параметри ланцюга;

- провести дослідження характеристик електричного ланцюга, що містить реактивні елементи, відповідно до порядку виконання роботи;

- побудувати необхідні осцилограми струмів і напруг, провести розрахунок вказаних величин;

- зробити висновки за результатами роботи.

3.3 Теоретичні відомості

Ланцюг з реальною котушкою індуктивності

Реальна котушка індуктивності відрізняється від ідеальної тим, що змінний струм у ній супроводжується не тільки зміною енергії в магнітному полі, але і перетворенням електричної енергії в інший вигляд. Зокрема, у дроті котушки електрична енергія перетвориться в теплову у відповідності із законом Ленца-Джоуля.

У ланцюзі змінного струму процес перетворення електричної енергії в інший вигляд характеризується активною потужністю ланцюга Р, а зміна енергії в магнітному полі – реактивною потужністю Q; отже, у реальній котушці активна і реактивна потужності відмінні від нуля. Тому в схемі заміщення реальна котушка повинна бути представлена активним і реактивним елементами.

Виділення у реальній котушці двох елементів є штучним, оскільки конструктивно обидва елементи нероздільні; проте такою ж схемою заміщення можна представити реальний ланцюг із двох конструктивно не суміщених елементів, один з яких характеризується тільки активною потужністю P (при Q=0), а інший – реактивною (індуктивною) потужністю Q (при P=0).

Схема заміщення котушки з послідовним з'єднанням елементів

У схемі з послідовним з'єднанням елементів реальна котушка характеризується активним опором R і індуктивністю L.

Активний опір визначається величиною потужності втрат

R=Р/I²,

а індуктивність – конструкцією котушки.

Припустимо, що струм в котушці (рис.3.1,а) виражається рівнянням i = I_msin t.

При проходженні змінного струмі у котушці виникає Е.Р.С. самоіндукції е_L, тому струм залежить від дії прикладеної напруги і е_L. Рівняння електричної рівноваги ланцюга, складене за другим законом Кірхгофа, має вигляд

u + e_L = iR,

або .

а) б)

Рисунок 3.1 – Схема заміщення реальної котушки індуктивності (ланцюг R, L)

Прикладена до котушки напруга складається з двох доданків, один з яких (u_R) - падіння напруги у активному опорі, а інший ( ) врівноважує Е.Р.С. самоіндукції. Відповідно до цього котушку в схемі заміщення можна представити активним і індуктивним опорами, сполученими послідовно (рис.3.1,б).

Додатково відмітимо, що обидва доданки у правій частині рівності (3.1) є синусоїдальними функціями часу: u_R співпадає по фазі із струмом, а u_L випереджає струм на 90°. Тому

.

Векторна діаграма напруг

Вектор загальної напруги для ланцюга, приведеного на рис. 3.1б:

U = U_R + U_L.

Для побудови векторної діаграми (рис.3.2,а) заздалегідь вибираємо масштаби струму M_i і напруги М_u.

За початковий вектор діаграми приймаємо вектор струму I. Напрям цього вектора співпадає з позитивним напрямом осі, від якої відлічуються фазові кути (початкова фаза заданого струму ). Вектор U_R по напряму співпадає з вектором струму I, а вектор U_L направлений перпендикулярно вектору I з позитивним кутом.

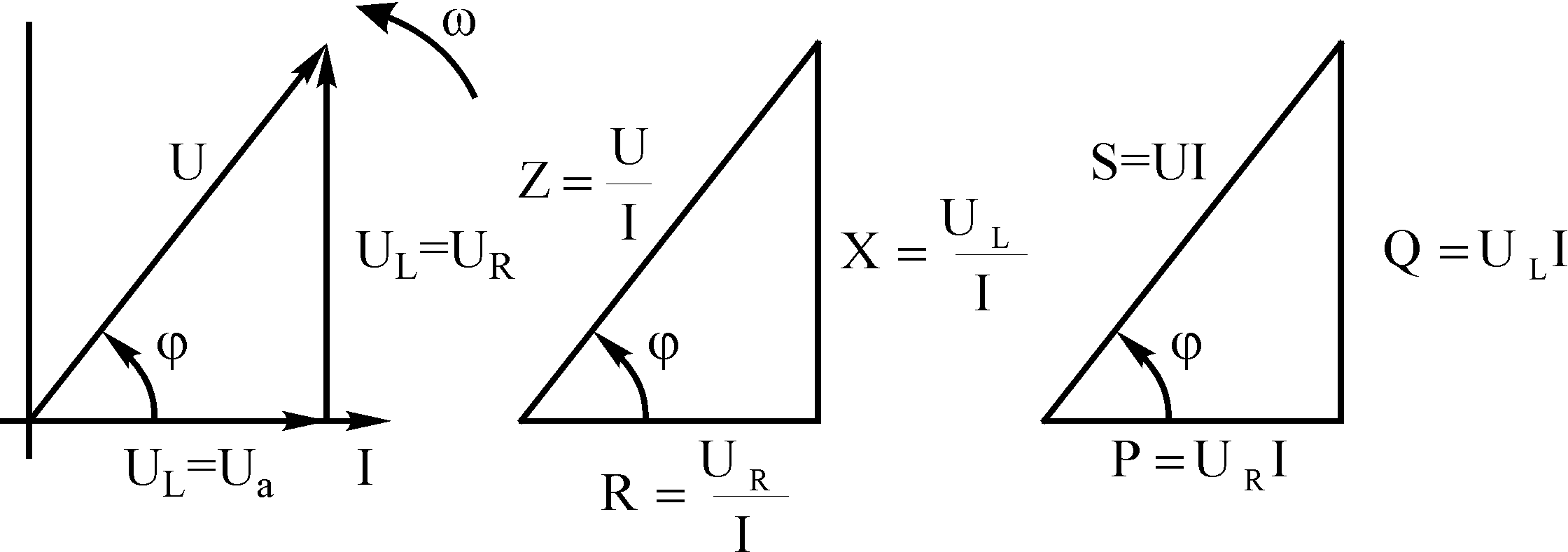
а) б) в)

Рисунок 3.2 – Векторна діаграма ланцюга, трикутники опорів і потужностей

З діаграми видно, що вектор загальної напруги за величиною дорівнює гіпотенузі прямокутного трикутника, катетами якого є вектори падінь напруги в активному і індуктивному опорах U_R і U_L

,

а за напрямком U випереджає вектор струму I на кут  , причому 90° >  > 0,

Проекція вектора напруги U на напрям вектора струму називається активною складовою вектора напруги і позначається U_a; для даної схеми U_a = U_R.

Проекція вектора напруги U на напрям, перпендикулярний вектору струму, називається реактивною складовою вектора напруги і позначається U_p. для даної схеми U_p = U_L.

Аналогічно діаграмі напруг, можна зобразити трикутник опорів (рис.3.2,б), одним з катетів якого є активний опір R=U_R/I , другим - індуктивний опір X_L = U_L/I , а гіпотенузою - величина повного опору Z=U/I (як відношення діючої напруги до діючого струму ланцюга. З трикутника опорів виходить

.

Величина повного опору Z входить як коефіцієнт до співвідношення між діючими величинами напруги і струму (за законом Ома):

,

звідки визначаються співвідношення для кута  між сторонами трикутника:

cos  = U_R/U = R/Z,.. sin = U_L/U = X_L/Z, .tg  = U_L/U = X_L/R.

Потужність котушки

Миттєва потужність котушки

p = ui = U_msin(t + )I_msin t.

Із графіка миттєвої потужності (рис.3.3) видно, що протягом періоду потужність чотири рази зміняє знак; отже, змінюється і напрям потоку енергії .

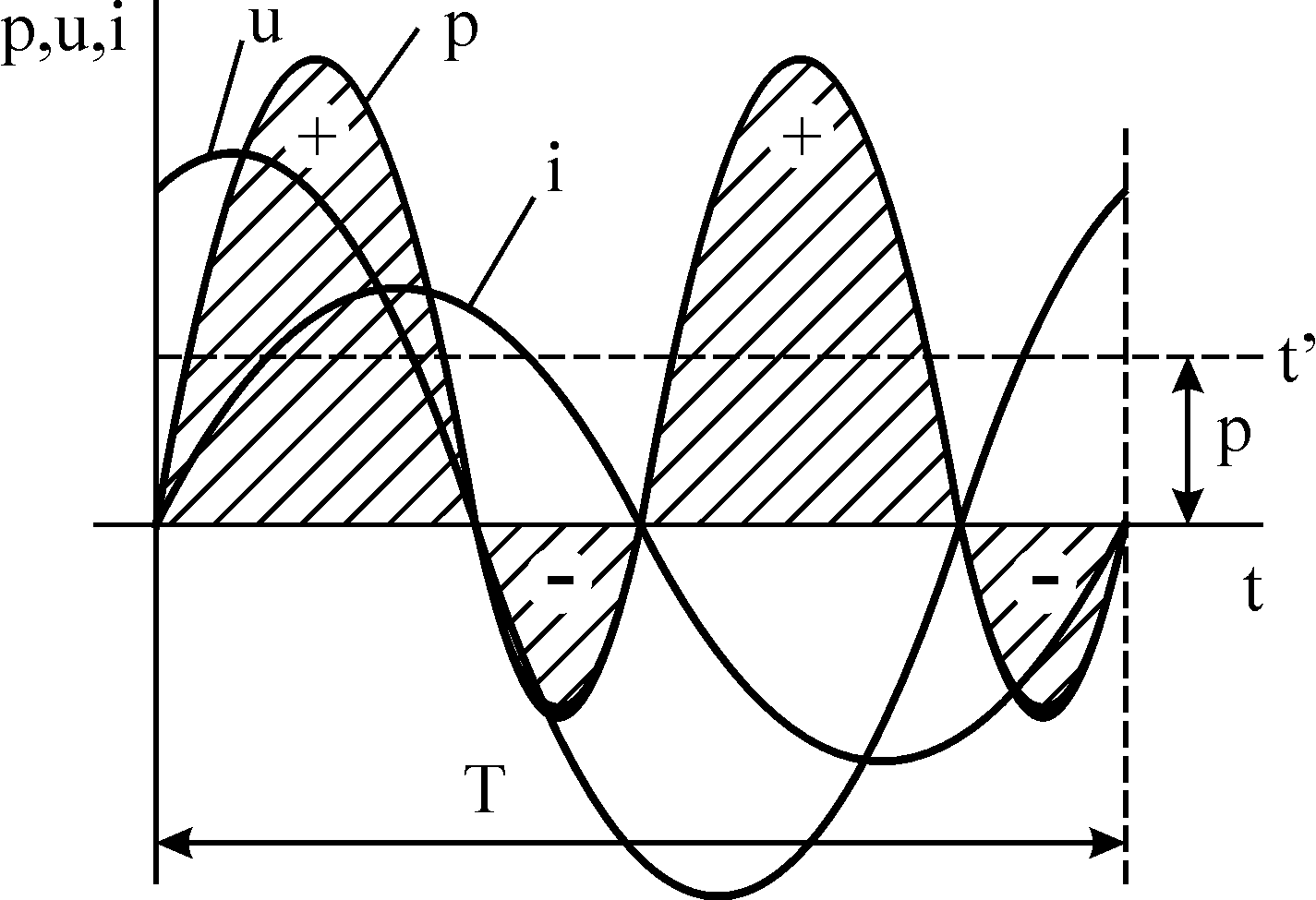
Рисунок 3.3 – Графік миттєвої потужності ланцюга

При позитивному значенні потужності енергія переходить від джерела в приймач, а при негативному – навпаки; кількість енергії, що поступила в приймач (позитивна площа) при цьому більше поверненої назад (негативна площа).

Отже, в ланцюзі з активним опором і індуктивністю частина енергії, що поступає від генератора, необоротно перетворюється на інший вид енергії. Швидкість необоротного процесу перетворення енергії оцінюється середньою (активною) потужністю Р, швидкість обмінного процесу характеризується реактивною потужністю Q.

Для активного опору Р  = U_RI; Q = 0; для індуктивного - Р = 0; Q = U_LI.

Співвідношення між повною потужністю та її складовими аналогічні таким для опорів (рис.3.2,в):

S=UI=I²Z; , P=UIcos j; Q=UIsin j.

Відношення активної потужності ланцюга до її повної потужності називають коефіцієнтом потужності cos  = P/S.

Як правило, коливання енергії в ланцюзі не тільки даремні, але і шкідливі, оскільки при цьому в приймачі не здійснюється повного перетворення електричної енергії в роботу або тепло, а усполучних дротах вона втрачається.

Ланцюг з реальним конденсатором

При змінній напрузі на реальному конденсаторі окрім струму зсуву є невеликі струми провідності через товщу діелектрика (об'ємний струм) і уздовж поверхні (поверхневий струм), які супроводжуються втратами енергії. Разом із зміною енергії електричного поля, що характеризується реактивною потужністю Q йде необоротний процес перетворення електричної енергії в теплову, швидкість якого виражається активною потужністю Р.

Тому в схемі заміщення реальний конденсатор повинен бути представлений активним і реактивним елементами; останнє - це розрахунковий прийом, оскільки конструктивно елементи виділити не можна.

Схема заміщення конденсатора з паралельним з'єднанням елементів

Реальний конденсатор (із втратами) можна представити еквівалентною схемою паралельного з'єднання активної G і ємнісної В_с провідності (рис.3.4), причому активна провідність визначається потужністю втрат в конденсаторі , а ємність – конструкцією конденсатора.

Рисунок 3.4 – Схема заміщення реального конденсатора

При такому зєднанні гілок, згідно першого закону Кірхгофа, загальний струм i рівний сумі струмів у гілках з активною і ємнісною провідностями:

i = i_G + i_C .

Враховуючи, що струм i_G співпадає по фазі з напругою, а струм i_C випереджає напругу на чверть періоду, рівняння загального струму можна записати в наступному вигляді:

i = I_Gm sint + I_Cm sin(t+/2),

де I_Gm = GU_m, a I_Cm = B_CU_m

Векторна діаграма струмів

Діючі величини загального струму I та його складових визначаються методом векторного складання за рівняннями I = I_G + I_C ; I_G = GU; I_C = B_CU.

Першим на векторній діаграмі зображається вектор напруги U (рис.3.5,а), напрям якого вибирають співпадаючим з позитивним напрямом осі абсцис, від якої відлічуються фазові кути (початкова фаза напруги _u = 0). Вектор I_G співпадає по напряму з вектором U, а вектор I_C направлений перпендикулярно вектору U з позитивним кутом.

З векторної діаграми видно, що вектор загальної напруги відстає від вектора загального струму на кут , причому 90° >  > 0.

Вектор I є гіпотенузою прямокутного трикутника, катети якого – складові вектори I_G і I_C:

I_G = I cos ; I_C = Isin ;

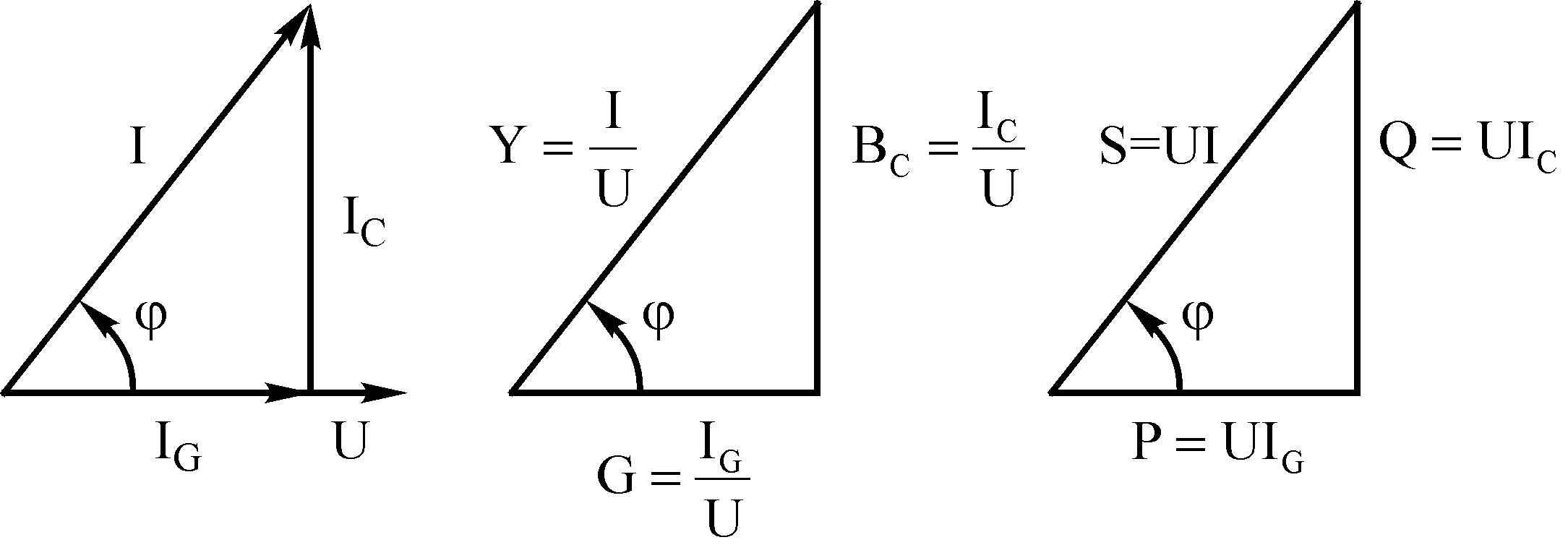
а) б) в)

Рисунок 3.5 – Трикутники струмів, провідностей, потужностей

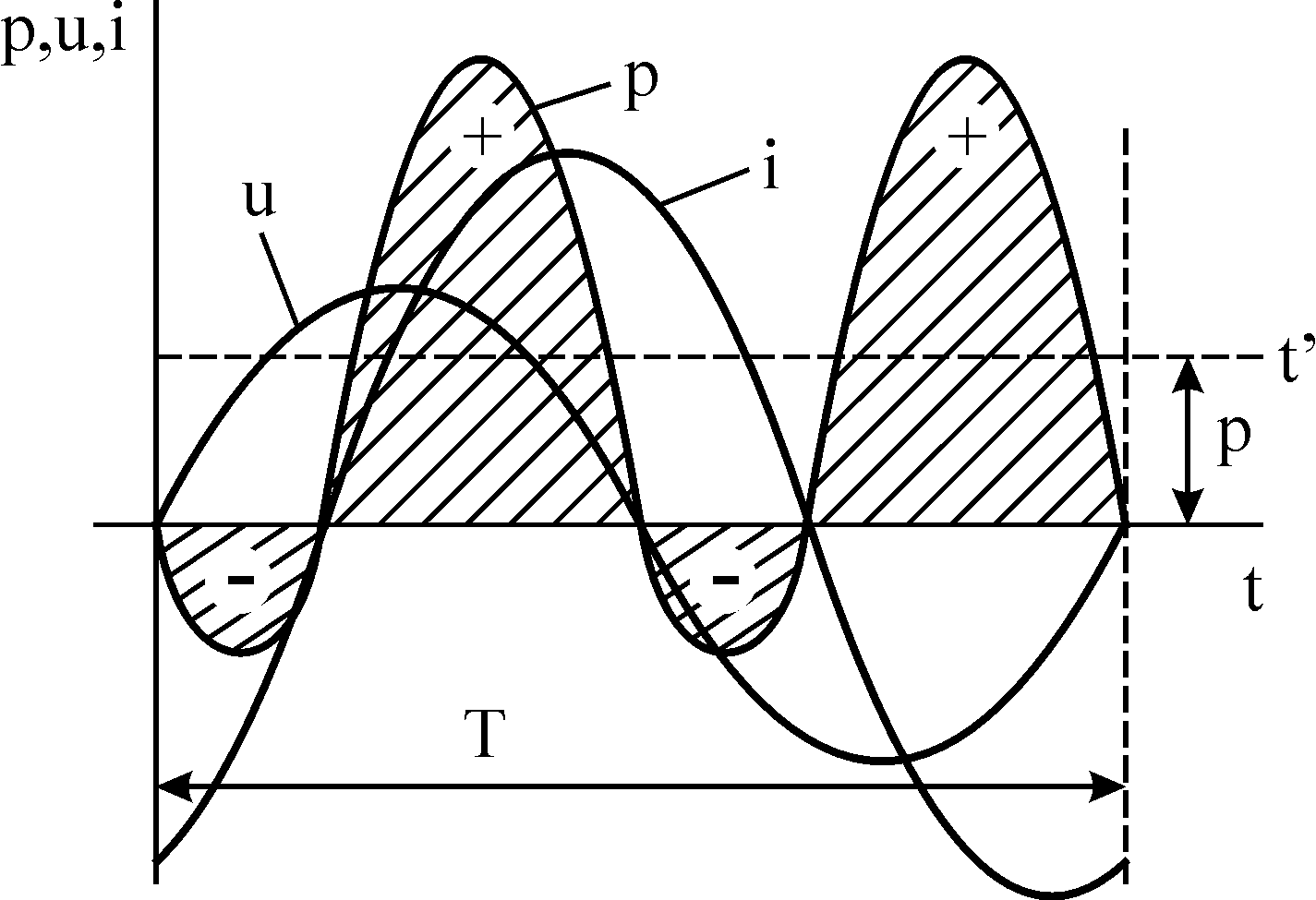
Рисунок 3.6 – Графік миттєвої потужності ланцюга

Трикутник провідностей

Аналогічно діаграмі струмів, можна зобразити трикутник провідностів (рис.3.5,б), одним з катетів якого є активна провідність G = I_G/U, другим - індуктивна провідність В_с = I_C/U, а гіпотенузою – повна провідність ланцюга Y = I/U:

Зв'язок між діючими величинами напруги і струму та коефіцієнтом потужності виражається співвідношеннями:

; U = I/Y;

Потужність

Вираз миттєвої потужності реального конденсатора

співпадає з виразом миттєвої потужності котушки; аналогічними формулами визначаються і величини активної, реактивної і повної потужностей.

Схема заміщення конденсатора з послідовним з'єднанням елементів

Реальний конденсатор, так само як і котушка, на розрахунковій схемі може бути представлений послідовним з'єднанням двох ділянок: з активним (R) і ємнісним (Х)_с опорами.

Рисунок 3.7 – Варіанти схеми заміщення реального конденсатора

На рис.3.7,а така схема показана порівняно з схемою паралельного з'єднання активної і ємнісної провідностей (рис.3.7,6). Всі висновки і формули, одержані для прикладу схеми із котушкою індуктивності, будуть справедливими і для прикладу конденсатора (за умови заміни індуктивного опору ємнісним опором).

Конденсатори, вживані на практиці, мають відносно малі втрати енергії; тому в схемах заміщення вони представлені найчастіше тільки реактивною частиною, тобто ємністю .

Перехідні процеси

Перехідні процеси виникають унаслідок зміни Е.Р.С. в ланцюзі чи напруги, прикладеної до ланцюга, або у зв'язку зі зміною параметрів ланцюга. Безпосередніми причинами виникнення перехідних процесів можуть бути комутаційні зміни режимів (включення або виключення) джерел живлення і приймачів енергії, короткі замикання на ділянках електричних ланцюгів, зміни механічного навантаження електродвигунів і т. ін.

Електромагнітні процеси, що відбуваються в електричних ланцюгах при переході від одного сталого режиму до іншого, називають перехідними процесами, а струми (напруги) в ланцюзі під час перехідного процесу – відповідно, перехідними струмами (напругами).

Тривалість перехідних процесів в електричних ланцюгах найчастіше складає десяті і соті долі секунди. Проте знання характеру їх дуже важливо, оскільки і за такий малий час можливі різкі збільшення струмів і напруг, які можуть виявитися небезпечними для електричних установок.

Співвідношення тривалості сталих і перехідних режимів може бути самим різним і залежить від умов експлуатації і призначення електричних ланцюгів. Одні з них практично весь час працюють в сталому режимі (двигуни з тривалим незмінним навантаженням, лампи електричного освітлення), інші, навпаки, безперервно знаходяться у перехідному режимі (двигуни з повторно-короткочасним навантаженням, лінії зв'язку під час передачі інформації, імпульсні пристрої автоматики, рахунково-вирішальні машини в період роботи).

Перший закон комутації застосовується до ланцюгів, що містять котушку індуктивності: i (t = - 0) = i (t = + 0),

тобто, струм в котушці індуктивності не може змінитися стрибком; миттєвий струм в гілці з індуктивністю в перший момент перехідного періоду (при t = + 0) залишається таким же, яким він був в останню мить попереднього сталого режиму (при t = - 0).

Так, електричний стан ланцюга що містить котушку індуктивності (рис.3.8) у будь-який момент перехідного періоду характеризується рівнянням

U = U _R  + U _L = iR + L(di/dt),

яке виражає баланс напруг в ланцюзі; звідси:

.

Дане диференційне рівняння характеризує закон зміни струму в котушці після замикання рубильника у схемі рис.3.8. Так, при підключення котушки індуктивності до джерела постійної напруги струм у ланцюзі збільшується, але не миттєво; відповідний графік перехідного струму приведено на рис. 3.9.

Рисунок 3.8 – До першого закону комутації

Рисунок 3.9 – Графік перехідного струму після включення ланцюга на постійну напругу

Якщо припустити, що за наявності в ланцюзі опору R струм змінювався б по лінійному закону з найбільшою швидкістю (пряма i_L), то сталої величини I він досяг би за найменший час t = τ. Цей проміжок часу є важливою характеристикою і називається постійною часу електричного ланцюга.

Постійну часу можна визначити графічно (рис.3.10), якщо провести дотичну Оа до кривої струму на початку координат і крапку а перетину дотичної з асимптотою спроектувати на вісь часу. Відрізок Оа' в масштабі часу і виразить постійну часу. Таку ж довжину має відрізок а'b', який можна одержати, якщо провести дотичну до кривої струму в будь-якій точці а₁, знайти точку b перетину дотичної з асимптотою і спроектувати точки а₁ і b на вісь часу.

Аналітичний вираз постійної часу:

τ = L/R,

тобто постійна часу визначається лише параметрами R і L даного ланцюга.

Вимушена і вільна складові перехідного струму

Перехідний струм можна розглядати як алгебраїчну суму двох складових:

.

Перша складова є струмом, сталим в ланцюзі після закінчення перехідного процесу (пряма i _пр на рис.3.10). Цей струм визначається безперервною дією постійної напруги U в перехідному і сталому режимах. Його називають вимушеним струмом.

Друга складова виникає на початку перехідного процесу і поступово затухає до нуля, після чого перехідний процес вважається закінченим (крива i_CB на рис.3.10). Ця складова перехідного струму називається вільним струмом.

Із рівняння для вільної складової перехідного струму

і _в = Ie^-t/τ

виходить, що постійна часу електричного ланцюга рівна інтервалу часу, протягом якого вільний струм в цьому ланцюзі убуває в е раз.

Вплив величини напруги і параметрів ланцюга на перехідний процес

Перехідний процес при включенні ланцюга з R і L на постійну напругу U характеризують три показники: сталий струм, початкова швидкість зміни струму і постійна часу ланцюга; при цьому сталий струм і початкова швидкість зміни струму залежать від напруги, а постійна часу ланцюга, що характеризує тривалість перехідного процесу, від напруги не залежить (рис.3.11).

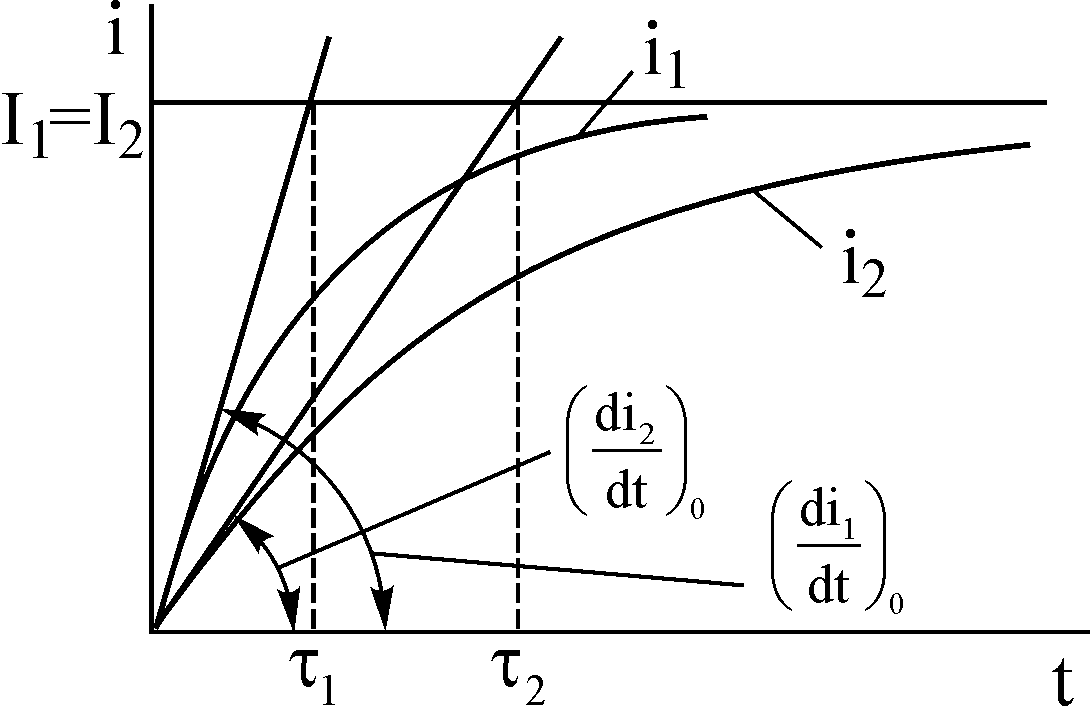
а) б) в)

Рисунок 3.11 – Графіки перехідного струму при різних напругах на затисках ланцюга (а), різних опорах (б) і індуктивностях (в) ланцюга

Відключення котушки індуктивності від джерела постійної напруги

Відключення приймачів електричної енергії від джерела або від мережі здійснюється розривом ланцюга в одній або декількох крапках. Зустрічаються випадки, коли елементи ланцюга, що мають велику індуктивність, при розриві ланцюга одночасно замикаються накоротко або на розрядний опір.

При розмиканні електричного ланцюга з котушкою індуктивності (рис.3.14,а) у момент розриву ланцюга напруга між контактами вимикача В, що розходяться, різко збільшується від нуля до U+ U _L. Швидкість зміни струму у момент розриву ланцюга , тому величина може бути досить великою. Повітряний проміжок між контактами пробивається і утворюється іскра, за рахунок чого струм в ланцюзі зберігається якийсь час після початку розриву контактів.

При великій потужності джерела іскровий розряд може перейти у дуговий; для гасіння електричної дуги вимикаючі апарати, як правило, забезпечуються дугогасильними пристосуваннями.

Рисунок 3.14 – Схеми розмикання ланцюга з індуктивністю

В деяких випадках (наприклад, при виключенні обмоток збудження електричних машин) напруга може досягати величин, небезпечних для ізоляції. Значного підвищення напруги можна уникнути, якщо одночасно з відключенням індуктивної котушки від джерела замкнути її на розрядний опір (рис.3.14,б).

Перехідний процес в замкнутому контурі «котушка–розрядний опір» відрізняється від процесу в ланцюзі рис.3.14,а тим, що швидкість зміни струму залежить від параметрів ланцюга R і L.

Після відключення ланцюга від джерела енергії (рис.3.14,б) в короткозамкнутому контурі, що утворився, струм не може зменшитися миттєво до нуля, а підтримується протягом перехідного періоду, поки енергія магнітного поля котушки не зменшиться до нуля (в активному опорі ланцюга R при цьому здійснюється необоротний процес перетворення електричної енергії у теплову).

Зміна опору в ланцюзі з індуктивністю

При включенні котушки індуктивності, що має параметри R і L, опір ланцюга зменшується стрибком від ∞ до R, а при виключенні воно збільшується від R до ∞. Відповідно до таких змін опору струм в ланцюзі за час перехідного періоду збільшується від 0 до I або зменшується від I до 0.

При стрибкоподібній зміні опору ланцюга в кінцевих межах теж виникає перехідний процес, який у загальних рисах подібний вже розглянутим процесам.

Другий закон комутації застосовується до ланцюгів, що містять ємність:

u (t = - 0) =u (t = + 0),

тобто, напруга на ємності не може змінитися стрибком; напруга на ємності в перший момент перехідного періоду (при t = + 0) залишається такою, яким вона була в останню мить попереднього сталого режиму(при t = - 0).

Електричний стан ланцюга (рис.3.11) у будь-який момент перехідного періоду характеризується рівнянням, складеним за другим законом Кірхгофа:

U = U _с + U _R = u_c + iR = U _с + i C(du_c/dt).

Рисунок 3.11 – До другого закону комутації

Зарядка конденсатора

Аналіз процесу зарядки конденсатора від джерела постійної напруги багато в чому співпадає з аналізом перехідного процесу після включення котушки на постійну напругу, оскільки рівняння електричного стану є аналогічними.

Графіки залежності напруги на конденсаторі u_C і зарядного струму i_з від часу зображені на рис.3.12.

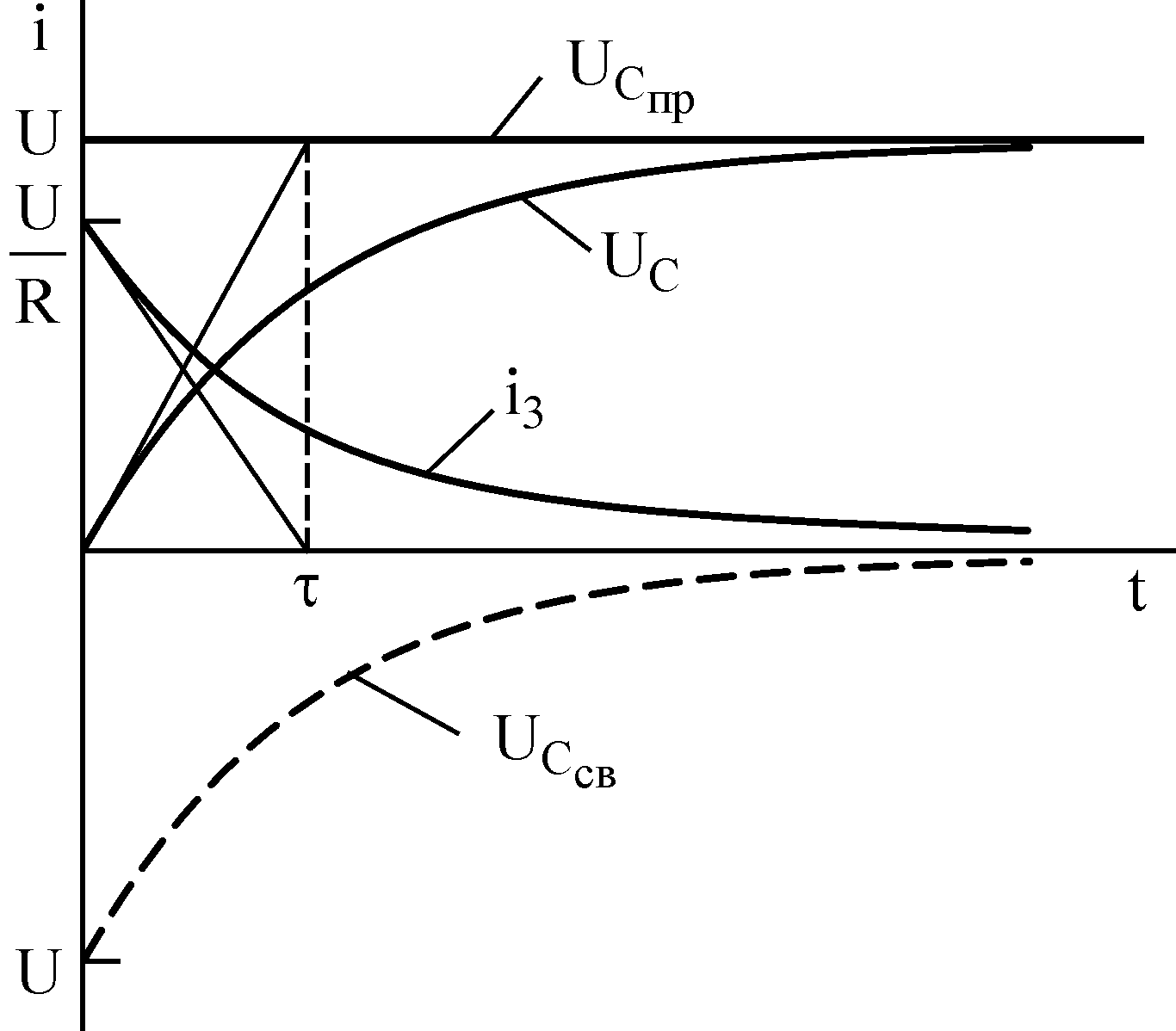
Рисунок 3.12 – Графіки перехідних струмів і напруг при зарядці конденсатора

Постійна часу ланцюга (τ = RC) є показником тривалості перехідного процесу і залежить від параметрів ланцюга R і С.

Конденсатор знаходиться під дією вимушеної і вільної складових напруги

u_С = u_{С пр} + u_{С cв} = U + ,

а зарядний струм складається тільки з вільної складової

,

оскільки а вимушена складова відсутня: i_пр = i_у = 0.

Вплив величини напруги джерела і параметрів ланцюга

Перехідний процес при зарядці конденсатора від джерела постійної напруги характеризують три показники: стала напруга на конденсаторі, початкова швидкість зміни напруги, постійна часу; при зміні напруги джерела змінюються стала напруга на конденсаторі і початкова швидкість зміни напруги, а постійна часу ланцюга від напруги не залежить. На рис.3.13 приведені (відповідно двом різним напругам джерела U₁ і U₂ ) графіки зміни напруги на конденсаторі.

Рисунок 3.13 – Графіки перехідної напруги на конденсаторі при різних напругах джерела

Зміна ємності впливає на тривалість перехідного процесу так само, як зміна опору (рис.3.14).

Рисунок 3.14 – Графіки перехідних напруг і струму конденсатора при різних величинах ємності

Перехідний процес при розрядці конденсатора

Перехідний процес при розрядці конденсатора ілюструється схемою рис.3.15.

Рисунок 3.15 – Схема розрядки конденсатора

Після перемикання перемикача конденсатор не може розрядитися миттєво, тобто напруга u_C не може зменшитися стрибком до нуля, а підтримується протягом перехідного періоду за рахунок енергії, накопиченої в електричному полі конденсатора; при цьому в активному опорі R здійснюється необоротний процес перетворення електричної енергії в теплову..

Напруга на конденсаторі при розрядці виражається рівнянням

,

де..τ = RC – постійна часу ланцюга.

Тривалість перехідного процесу, як і при зарядці, теоретично рівна нескінченності, а практично розрядка вважається закінченою при t = (4÷5) τ.