2.1) Природний паралелізм незалежних задач

Полягає в тому, що в систему поступає попередній потік незвязаних між собою задач , тобото розвязання будь-якої задачі не залежить від результатів розвязання задач інших задач.

У цьому випадку використовується декілька пристроїв обробки підвищує продуктивність системи.

2.2) Паралелізм незалежних гілок

Полягає у тому, що при розвязанні великої задачі може бути виділені окремі незалежні частини гілки програми, які при наявності декількох пристроїїв обробки можуьб виконуватися паралельно та незалежно один від одного.

Двома незалежними гілками програми будемо вважати такі частини задачі при виконанні яких виконуються наступні умови

1. Ні одна із вхідних для гілки програми величин не є вихідною величиною іншої програми

2.Для обох гілок програми не можуть робитися запис у одні і такі самі комірки памяті

3.Умови виконання одної гілки не залежать від результатів, або ознак, отриманих при виконанні іншої гілки

4.Обидві гілки мусять виконуватися за різними блоками програми.

Добре уявлення про паралелізм незалежних гілок дає ЯПФ – ярусна паралельна форма програми, приклад якої наведемо на рис.

Програма представлена у вигляді сукупності гілок, розміщених на декількох рівнях – ярусах.

Кругами з цифрами в середині позначені гілки.

Стрілками позначені вхідні дані та результати обробки.

Вхідні дані позначені символом Х. а вихіні дані символом У.

Символи Х мають нижні цифрові індекси, які позначають номера вхідних величин.

Символі У мають цифрові позначення знизу і вгорі, цифри вгорі відповідають номеру гілки , при виконанні якої отриманий даний результат, а цифра а знизу біля У визначає порядковий номер результату , який отриманий при реалізації даної гілки програми.

Зображена на малюнку програма має 14 гілок які розміщені на 5 ярусах .

Гілки кожного ярусу не пов’язані одна аз одною, тобто результати розміщення будь-якої гілки даного ярусу не є вхідними даними для іншої гілки цього ж ярусу.

Граф схема і фрази:

На цьому ж графі можуть бути зображенні і зв’язки за керуванням або пам’яттю. У цьому випадку граф-схема дозволяє наочно показати повністю незалежні гілки. Для простоти зображення ми цього не робимо.

На прикладі цієї досить простої програми можна виявити переваги КС, яка залучає декілька пристроїв обробки та проблеми , які при цьому виникають.

Приклад:

Довжина і-тої гілки представлена числами часових одиниць t_i , які необхідні для її виконання .

Для одного обчислювального засобу(компа)

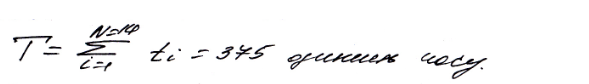
Якщо уявити що програм авиконується двома пристроями обробки , що працюють незалежнаа один від одного то час рішення задачі скоротиться. Але заральний час рішення задачі буде різний у залежності від послідовності виконання незалежних гілок.

Розглянемо 3 варіанти даної ЯПФ:

Варіант 1 :

Процесор 1 виконує гілки 1,4,5,9,10,13

Процесор 2 виконує гілки 2,6,3,7,8,12,13,14

При цьому проц.1 витрачає 145 одиниць часу, з яких 55 простоює.

Процесор 2 витрачає 230 одниць часу .

Варіант2:

Процесор 1 виконує гілки 1,4,5,9,10,11,13

Процесор 2 виконує гілки 2,6,3,7,8,12,14

При цьому проц.1 витрачає 160 одиниць часу, з яких 25 простоює.

Процесор 2 витрачає 215 одниць часу .

Варіант3:

Процесор 1 виконує гілки 1,4,8,12,11,13

Процесор 2 виконує гілки 2,6,3,7,9,10,14

При цьому проц.1 витрачає 1175 одиниць часу,

Процесор 2 витрачає 200 одниць часу з яких 5 простоює.

Розглянуті 3 варіанти: замість 375 одиниць часу , в 1 вар.-230, в 2вар.-215 , в 3вар.-200 одиниць часу отримали замість 375 отримали 200.

Для того щоб із допомогою декількох пристроїв обробки розв’язати задачу яка має незалежні паралельні гілки необхідно організувати програму яка визначає шляхи розв’язання задачі та виробляє інформацію про готовність кожної гілки.

Все це відносно легко реалізувати коли достатньо точно відомо тривалість виконання кожної гілки. На практиці це буває досить рідко (дуже рідко). В кращому випадку відома наближена довжина гілки. Тому організація оптимального графіка роботи є досить складною задачею.

Як правило важко уникнути деяких простоїв, які виникають за відсутності початкових даних для виконання гілки. Все це призводить до того що виграш в продуктивності системи трохи знижується.

Тобто проблема є. Але при розв’язанні багатьох складних задач тільки програмування із виділенням незалежних гілок дає можливість істотно скоротити час розв’язання.

Добре піддаються паралельній обробці задачі шотирна алгебра , лінійне програмування , спектральна обробка сигналів , прямі та зворотні перетворення Фур’є.

2.3 ПАРАЛЕЛІЗМИ ОБ’ЄКТІВ АБО ДАНИХ.

Має місце тоді коли за одною і того самою програмою мусить оброблятися деяка сукупність даних, які надходять в систему одночасно.

ПРИКЛАДИ:

1 задача обробки сигналів РЛС(радіо-локаційних станцій) : всі сигнали обробляються за одною і тою самою програмою.

2. обробка інфи від давачів які вимірюють одночасно один і той самий параметр і які встановлені на декількох однотипних об’єктах.

Ці програми можуть бути різної складності які мають декілька операцій до сотні і тисячі операцій.

3. це можуть бути і суто математичні задачі (наприклад задачі векторної алгебри).розв’язання задач при цьому зводиться до виконання однакових операцій над парами чисел двох аналогічних об’єктів.

Нариклад : 1) завдання двох матриць розрядності (nxm)

При цьому операція додавання над (nxm) парами чисел .

2). Добуток матриці розрядністю (nxm) зводиться до виконання (nxm) множень елементів матричні на скаляр .

Всі ці операції як + така і * можуть виконуватися паралельно та незалежно одна від одної декількох пристроями обробки.

3). Конвеєрна обробка інформації.

Може бути реалізована у системі і з одним процесором який поділений деяке число послідовно включених операційних блоків, кожен з яких спеціалізований на виконання чітку результатіо визначеної частини операцій у результаті створюється свого роду конвеєр обробки.

ПРИКЛАД КОНВЕЄРА:

Операція додавання двох чисел з рухомою комою.

Може поділити операцію на 4 етапи, які виконуються послідовно:

1. Порівняння порядків

2. Вирівнювання порядків (зсув мантиси з меншим порядком для вирівнювання з мантисою з більшим порядком).

3. Додавання мантис.

4. Нормалізація результату.

У відповідності зі схемою у складі процесора 4 операційні блоки поєднані послідовно, які реалізують 4 кроки операції додавання. Тобто блоки ПП,ВП,ДМ,НР.

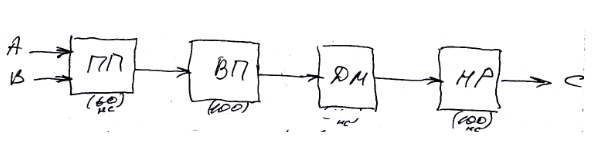
Час виконання кожного кроку приблизно =. Загальна сума операції додавання 400нс.

Припустимо що виникає задача додавання двох векторів які містять по n елементів з рухомою комою. Для розвязання цієї задачі вимагається додати два числа

Для того щоб не створювати черги операцій на обробку припустимо що час виконання кожного з цих етапів одинаковий і рівний максимальному значенню

Робити всі команди конвеєра цикловими по часу

Однак в результаті 1 результат ми отримали на конвеєрі за 560 нс.

Але наступні результати будуть отримуватися за 140 нс.