Вариант 1

I. Найдите предел последовательности обобщённых функций.

f_n(x)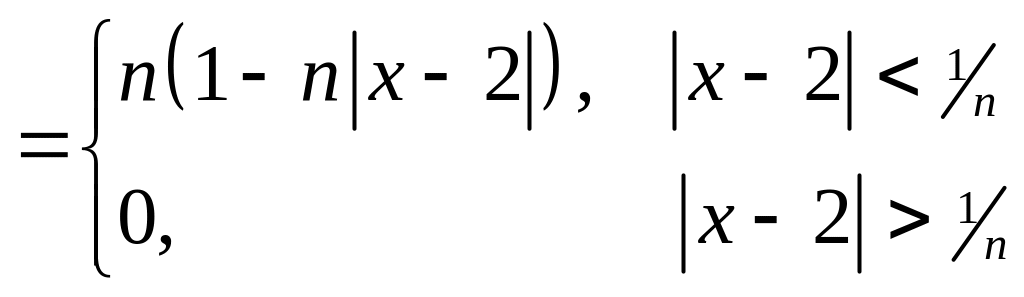

II. Найдите указанные обобщённые производные.

1) , где f(x) из п. I, в . 2) , где f(x,y) , в

III. Найдите свёртки обобщённых функций.

1) в .

2) , в .

IV. Решите методом потенциалов обобщённые задачи Коши: 1) № 12.53.1, 2) № 13.17.1.

V. Решите методом потенциалов задачу о стационарном распределении температуры при данной плотности f источников тепла в области.

ИЦП, , .

VI. Решите смешанную задачу с помощью преобразования Лапласа.

, ,

.

VII. Решите стационарную задачу с помощью функции Грина.

Вариант 2

I. Найдите предел последовательности обобщённых функций.

f_n(x)

II. Найдите указанные обобщённые производные.

1) , где f(x) , в .

2) , где f(x,y) в

III. Найдите свёртки обобщённых функций.

1) в .

2) , в .

IV. Решите методом потенциалов обобщённые задачи Коши: 1) № 12.53.2, 2) № 13.17.2.

V. Решите методом потенциалов задачу о стационарном распределении температуры при данной плотности f источников тепла в области.

ЕЦП, , .

VI. Решите смешанную задачу с помощью преобразования Лапласа.

, ,

.

VII. Решите стационарную задачу с помощью функции Грина.

Вариант 3

I. Найдите предел последовательности обобщённых функций.

f_n(x)

II. Найдите указанные обобщённые производные.

1) , где f(x) , в .

2) , где f(x,y) , в

III. Найдите свёртки обобщённых функций:

1) в .

2) , в .

IV. Решите методом потенциалов обобщённые задачи Коши: 1) № 12.53.3 2) № 13.17.6.

V. Решите методом потенциалов задачу о стационарном распределении температуры при данной плотности f источников тепла в области.

ИШП, , .

VI. Решите смешанную задачу с помощью преобразования Лапласа.

, ,

.

VII. Решите стационарную задачу с помощью функции Грина.

Вариант 4

I. Найдите предел последовательности обобщённых функций.

f_n(x)

II. Найдите указанные обобщённые производные.

1) , где f(x) , в . 2) , где f(x,y) , в

III. Найдите свёртки обобщённых функций

1) в .

2) , в .

IV. Решите методом потенциалов обобщённые задачи Коши: 1) № 12.53.4 2) № 13.17.5.

V. Решите методом потенциалов задачу о стационарном распределении температуры при данной плотности f источников тепла в области.

ЕШП, , .

VI. Решите смешанную задачу с помощью преобразования Лапласа.

, ,

.

VII. Решите стационарную задачу с помощью функции Грина.

Вариант 5

I. Найдите предел последовательности обобщённых функций.

f_n(x)

II. Найдите указанные обобщённые производные.

1) , где f(x) , в . 2) , где f(x,y) в

III. Найдите свёртки обобщённых функций

1) в .

2) , в .

IV. Решите методом потенциалов обобщённые задачи Коши: 1) № 12.53.5 2) № 13.17.4.

V. Решите методом потенциалов задачу о стационарном распределении температуры при данной плотности f источников тепла в области.

ИЦТ, , .

VI. Решите смешанную задачу с помощью преобразования Лапласа.

, ,

VII. Решите стационарную задачу с помощью функции Грина.