4.2.3 Метод внутренней нормы доходности.
Значение внутренней нормы доходности (Internal Rate of Return, IRR) характеризует процентную ставку, при которой чистый дисконтированный доход NPV равен нулю. Значение IRR определяется по следующей формуле:
NPV=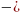
IC+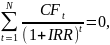
(4.2.2)
или
IC =
.
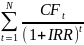(4.2.3)
4.3 Использование теории принятия решений для анализа инвестиционных проектов
Поскольку выбор наилучшего инвестиционного проекта является задаче выбора вариантов из данного множества альтернатив при условии определенности, для ее решения целесообразно воспользоваться методами теории принятия решений.
В рамках принятия решений в условиях определенности справедлива следующая модель задачи принятия решений:
X – множество альтернатив (инвестиционных проектов);
Y – множество исходов;
;
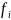Y – R,
i=1,…,m
– множество критериев (показателей
качества, где R –
множество вещественных чисел;
ф: X – Y – детерминистская функция, отображающая множество альтернатив во множество исходов.
Таким образом, предполагается, что
каждому решению x G
X соответствует
единственный элемент y
G Y,
где y= ф(x).
Исходы y оцениваются
m числами в соответствии
с зависимостью
.
Предполагается, что каждую из функций
необходимо максимизировать (в противном
случае выполняется замена
).
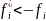С помощью суперпозиции
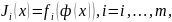(4.3.1)
можно непосредственно оценивать качество решения x. Кроме того, можно работать с векторным отображением
J: x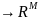
,
J = (
.
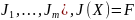
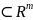(4.3.2)
Задание бинарного отношения R
на множестве исходов Y
индуцирует соответствующее бинарное
отношение
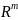на
множестве X:
(
.
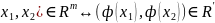(4.3.3)
Соответственно возникает бинарное
отношение
на множеств оценок
:
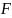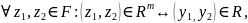(4.3.4)
где
,
.
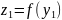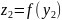Из приведенных выражений следует, что в условиях определенности (данное условие выполняется в случае выбора инвестиционного проекта) отношения предпочтения могут задаваться в любом из множеств X, Y, F. Обычно в качестве основного рассматривается отображение
J: X
,
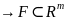(4.3.5)
т. е. системы предпочтений задаются во множествах X и F.
В задаче выбора инвестиционного проекта рассматривается многокритериальная оптимизация вида
.
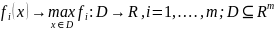(4.3.6)
Выражение (4.3.6) подразумевает, что заодно
m функций
,отображающих
множество D n-мерных
векторов x=(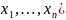
во множестве вещественных чисел R.
Предполагая, что выбор оптимальных
значений x производится
не по всем n-мерном
пространстве
,
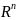а в некотором его подмножестве D.
Существует ряд методов решения задачи
(4.6), основные из некоторых приведены
ниже.
4.3.1 Метод главного критерия.
В методе главного критерия в качестве
целевой функции выбирается один из
функционалов
(обычно функционалы индексируются таким
образом, чтобы им оказался
),
который наиболее полно отражает цель
принятия решения. Остальные требования
к результату, описываемые функционалом
,
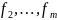учитываются с помощью введения
дополнительных ограничений. Таким
образом, задача (4.3.6) сводится к следующей:
,
.
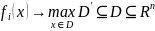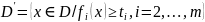(4.3.7)
Метод главного критерия может быть
расширен в случае допустимости принятия
более одного решения. Это расширение
может быть полезно, когда значение
,
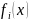x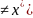
удовлетворяет нижеследующему условию
(4.3.8)) близки к значению
.
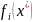В этом случае критерий можно переписать
в виде
,
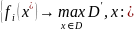. (4.3.8)
Значение
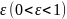определяет степень близости допустимых
альтернатив. Назначение главного
критерия и допустимых ограничений на
остальные частные критерии – задача
лица, принимающего решение. Очевидно,
что этот шаг оказывает решающее влияние
на результат выбора окончательного
решения.
Необходимо отметить, что, несмотря на то что задача (4.3.8) не эквивалентна задаче (4.6), ее решения достаточно для обоснования решений.