30. Циклічний зсув на 1 елемент вліво
|shift_R
0
n-1
А є R
k є R
n,i є N
введення масиву A[n]
k=А[0]
+1
(i=0,n-2)
А[i]=A[i+1]
А[n-1]=k
виведення масиву А[n]
|end
33. Циклічний зсув на 1 елемент вправо
n-1 n-2 2 1 ітерації
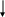
a0
a2
a3
…
an-2
an-1
An
А:
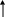
an-1
an-1
a0
a1
…
an-3
an-2
an-1
А:
Пересилання елементів зручно виконувати справа-наліво (від останнього елементу до першого), щоб не загубити попередні значення і скоротити кількість присвоєнь. Значення A[n-1] завчасно слід запам’ятати в допоміжній змінній.
|shift_R
0 n-1
А є R
k є R
n,i є N
введення масиву A[n]
k=А[n-1]
-1
(i=n-2,1)
пересувається в зворотному напрямку,
А[i+1]=A[i] крок від’ємний
А[0]=k
виведення масиву А[n]
|end
36. Циклічний зсув на k елементів вліво
перший варіант полягає в тому, щоб використати існуючий алгоритм зсуву на один елемент і в циклі організувати k таких зсувів.
|shift_k
0 n-1
А
є R
В є R
n,i,j,k є N
введення k,А[n] Однак, при збільшенні кількості зсувів
значно збільшується час роботи,
(j=0,k-1)
постійно виконуються непродуктивні
В=А[0] проміжні зсуви.
+1
(i=0,n-2)
А[i]=A[i+1]
А[n-1]=B
виведення А[n]
|end
Можна уникнути великої кількості проміжних пересилань, якщо використовувати допоміжний масив, в якому елементи одразу ж будуть розміщуватись на необхідному місці. В цьому випадку для кожного елемента будуть потрібні лише дві операції привласнення.
|Shift_k
0 n-1
A,B
є R
n,i,k є N
введення n, A, k
(i=k,n-1) пересилка до допоміжного масиву останніх
B[i-k]=A[i] n-k елементів
(i=0,k-1) пересилка перших k елементів до допоміжного
B[n-k+i]=A[i] масиву
(i=0,n-1) пересилки елементів, що зсунуті на k позицій
A[i]=B[i] із допоможного масиву у вихідний
виведення А
end
Однак запропонований алгоритм вимагає великого допоміжного масиву, викликає нераціональне використання пам’яти ЕОМ.
В останньому алгоритмі також буде потрібен допоміжний масив, але розмірність цього масиву дорівнює кількості зсувів. В цьому масиві ми збережемо перші (у випадку зсуву вліво) або останні (у випадку зсуву вправо) k елементів.
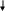
1
2 3 . . .
k
k+1
k+2 . . .
n-k+1
.
. .
n
A:
<-
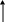
масив
1
k
B:
|Shift_k
1
k
B є R
1 n
A є R
n,i,k є N
введення A, k
(i=0,k-1)
B[i]=A[i] пересилка перших k елементів
(i=k,n-1)
А[i-k]=A[i] зсув n-k елементів, що залишились
(i=0,k-1)
A[n-k+i]=B[i] запис перших k елементів у кінець масиву
виведення А
|end
}