Индексы, использующие взвешивание арифметических и геометрических величин.
К таким индексам относятся два различных индекса, рассчитываемые компанией Value line.
Все индексы отражают рост и падение соответствующей группы ценных бумаг, однако они сильно отличаются друг от друга. Поэтому при использовании индексов важно учитывать их специфику.
Определим соотношение оцениваемой информации и количество оцениваемых чисел в указанных индексах, считая что в распоряжении имеются данные за предыдущие 25 лет:
Для индекса Доу – Джонса – имеются следующее количество данных:
25(лет)*4(квартала)*30(бумаг)=3000 чисел
Требуется
оценить
чисел.
Используя 3000 чисел можно достаточно
достоверно оценить 480 чисел.
Для индекс “Standart and Poor’s” данных 50000, а требуется оценить 125000 чисел, что, конечно в принципе невозможно.
Для индекс “Wilshire” данных 50000, требуется оценить 125000 чисел!.
Таким образом прямой статистический анализ можно применять лишь для оценки эффективности и ковариации небольшого числа ценных бумаг. Если составить оптимальный портфель, то риск из такого оптимального портфеля будет большим, а эффективность – маленькой по сравнению с оптимальным портфелем, составленным из всех ценных бумаг.
Итак, применение прямого статистического метода приводит к необходимости формирования портфеля ценных бумаг с завышенным риском и заниженной эффективностью, в то же время его использование для формирования портфеля, когда число независимых ценных бумаг несколько сотен или больше, в принципе, математически некорректно.
Более того, использование этого метода при анализе финансового рынка также некорректно для профессиональных индексов. Достоинством метода прямого статистического анализа является логическая и вычислительная простота, поэтому он применяется для учебных задач.
Метод прямого статистического анализа используется на практике только для оценки эффективности ценных бумаг, а матрица ковариации считается с использованием других методов, например, с использованием метода ведущих факторов.
9.2.Метод ведущих факторов.
Метод ведущих факторов основан на методе наименьших квадратов. Рассмотрим простейший вариант метода наименьших квадратов, в случае, когда ведущий фактор один, уравнение регрессии – линейное.
Имеется n – данных неизвестной функциональной зависимости между x и y
Построим линейную функцию:
,
которая наименее откланяется от табличных данных.
Таким образом, задача заключается в том, чтобы найти такие параметры и при которых прямая менее всего отклоняется от всех точек одновременно.
Р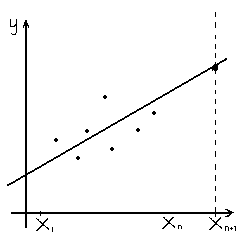
ис.1.Геометрическая
интерпретация метода наименьших
квадратов.
Математически это приводим к следующей задачи минимизации:
Минимум достигается там, где градиент функции f равен нулю.
Преобразуем первое уравнение:
Окончательно
(74)
Преобразуем второе уравнение
Окончательно
(75)
Получим
два уравнения (74), (75) для двух неизвестных
(
и
).
Расчеты удобно проводить с помощью таблицы, записывая вместо *, рассчитанные величины:
1 |
2 |
3 |
… |
n |
|
|
|
|
|
|
|
… |
|
* |
- |
- |
- |
|
|
|
… |
|
- |
- |
* |
- |
|
|
|
… |
|
- |
* |
- |
- |
|
… |
… |
… |
|
- |
- |
- |
* |
Из уравнения (1) и (2) следует, что
(76)
,
где
Запишем формулу (76) в более удобной форме.
Лемма1. Для любых n, xi ,yi ,i=1,…,n справедливо тождество:
(77)
Доказательство:
Обозначим
и запишем
и сумму в правой части (77) с использованием
евклидового скалярного произведения:
,
что и требовалось доказать.
Лемма доказана.
Положим
в (77)
получим, что справедливо следующее.
Следствие1.
Для любых
справедливо тождество:
Следствие2.
Обозначим:
,
вариация
данных по
,
,
ковариация
данных по
и
,
тогда
(78)