
Российский Государственный Университет нефти и газа
им. И.М.Губкина
Кафедра: Нефтяной и подземной гидромеханики
Курсовая работа
по теме:
«Гидродинамический расчет совместной работы пласта и скважины»
Выполнила: студентка группы АМ-09-6
Орехова Л.В.
Специальность: прикладная математика
Проверила: доц. Разбегина Е. Г.
Москва 2012 г.
Оглавление
Постановка задания 3
Исходные данные 3
Схема совместной работы пласта и скважины, несовершенной по степени вскрытия 4
Теория 5
Расчеты и графики 8
Заключение 13
Список литературы 14
Постановка задания
В однородном
круглом пласте постоянной толщины
эксплуатируется гидродинамически
несовершенная по степени вскрытия
скважина на стационарном режиме. Подъем
жидкости производиться по
насосно-компрессорным трубам при
закрытом сверху затрубном пространстве,
где жидкость и газ находятся в
гидростатическом равновесии. Требуется
найти зависимость дебита скважины Q
и затрубного давления Pз
от степени вскрытия пласта h
= b/h
скважины.
Исходные данные
СИ:
Радиус контура питания |
Rk =1км |
Rk = 1000 м |
Толщина пласта |
h=10 м |
h = 10м |
Диаметр насосно-компрессорных труб |
d = 5 см |
d = 0,05 м |
Шероховатость стенок труб |
∆ = 0,1 мм |
∆ = 10-4 м |
Высота столба газа в затрубном пространстве до начала эксплуатации скважины |
hro = 120м |
hro = 120м |
Проницаемость пласта |
k = 200 мД |
k = 204*10-15 м2 |
Плотность жидкости |
ρж = 850 кг/м3 |
ρж = 850 кг/м3 |
Плотность газа при нормальных условиях |
ρro = 1,5 кг/м3 |
ρro = 1,5 кг/м3 |
Вязкость жидкости |
μж = 4 спз |
μж = 4*10-3 Па*с |
Устьевое давление |
Pу = 5 ат |
py = 5*105 Па |
Показания манометра в затрубном пространстве до начала эксплуатации |
Pзо = 50 ат |
Pзо = 50*105 Па |
Глубина залегания пласта |
H = 2 км |
H = 2000м |
Радиус скважины |
rc=100 мм |
rc=0,1 м |
Схема совместной работы пласта и скважины, несовершенной по степени вскрытия
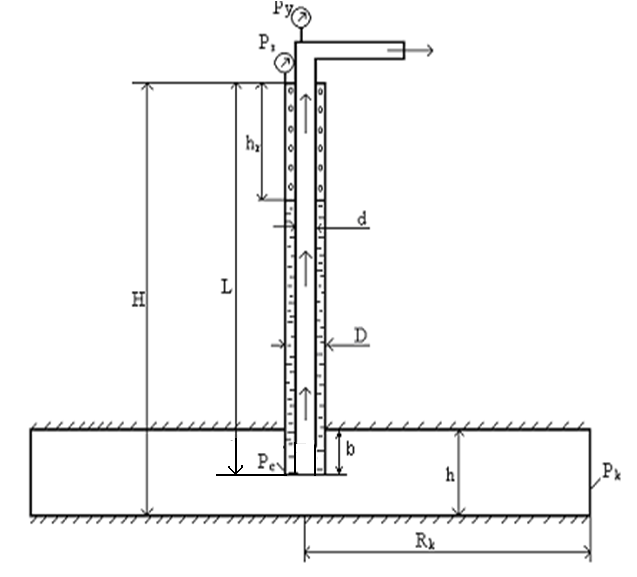
Теория
Потери напора при подъеме жидкости по насосно-компрессорным трубам
Потери напора
при подъеме жидкости по насосно-компрессорным
трубам h1-2=
h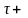 hm,
h
hm,
h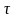 -потери
по длине трубы, hm-потери
на местные сопротивления. При решении
задачи мы пренебрегаем потерей энергии
на местные сопротивления (hm).
Потери напора на трение при движении
вязкой жидкости в трубе рассчитываются
по формуле Дарси-Вейсбаха:
-потери
по длине трубы, hm-потери
на местные сопротивления. При решении
задачи мы пренебрегаем потерей энергии
на местные сопротивления (hm).
Потери напора на трение при движении
вязкой жидкости в трубе рассчитываются
по формуле Дарси-Вейсбаха:
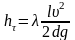 - формула
Дарси-Вейсбаха,
(1)
- формула
Дарси-Вейсбаха,
(1)
где:
- коэффициент гидравлического сопротивления;
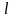 -
длина трубы;
-
длина трубы;
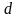 - внутренний диаметр
трубы;
- внутренний диаметр
трубы;
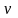 - средняя скорость
в поперечном сечении потока;
- средняя скорость
в поперечном сечении потока;
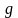 - ускорение силы
тяжести;
- ускорение силы
тяжести;
Коэффициент гидравлического сопротивления рассчитывается в зависимости от режима течения. Он зависит от безразмерного числа Рейнольдса (Re) и относительной шероховатости стенок труб (/d) и выражается различными формулами в зависимости от режима течения жидкости:
Коэффициент
гидравлического сопротивления λ в
зависимости от безразмерного числа
Рейнольдса
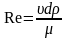 (1.2) и относительной шероховатости
(1.2) и относительной шероховатости
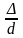 стенок трубы выражаются следующими
формулами:
стенок трубы выражаются следующими
формулами:
Число Рейнольдса |
Формула для вычисления коэффициента гидравлического сопротивления |
Режим течения |
Re ≤ 2320 |
|
Ламинарный |
|
|
Небольшая турбулетность (зона гидравлически гладких труб) |
|
|
Зона смешанного трения |
|
|
Квадратичная зона |

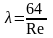
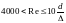
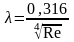 (формула
Блазиуса)
(формула
Блазиуса)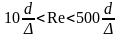
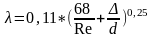 (формула
Альтшуля)
(формула
Альтшуля)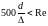
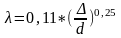 (формула
Шифренсона)
(формула
Шифренсона)