
- •Вопросы для самоподготовки
- •Решение систем линейных алгебраических уравнений
- •Метод Гаусса
- •Метод Гаусса-Зейделя.
- •2: Writeln ('Количество итераций выше допустимого');
- •Решение систем линейных уравнений
- •Метод простой итерации
- •Применительно к слау
- •Алгоритм
- •Метод Ньютона (метод касательных)
- •Одномерный случай
- •Многомерный случай
Метод простой итерации
В основе метода заложено понятие сжимающего отображения. Определим терминологию:
Говорят,
что функция ![]() осуществляет сжимающее
отображение на
осуществляет сжимающее
отображение на ![]() ,
если
,
если
Тогда основная теорема будет выглядеть так:
|
Теорема Банаха (принцип сжимающих отображений). Если — сжимающее отображение на , то:
|
|
Поясним
смысл параметра ![]() .
Согласно теореме
Лагранжа имеем:
.
Согласно теореме
Лагранжа имеем:
![]()
Отсюда
следует, что ![]() .
Таким образом, для сходимости метода
достаточно, чтобы
.
Таким образом, для сходимости метода
достаточно, чтобы ![]()
.........
и
так далее, пока ![]()
Применительно к слау
Рассмотрим систему:
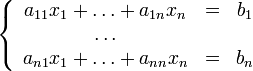
Для неё итерационное вычисление будет выглядеть так:
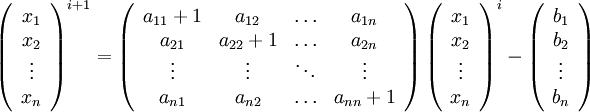
Сходимость
метода будет осуществлять 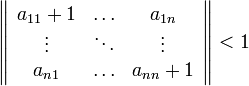
Следует отметить, что для оценки сходимости вычисляется не определитель матрицы, а норма матрицы. Поэтому в данном случае поставлены двойные вертикальные черты, а не одинарные.
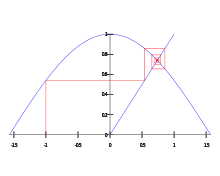
Решение уравнения cos(x)=x по методу простой итерации, очередная итерация: xn+1=cos xn, начальное приближение: x1 = -1
Алгоритм
Условие
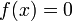 преобразуется
к виду
преобразуется
к виду 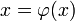 ,
где
,
где 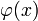 —
сжимающая
—
сжимающаяЗадаётся начальное приближение и точность
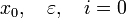
Вычисляется очередная итерация
Если , то
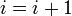 и
возврат к шагу 3.
и
возврат к шагу 3.Иначе
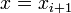 и
остановка.
и
остановка.
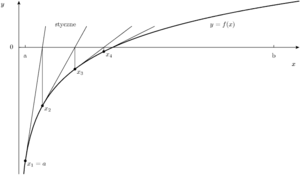
Решение уравнения f(x)=0 по методу Ньютона, начальное приближение: x1=a.
Метод Ньютона (метод касательных)
Основная статья: Метод Ньютона
Одномерный случай
Для
того, чтобы решить уравнение
,
пользуясь методом простой итерации,
необходимо привести его к виду
,
где
—
сжимающее отображение. Чтобы отображение
было наиболее эффективно, необходимо,
чтобы в точке очередной итерации ![]() выполнялось
выполнялось ![]() .
Будем искать решение данного уравнения
в виде
.
Будем искать решение данного уравнения
в виде ![]() ,
тогда:
,
тогда:
![]()
Воспользуемся
тем, что
,
и получим окончательную формулу для ![]() :
:
![]()
С учётом этого сжимающая функция примет вид:
![]()
Тогда алгоритм нахождения численного решения уравнения сводится к итерационной процедуре вычисления:
![]()
Многомерный случай
Обобщим полученный результат на многомерный случай.
Выбирая
некоторое начальное приближение ![]() ,
находят последовательные приближения
,
находят последовательные приближения ![]() путем
решения систем уравнений:
путем
решения систем уравнений:
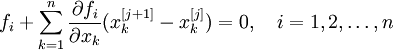 ,
,
где ![]() .
.
