8.2 Метод ожидаемых путей
Метод ожидаемых путей – приближённый графический метод и не имеет критериев оценки точности и достоверности. В соответствии с ним поле разбивается на элементарные объёмные фигуры: кольца, усечённые конусы, призмы и др. Общая ёмкость, проводимость определяются как совокупность ёмкостей, проводимостей каждого элементарного объёма.
9 Экспериментальные методы анализа электромагнитных полей
9.1Метод моделирования с помощью электрических сеток.
В соответствии с этим методом моделирования строится электрическая модель поля из большого числа элементов эквивалентной электрической цепи. Каждый элементарный объём поля приближённо заменяется резисторами, конденсаторами и катушками индуктивности. С помощью конденсаторов и катушек индуктивности учитываются токи смещения и ЭДС, индуцируемые переменным магнитным током. Метод может быть применён и для моделирования переменных электромагнитных полей и предполагает численное решение полевой задачи на ЭВМ.
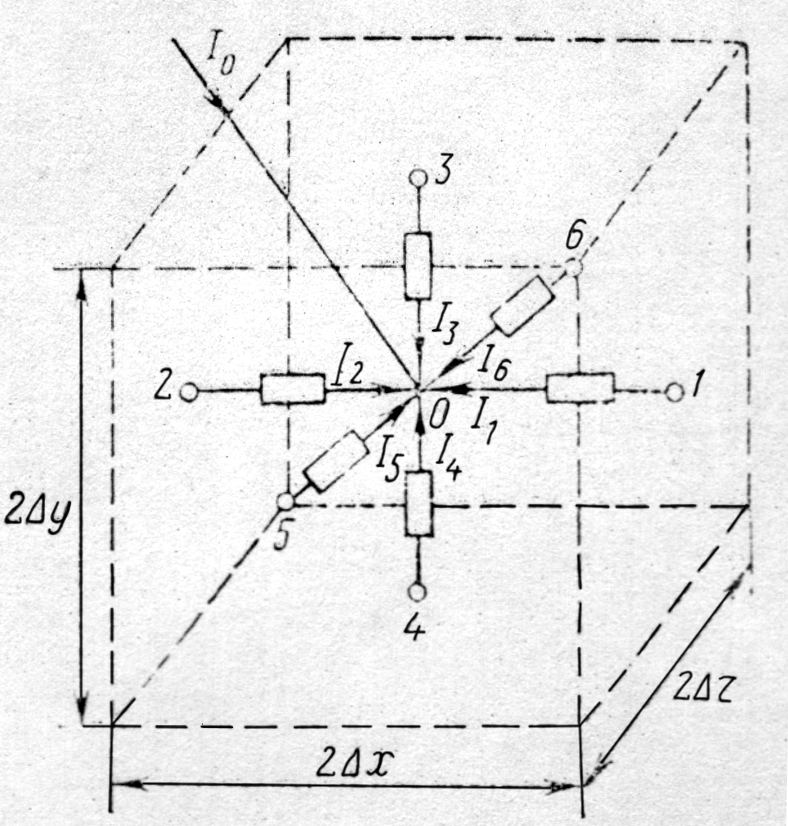
Распределение потенциала в поле проводящей среды находится путём моделирования этого поля с помощью электрических схем. Моделируемая сплошная электропроводящая среда с электрической проводимостью делится на элементарные объёмы, например кубы, каждый из которых представляется электрической схемой замещения. При моделировании постоянного (потенциального) поля схема замещения состоит из резисторов, которые располагаются по трём взаимно перпендикулярным координатным осям прямоугольной системы координат с началом в центре куба (рис. 3.6).
В центре куба резисторы соединяются в один узел O , а свободные концы 1–6 резисторов выводятся на грани куба и соединяются с резисторами соседних кубов. Сопротивления резисторов вычисляются по выбранному шагу сетки в направлении координатных осей x , y и z :
|
(3.19) |
При x = y = z = a все сопротивления равны R = 1 / ( 4 a ).
|
Рис. 3.6 Электрическая схема замещения элементарного объёма среды |
Сопротивления резисторов на поверхности электрической сетки в два раза больше сопротивлений резисторов внутри сетки: R x = x / / ( 2 y z ) = 1 / ( 2 a ) , а сопротивление на ребре куба сетки на границе поля вдоль линий тока в четыре раза больше: R x = ( 1 / ) x / / ( y z ) = 1 / ( a ) . Источники исходного поля моделируются источниками тока I 0 ( напряжения U ) путём присоединения их к общему узлу O или к внешним точкам сетки. При этом
I 0 = 4 J ( x , y , z ) x , y , z , |
(3.20) |
где J ( x , y , z ) – заданное распределение плотности тока источников. При x = y = z = a ток I 0 = 4 J ( x , y , z ) a 3 . В этом случае для каждой ячейки справедливо уравнение
1 + 2 + 3 + 5 + 6 – 6 0 = ( J / ) a 2 , |
(3.21) |
которое моделирует конечноразностное уравнение Пуассона.
Распределение потенциалов в электрической сетке описывается уравнением с точностью до частных производных четвёртого порядка от в проводящей среде, умноженных на a 2 / 4 !