2.3. Оценка однородности интервала бурения
Применение метода сравнения средних требует вычисления общего среднего квадратического отклонения полученных вариационных рядов по формуле
s12
=
(2.6)
(1 и 2 – индексы, соответствующие первому и второму вариационным рядам) и параметра распределения t12 разности |x1 – x2| по формуле
t12
=
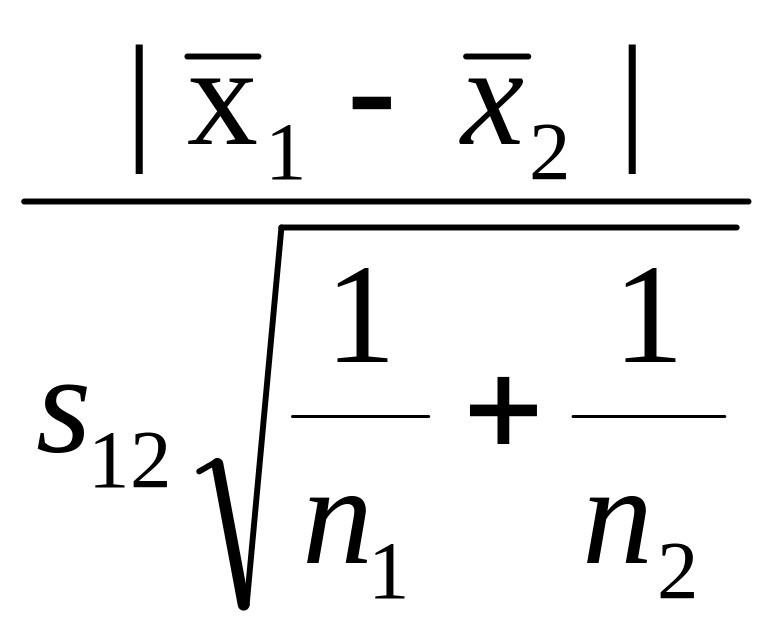. (2.7)
Вычисленное значение параметра t12 сравнить с критическим t(Р, f) распределения Стьюдента (табл. 2.4), соответствующим заданной вероятности и числу степеней свободы f, которое в данном случае вычисляется по формуле
5
f = n1 + n2 – 2. (2.8)
Таблица 2.4
Значения параметра Стьюдента t для одной случайной величины
при числе степеней свободы f
f |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
t |
4,30 |
3,18 |
2,78 |
2,57 |
2,45 |
2,36 |
2,31 |
2,26 |
2,23 |
2,20 |
2,18 |
Если t12 > t, то различие между сравниваемыми значениями средних статистически значимо, а интервал бурения неоднородный, и его выделенные части следует рассматривать отдельно. Если t12 < t, то различие статистически незначимо, рассматриваемый интервал бурения однородный, и его не следует делить на части. Последующие расчеты выполнить для той части интервала, толщина которого больше, а в случае однородного интервала – для обеих частей как одного целого.
3. Определение статистических характеристик показателей
МЕХАНИЧЕСКИХ СВОЙСТВ ГОРНОЙ ПОРОДЫ
Для большей по толщине части интервала бурения провести обработку всех вариационных рядов: провести отбраковку маловероятных значений и рассчитать среднее арифметическое значение и среднее квадратическое отклонение для всех характеристик горной породы. Если интервал бурения однородный, то расчеты выполнить для всего интервала бурения.
Далее следует определить нижнюю xн и верхнюю хв границы случайной величины, в пределах которых с заданной вероятностью лежат все ее значения:
(3.1)
где t – параметр распределения Стьюдента, значения которого приведены в табл. 2.4 при заданной вероятности 0,95.
В общем случае участвующих в расчетах независимых характеристик (значений случайных величин) может быть одна, две, три и более. В случае одной случайной величины параметр Стьюдента выбирается из табл. 2.4 , но число степеней свободы определяется по формуле
f = n – 1. (3.2)
Результаты расчетов характеристик вариационных рядов, а также нижних и верхних значений свести в таблицу по форме табл. 2.4.
Таблица 3.2
Статистические характеристики показателей механических свойств
и пористости горных пород
Обозначения |
р0, МПа |
рш, МПа |
С, МПа |
а21, мм/ч |
а25, мм/ч |
|
|
|
|
|
|
s |
|
|
|
|
|
хн |
|
|
|
|
|
хв |
|
|
|
|
|
Заполненная табл. 3.2 является основным результатом статистической обработки измерений показателей механических свойств горной породы и ее пористости. Она содержит исходные данные для дальнейших расчетов.