3.4. Дополнение: сопряжения, выполняемые посредством коник

Кривые 2-го порядка (коники) широко применяются в технике строительстве и архитектуре. Форма коники и её положение на плоскости определяются заданием пяти параметров, например, пятью касательными, никакие три из которых, не должны пересекаться в одной точке или пятью точками, никакие три из которых не должны лежать на одной прямой. В число пяти параметров может входить любая комбинация из касательных и точек, отвечающих указанным выше условиям.

При задании коники пятью параметрами вид кривой (эллипс, парабола или гипербола) предусмотреть заранее трудно. Поэтому кривую удобнее задавать двумя касательными к ней с точками касания на них и графическим или инженерным дискриминантом.

Пусть касательные t_a и t_b касаются кривой в тт. А и В и пересекаются в т. М (рис. 52).

Найдём середину Т хорды АВ и проведём медиану МТ. Выберем на медиане некоторую точку N и зададим тем самым значение дискриминанта. Тогда коника может считаться заданной.

Дискриминантом f коники называется отношение отрезков NM к ТМ, т.е. f= NM/ ТМ. При этом, если f <0,5, то кривая будет эллипсом, если f = 0,5 – параболой, а если f >0,5 – гиперболой.

Задача 1. Построить некоторое множество текущих точек кривой k, которая определена парой касательных с точками А и В на них и дискриминантом f= NM/ ТМ (рис. 53) .

Поскольку при подсчёте величина дискриминанта окажется, в нашем случае, равной f = 0,42, то искомой кривой будет эллипс. Для построения эллипса необходимо отыскать некоторое множество его текущих точек в следующем порядке:

1. Проводим прямые a =А 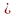N и b = В N.

2. Через т. М проводим произвольную прямую l, которая пересечёт прямые

a и b соответственно в точках 1 и 2.

3. Точку Е кривой находим на пересечении прямых с (А-2) и d (В-1).

4. Пучок прямых lⁱ c центром в т. М позволяет найти сколько угодно

точек Еⁱ кривой при аналогичных построениях.

Рис. 52 Рис. 53

Задача 2. Построить арочную кривую, которая определена парой взаимно-параллельных касательных t_a и t_b с точками касания А и В на них и точкой N подъёма (рис. 54).

Поскольку дискриминант f= N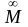 / Т , при несобственной точке будет f <0,5, то арочный свод – эллиптическая кривая. Таким образом АВ – большая ось эллипса, TN – его малая полуось и нахождение его текущих точек окажется аналогичным предыдущей задаче.

1. Проводим прямые a =А N и b = В N.

2. Между А и В проводим произвольно прямую l║ТN, которая пересечёт

прямые a и b соответственно в точках 1 и 2.

Рис. 54

3. Точку Е кривой находим на пересечении прямых А-2 и В-1.

4. Переместив прямую l в положение l', аналогичными построениями

найдём ещё одну текущую т. Е' и т.д. Пучок параллельных прямых lⁱ,

проходящих через несобственную т. позволяет найти сколько

угодно точек Еⁱ кривой.