3.3. Построение циркульных спиралей

Точка, которая вращается в плоскости около некоторого центра и удаляется от него по определённому закону, описывает траекторию, представляющую собою спираль. Спирали относятся к односвязным линиям, не имеющим никаких разветвлений и простирающимся до бесконечности. Спирали широко используются в архитектурном декоре и имеют долгую художественную и сакральную традицию.

Циркульная спиральная кривая, состоящая из последовательных сопряжённых дуг, называется завитком.

Задача 1. Построить завиток по двум центрам 1 и 2 – концам заданного отрезка (рис. 45).

1. Из центра 1 проводим полуокружность 1'-2 радиуса R₁, равного величине исходного отрезка 1-2.

Рис. 45 Рис. 46

2. Из центра 2 проводим полуокружность 1'-2' радиуса R₂.

3. Из центра 1 проводим полуокружность 2'-1' радиуса R₃.

Дальнейшие построения аналогичны и их легко понять из чертежа.

Задача 2. Построить завиток по трём центрам 1, 2 и 3 – вершинам равностороннего треугольника (рис. 46).

1. Из центра 1 проводим дугу 3-1', равную трети окружности радиуса R₁.

2. Из центра 2 проводим дугу 1'-2', равную трети окружности радиуса R₂.

3. Из центра 3 проводим дугу 2'-3', равную трети окружности радиуса R₃.

Дальнейшие построения несложно продолжить аналогичным образом.

Задача 3. Построить завиток по четырём центрам 1, 2, 3 и 4 – вершинам квадрата (рис. 47).

Рис. 47 Рис. 48

1. Из центра 1 проводим дугу 4-1' радиуса R₁, равного стороне исходного квадрата.

2. Следующую дугу 1'-2' радиуса R₂ проводим из центра 2.

3. Очередную дугу 2'-3' проводим из центра 3 радиусом R_3.

Далее построения выполняются сходным образом, при этом на каждом этапе центры сопряжения сменяются последовательно (в данном случае, по часовой стрелке).

Построение шестицентрового завитка предлагается разобрать самостоятельно (рис. 48).

Задача 4. Построить завиток по заданному диаметру 4-4' окружности с известным центром О (рис. 49).

Рис. 49

1. Поделим заданный диаметр 4-4' на n равных частей по n/2 на радиус.

2. Тогда при n=8 радиусом R₁=1-4' из точки 1 проводим

полуокружность 4'–А.

3. Радиусом R₂ =1'-А из точки 1' проводим полуокружность АD.

4. Далее из центра 2 проводим полуокружность DB радиусом R₃ = D-2.

Последующие построения проводятся аналогичным образом.

Задача 5. Построить завиток по заданному отрезку ОА, где О – центр завитка (рис. 50a, b).

1. Делим отрезок ОА на n равных частей, например на n=9.

2. Около центра О описываем окружность радиуса, равного 1/9 ОА,

и вписываем в неё квадрат 1-2-3-4 (обход вершин против часовой

стрелки).

a) b)

Рис. 50

3. Соединяем середины сторон полученного квадрата и, таким образом,

находим ещё один квадрат, вписанный в предыдущий, в который, в свою очередь, аналогичным образом вписываем очередной квадрат 5-6-7-8 (обход вершин также против часовой стрелки) и т.д. (рис. 50b).

4. Строим дугу 9-А радиуса R₁= 1-9 из центра 1; т. А лежит на продолжении

стороны квадрата 1-2.

5. Строим дугу АВ радиуса R₂=2-А, причем т. В лежит на продолжении

стороны 2-3 квадрата. Далее построения ведутся аналогичным образом.

Точку Е стыка двух смежных дуг радиусов R₄ и R₅ находим на продолжении отрезка 4-5.

Спираль можно строить также на основе золотого прямоугольника (рис. 51), в котором отношение большей стороны к меньшей равно золотой пропорции , т.е.

АВ/ВС = 1+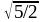

В этом прямоугольнике его стороны АВ и DC делятся точками О и Т₁ в отношении 5/3. В результате прямоугольник оказывается разделённым на квадрат АОТ₁ D и прямоугольник ОВСТ₁ стороны ОТ₁ и ВС которого, в свою очередь, так же делятся в отношении 5/3. Очередной и последующие прямоугольники продолжают делить аналогичным образом.

Рис. 51

В каждом квадрате, полученном таким образом, можно последовательно провести дуги окружностей из центров О, О₁, О₂, О₃, О₄, О₅, …, которые образуют завиток, построение которого традиция приписывает Архимеду.