Модальный регулятор

Является методом корневого синтеза, а именно, по желаемому расположению корней характеристического уравнения на комплексной плоскости строится модальный регулятор, который представляет собой коэффициенты отрицательной обратной связи по каждой динамической переменной.

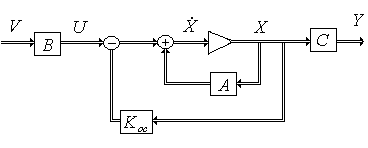
Рис. 3. Структурная схема системы управления с модальным регулятором.

Дано описание объекта:

(7)

Задаёмся видом желаемого полинома D_жел(p) – в соответствии с заданными (желаемыми) показателями качества.

Введём обратную связь, вида:

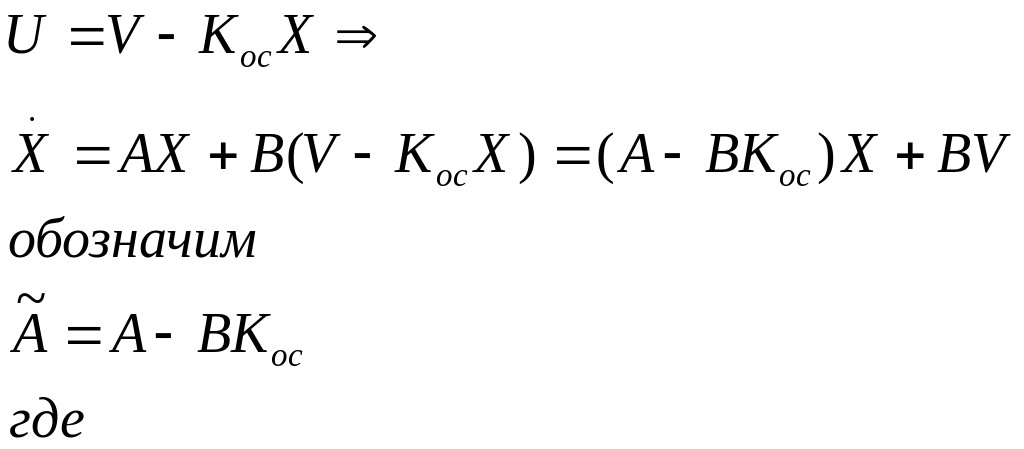
тогда можно найти из уравнения

(8)

где - характеристическое уравнение системы с регулятором.

Синтез цифрового пид-регулятора системы

В непрерывных системах широко используются PID-регуляторы, которые представляются идеализированным уравнением:

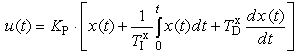(9).

где: K_P - коэффициент усиления пропорционального канала; T_I^x - постоянная времени сопрягающего полюса интегрального канала; T_D^x - постоянная времени сопрягающего полюса дифференциального канала.

Для малых периодов дискретизации T_ц уравнение может быть преобразовано в разностное без существенной потери в точности. Непрерывное интегрирование может быть представлено с помощью метода прямоугольников, или метода трапеций.

 Используем метод прямоугольников для аппроксимации непрерывного интеграла и запишем PID-закон в дискретном виде:

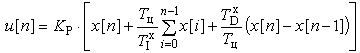(10).

В результате получен нерекуррентный (позиционный) алгоритм управления, который требует сохранения всех предыдущих значений сигнала ошибки x[i], и в котором каждый раз заново вычисляется управляющий сигнал u[n].

Для реализации программ закона регулирования на ЦВМ более удобным является рекуррентный алгоритм. Он характеризуется тем, что для вычисления текущего значения сигнала u[n] используется его предыдущее значение u[n-1] и поправочный коэффициент, не требующий существенных вычислительных затрат. Определим его:

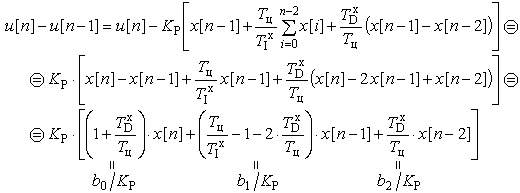(11).

Перенесем u[n-1] в правую часть - получим "скоростной" алгоритм для программной реализации регулятора:

(*)

u[n] = u[n-1] + b₀ x[n] + b₁ x[n-1] + b₂ x[n-2] (12).

Запишем РУ (*) для изображений в z-домене:

U [z] (1- z ^-1) = (b₀ + b₁ z ^-1 + b₂ z ^-1) X [z] ,

и представим его в виде дискретной ПФ:

. (13).

Анализ ее коэффициентов показывает, что:

1. Для исключения статической ошибки, ПФ должна иметь полюс z^x=1.

2. Если b₂ = 0, то получим PI-регулятор.

Если b₀ = 0, а b₁ = (1 + b₂), то получим PD-регулятор.

Синтез цифрового регулятора системы по критерию быстродействия

Импульсные системы обладают специфической особенностью: переходные процессы в них могут заканчиваться за конечное число периодов дискретности, равное порядку системы п. Условием получения конечной длительности переходного процесса является равенство всех (кроме первого) коэффициентов характеристического уравнения нулю.

При этом характеристический полином системы имеет вид

(14)

а изображение выходной величины оказывается конечным рядом отрицательных степеней z:

(15)

что соответствует переходному процессу с конечной длительностью t_ПП = пТ₀.

При любом другом соотношении коэффициентов длительность переходного процесса больше пТ₀. Поэтому процесс с конечной длительностью будет оптимальным по быстродействию.

Передаточную функцию регулятора можно рассчитать по формуле для оптимального быстродействия:

, (16)

где ,

- дискретная передаточная функция разомкнутой части объекта.