TViMS_2_laba (1)

Лабораторная работа №2

Для уровня значимости  = 0,05 проверить гипотезу о законе распределения непрерывной случайной величины, характеризующей временя отпускания якоря.

Выборка значений и статистический ряд распределения исследуемой величины представлены в примере 47.

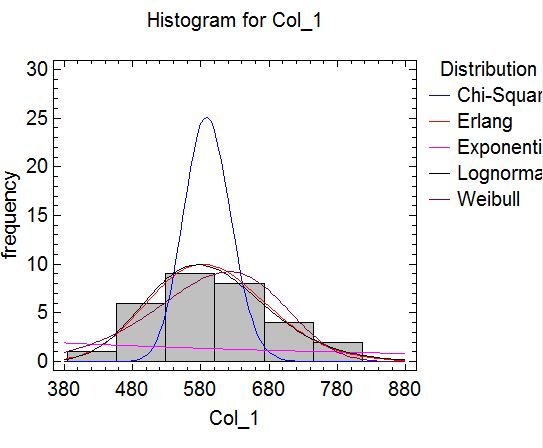
Решение. По виду гистограммы и предметной постановке задачи выдвинем гипотезу об экспоненциальном законе распределения времени отпускания якоря (см. п. 1.2.11). То есть H₀:   E(), где  – время отпускания якоря, альтернативная гипотеза состоит в том, что изучаемая величина не имеет показательного закона распределения, т. е. H_а:   E().

Найдем оценку параметра  экспоненциального распределения величины  с помощью выражения (46), определяющего связь с математическим ожиданием величины , оцененным в примере 51:

 = 595.497^–1 = 0,001679.

Исходя из предположения о показательном законе распределения величины , вычислим вероятности того, что  попадет в каждый из интервалов статистического ряда распределения (см. пример 47, таблицу 16). Для этого воспользуемся, например, свойством 5 функции распределения (см. п. 1.2.3):

;

…

Учитывая, что рассматриваемая случайная величина (время отпускания якоря) может принимать любые положительные значения, в том числе большие 816,49 мс, правую границу последнего интервала (C₆) примем равной «+».

Результаты расчетов сведем в таблицу 20.

Таблица 20–Интервальный статистический ряд величины времени между заявками с определенными вероятностями попадания значений в интервалы

Интервалы (Ci–1; Ci]	(384,61; 456,59]	(456,59; 528,57]	(528,57; 600,55]	(600,55; 672,53]	(672,53; 744,51]	(744,51; ]	Сумма
Частота (фактическая) mi	1	6	9	8	4	2	30
Вероятность pi	0,535	0,053	0,047	0,042	0,037	0,286	1
Гипотетическая частота n pi	16,064	1,587	1,406	1,246	1,104	8,593	30

Определим гипотетические частоты n p_i попадания значений случайной величины в каждый из интервалов, т.е. среднее количество попаданий при условии, что исследуемая величина действительно имеет экспоненциальное распределение. Ввиду того, что значения величины  из интервалов (456,59; 528,57]и (528,57; 600,55] : (600,55; 672,53] и (744,51;816,49]

ожидаются в выборке менее 3 раз (см. таблицу 20), объединим данные интервалы между собой. Интервальный статистический ряд распределения величины  примет вид, представленный в таблице 21.

Таблица 21 – Интервальный статистический ряд распределения времени между заявками после объединения интервалов

Интервалы (Ci–1; Ci]	(384,61; 456,59]	(456,59; 600,55	(600,55; 744,51]	(744,51; ]
Частота (фактическая) mi	1	15	12	2
Вероятность pi	0,535	0,1	0,079	0,286
Гипотетическая частота npi	16,064	3	2,35	8,593

Определим выборочное значение статистического критерия значимости ² Пирсона по выражению (146):

 .

Определим критическое значение статистического критерия значимости Пирсона , где k – количество интервалов разбиения вариационного ряда (k = 4); r – количество параметров гипотетической функции распределения (для экспоненциального закона распределения r = 1). В соответствии с таблицей Д.4:

 .

Вывод: поскольку выборочное значение критерия «согласия» больше критического ( ), т.е. не принадлежит ОДЗ, то гипотеза H₀:   E() об экспоненциальном законе распределения исследуемой величины не согласуется с результатами экспериментов.

Следовательно, есть основания считать, что закон распределения времени отпускания якоря, отличается от экспоненциального (для уровня значимости 0,05). Подобная ситуация не характерна для простейшего потока заявок (см. замечание в п. 1.5.3).  

Выполним компьютерный расчет в пакете Statgraphics (в соответствии с инструкцией). При этом в качестве возможных типовых распределений случайной величины выберем (в соответствии с предметной постановкой задачи и видом гистограммы) распределение экспоненциальное, логнормальное, Вейбулла, F-Фишера, Эрланга и хи-квадрат.

В качестве критериев согласия выбираем критерий Хи-квадрат Пирсона и критерий Колмогорова-Смирнова.

Uncensored Data - Col_1

Data variable: Col_1

30 values ranging from 420,6 to 780,5

Fitted Distributions

Chi-Squared	Erlang	Exponential	Lognormal
degrees of freedom = 590,182	shape = 47,0	mean = 595,497	mean = 595,742
	scale = 0,0789257		standard deviation = 89,1438
			Log scale: mean = 6,37874
			Log scale: std. dev. = 0,148807

Weibull

shape = 7,27391

scale = 633,641

Goodness-of-Fit Tests for Col_1

Chi-Squared Test

	Chi-Squared	Erlang	Exponential	Lognormal	Weibull
Chi-Squared	38,5005		125,076	2,00009	8,25
D.f.	5	0	11	4	7
P-Value	2,99316E-7	<	0,0	0,735741	0,311066

Kolmogorov-Smirnov Test

	Chi-Squared	Erlang	Exponential	Lognormal	Weibull
DPLUS	0,302593	0,0	0,269639	0,103548	0,127047
DMINUS	0,259461	1,0	0,506534	0,0632257	0,0813429
DN	0,302593	1,0	0,506534	0,103548	0,127047
P-Value	0,00822467	0,0	4,12326E-7	0,904562	0,718103

The StatAdvisor

This pane shows the results of tests run to determine whether Col_1 can be adequately modeled by various distributions. The chi-squared test divides the range of Col_1 into nonoverlapping intervals and compares the number of observations in each class to the number expected based on the fitted distribution. The Kolmogorov-Smirnov test computes the maximum distance between the cumulative distribution of Col_1 and the CDF of the fitted distribution. The other statistics compare the empirical distribution function to the fitted CDF in different ways.

P-values less than 0,05 would indicate that Col_1 does not come from the selected distribution with 95% confidence.

Comparison of Alternative Distributions

Distribution	Est. Parameters	Log Likelihood	KS D
Birnbaum-Saunders	2	-176,257	0,105847
Inverse Gaussian	2	-176,257	0,105775
Gamma	2	-176,262	0,113221
Erlang	2	-176,262	1,0
Lognormal	2	-176,277	0,103548
Normal	2	-176,525	0,122788
Uniform	2	-176,575	0,133389
Loglogistic	2	-176,91	0,115856
Largest Extreme Value	2	-177,047	0,077752
Logistic	2	-177,162	0,123215
Weibull	2	-177,708	0,127047
Laplace	2	-178,984	0,125947
Smallest Extreme Value	2	-179,397	0,127534
Exponential	1	-221,682	0,506534
Chi-Squared	1	-228,358	0,302593
Pareto	1	-276,951	0,612159

The StatAdvisor

This table compares the goodness-of-fit when various distributions are fit to Col_1. You can select other distributions using Pane Options.

According to the log likelihood statistic, the best fitting distribution is the Birnbaum-Saunders distribution. To fit this distribution, press the alternate mouse button and select Analysis Options.

Вывод по компьютерному расчету: проведя компьютерный расчет в пакете Statgraphics, мы выяснили, что для проверяемой гипотезы об экспоненциальном распределении не выполняется неравенство P-Value  (0,0   0,05), следовательно, для уровня значимости = 0,05 данная гипотеза не согласуется с экспериментальными данными (основания для отклонения гипотезы есть).

Кроме того, мы выяснили, что логнормальное распределение (P-Value = 0,735741) лучше аппроксимирует экспериментальные данные, чем распределение Вейбулла (P-Value = 0,311066), экспоненциальное распределение (P-Value = 0,0) и распределение Хи-квадрат (P-Value = 2,99316E-7).

Итоговый вывод: проверка гипотезы об экспоненциальном распределении в ручном и компьютерном расчете показала неаналогичные результаты (гипотеза не согласуется). Различия в ручном и машинном расчетах связаны с различиями в построении статистического закона распределения и способа объединения интервалов.