2. Расчет с помощью функции линейн с расшифровкой полученных результатов;

1.2.1 Параметры линейной регрессии

можно определить с помощью встроенной статистической функции ЛИНЕЙН MS Excel. Порядок вычисления следующий:

1) ввожу исходные данные (рисунок 1).

2) выделяю область пустых ячеек 52 (5 строк, 2 столбца) с целью вывода результатов регрессионной статистики или область 12 – для получения только оценок коэффициентов регрессии;

3) активизирую Мастер функций любым из способов:

а) в главном меню выбираю Вставка / Функция;

б) на панели инструментов Стандартная щелкаю по кнопке Вставка функции;

4) в окне «Категория» выбераю Статистические, в окне «Функция» – ЛИНЕЙН. Щелкаю по кнопке ОК (рисунок 2);

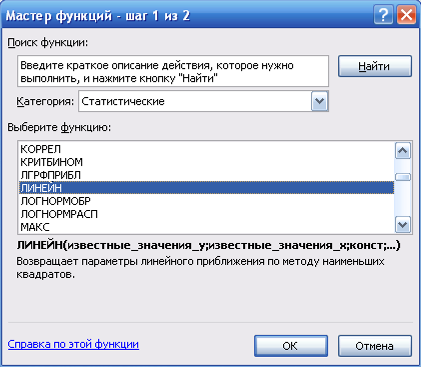
Рисунок 2 Диалоговое окно Мастер функций

5) заполняю аргументы функции (рисунок 3):

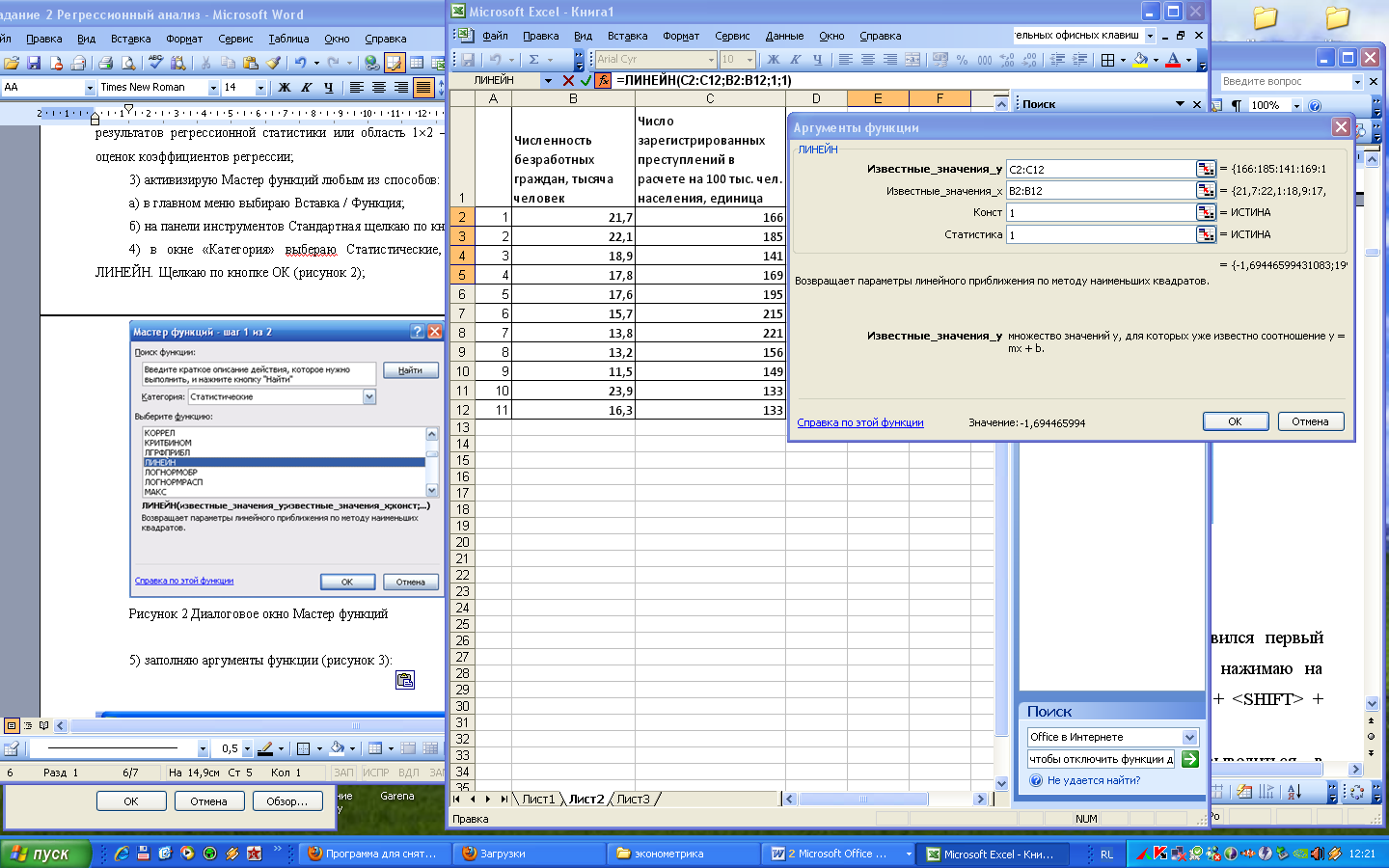
Рисунок 3 Диалоговое окно Аргументы функции

Щелкаю по кнопке ОК;

6) в левой верхней ячейке выделенной области появился первый элемент итоговой таблицы.

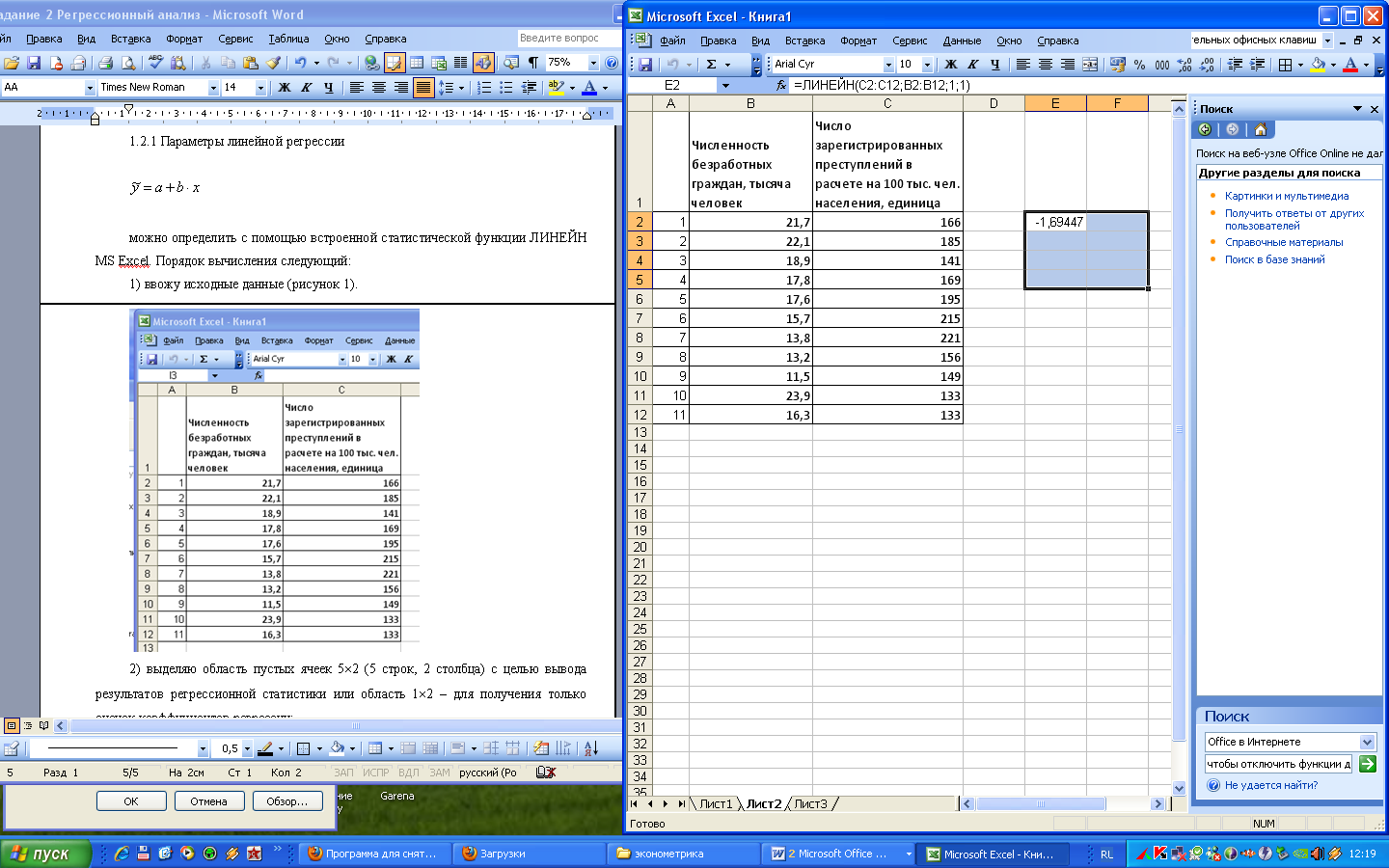
Чтобы раскрыть всю таблицу, нажимаю на клавишу <F2>, а затем – на комбинацию клавиш <CTRL> + <SHIFT> + <ENTER>.

Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Коэффициент детерминации R2	Среднеквадратическое отклонение y
F – статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Результаты вычислений функции ЛИНЕЙН представлены на рисунке 4.

Рисунок 4 Результаты вычислений функции ЛИНЕЙН

2. графическое построение линии тренда;

x	y
11,5	149
13,2	156
13,8	221
15,7	215
16,3	133
17,6	195
17,8	169
18,9	141
21,7	166
22,1	185
23,9	133

Построим график этой зависимости (можно График, можно Точечная)

Есть несколько базовых функций (линейная, логарифм, экспонента, полиномы,…). Если у нас есть неизвестно какая зависимость, Excel может нам сказать, на какую базовую функцию она похожа больше всего.

Для этого поступим так. Построим график этой зависимости (можно График, можно Точечная), воспользуемся пунктом Меню=>Диаграмма=>Добавить линию тренда. Выберем тип тренда. Excel построит на диаграмме еще один график, показывающий, к какой зависимости ближе всего исследуемые данные.

Например, если мы выберем тип тренда “Линейная”, то Excel построит линейную функцию, которая лучше всего описывает исследуемую зависимость. На диаграмме это будет выглядеть так: это будет такая прямая линия, что график построенной функции отклоняется от нее наименьшим образом.

Примечание: Excel использует метод наименьших квадратов. Т.е. Excel строит тренд с условием, что сумма квадратов расстояний от реальных точек до линии тренда минимальна для всех линий данного типа.

Как понять, что за тренд построен? Очень просто. Надо вывести его уравнение (“Формат линии тренда”, вкладка “Параметры”, соответствующая галка). И вы узнаете приблизительное уравнение зависимости между вашими данными.

Как понять, какой тип тренда надо использовать? На той же вкладке “параметры” окна “формат линии тренда” включаем галку “поместить на диаграмму величину достоверности аппроксимации (R^2)”. После этого в подписи к тренду появится эта самая величина достоверности. Чем она больше, тем лучше построенный тренд.

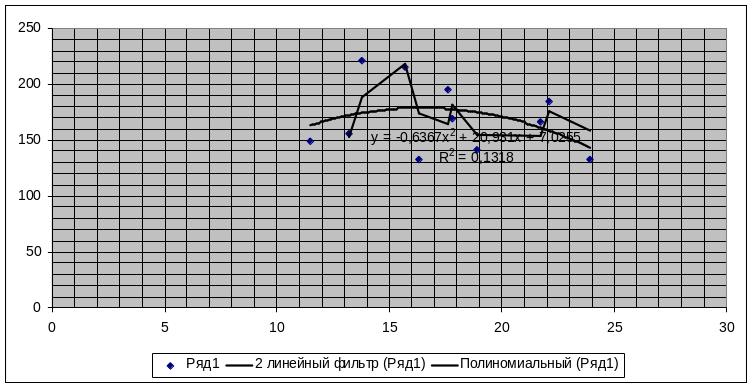
Получаем тип тренда полиномиальная аппроксимация со степенью 2

Y= -0,6367x² +20,931х+7,0255

R²=0,1318