1.2 Определить коэффициенты корреляции;

Выборочный коэффициент корреляции

=-0,21393

Данный коэффициент корреляции характеризует низкую тесноту связи

=-1,69447*(-1,69447)*154,68/9704,545= 0,045764

коэффициент детерминации, по модулю меньше 1 и чем ближе к 0, тем меньше рассеяние, от прогнозируемой связи.

Это значит, что 4% вариации "у" объясняется вариацией фактор "х".

1.3 Оценить статистическую надежность и значимость вычисленных коэффициентов корреляции

Определение статистической значимости уравнения регрессии с помощью F-критерия Фишера

Определим F- критерий Фишера:

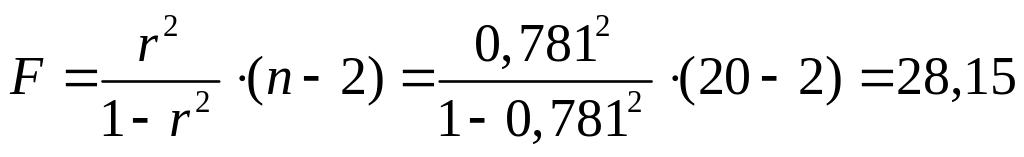
₌ 0,43163

Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы 1 и (11-2)=9 составляет Fтаб = 5,12.

Имеем F< Fтаб, следовательно уравнение регрессии не значимо, статистически не надежно.

Оценка статистической значимости параметров регрессии с помощью t-статистики Стьюдента

Табличное значение t-критерия для числа степеней свободы df=n-2=11-2=9 и уровня значимости α=0,05 составит t_табл=2,2622.

Определим стандартные ошибки:

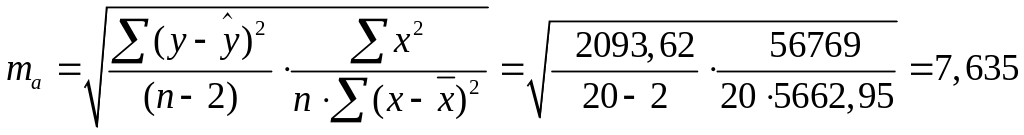46,15977

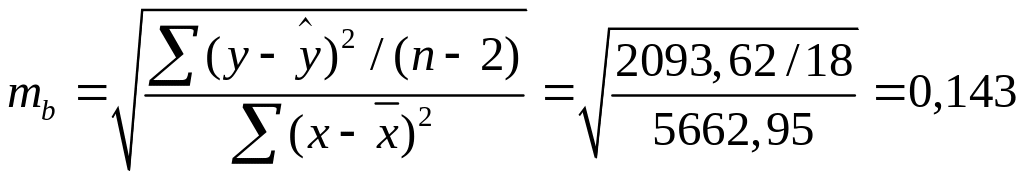2,579153

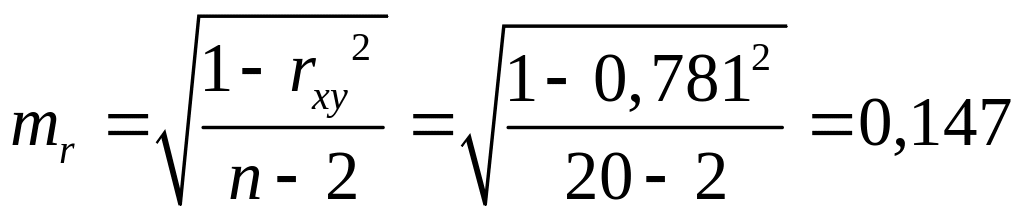0,325617

Тогда

4,311477

-0,65699

-0,65699

Фактические значения t-статистики превосходят табличное значение:

t_a>t_tab, t_b< t_tab, t_r< t_tab поэтому параметр а статистически значим, а b, и rxy статистически не значимы.

Рассчитаем доверительные интервалы для параметров регрессии а и b. Для этого определим предельную ошибку для каждого показателя:

104,4226

5,83456

Получаем доверительные интервалы:

199,02±104,4226 и 94,59≤а≤303,44

-1,69±5,83456 и -7,53≤b≤4,14

Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью р=1-α=1-0,05=0,95 параметры а и b, находятся в указанных границах, не принимают нулевых значений, т.е. являются статистически значимыми и существенно отличны от нуля.

Задание 2 Регрессионный анализ

2. По исходным данным выполнить регрессионный анализ:

   1. Рассчитать параметры уравнения линейной парной регрессии для чего использовать:

      1. расчет в Excel по формулам, реализующим метод наименьших квадратов;

      2. расчет с помощью функции ЛИНЕЙН с расшифровкой полученных результатов;

      3. графическое построения линии тренда;

      4. инструмент «Регрессия».

   2. Оценить статистическую надежность результатов регрессионного моделирования для чего построить доверительные интервалы коэффициентов регрессии по t-критерию Стьюдента

   3. Оценить статистическую значимости коэффициентов регрессии и всего уравнения регрессии с помощью t-критерия Стъюдента и F-критерия Фишера.

   4. Оценить качество уравнения регрессии с помощью средней ошибки аппроксимации.

   5. Дать с помощью общего (среднего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.

   6. Сделать итоговые выводы.

Численность безработных граждан, тысяча человек	Число заpегистpиpованных пpеступлений в pасчете на 100 тыс. чел. населения, единица
21,7	166
22,1	185
18,9	141
17,8	169
17,6	195
15,7	215
13,8	221
13,2	156
11,5	149
23,9	133
16,3	133