Амплитудная модуляция.

АМ- сигналы получают в следующем преобразовании. Пусть исходный сигнал u(t). С помощью амплитудного модулятора формируют сигнал: u_AM(t)=[U_m+u(t)]cos(ω₀t).       (7.1)

  Наглядный образ АМ-сигнала легко представить в случае, когда исходный, т.е. модулирующий сигнал гармоническийu(t)= U_Мcos(Ωt)

 На рис.7.1 приведена функциональная схема АМ - модулятора.

 Рис.7.1. demo7_1

         В этой схеме модуляцию производит модулятор – умножитель сигналов K*XY. K – постоянный коэффициент, равный 1.X-  1-ый сомножитель в выражении (7.1), сумма напряжений источников V1 и V2. V1 – источник синусоидального напряжения с амплитудой U_М=1В и частотой  F= 50Гц  (Ω = 2πF).V2 - источник постоянного напряженияU_m=5В. Y- 2-ой сомножитель в выражении (7.1), напряжение источника V3. V3 – источник синусоидального напряжения с амплитудой U_М=1В и частотой  f= 2кГц  (ω₀ = 2πf).

На рис.7.2. показаны осциллограммы модулирующего u(t) в узле 4  (зеленая линия) и модулированного u_AM(t) в узле 3 (синяя линия) сигналов, а также «несущего» полезный сигнал гармонического колебания в узле 2 (красная линия).

 

Рис.7.2. Амплитудная модуляция.

 Видно, что амплитуда АМ-колебания изменяется синхронно с изменениями модулирующего колебания. Количественным параметром АМ-колебания является коэффициент модуляции, который не должен быть больше 1:

m =(Umax - Umin)/(Umax + Umin)=(75-50)/(75+50)=25/125=0.2

 Если разложить в ряд Фурье АМ-колебание, то получится его спектр (набор гармонических составляющих:

 u_AM(t)=[U_m+u(t)]cos(ω₀t)= U_mcos(ω₀t)+ U_Мcos(Ωt)cos(ω₀t)=

= U_mcos(ω₀t)+U_М/2cos(ω₀+Ω)t+ U_М/2cos(ω₀-Ω)t= =U_mcos(ω₀t)+mU_m/2cos(ω₀+Ω)t+ mU_m/2cos(ω₀-Ω)t.

 На рис. 7.3 показана спектральная диаграмма для АМ-колебания для рассмотренного случая гармонической модуляции.

Рис.7.3.

 Спектральная диаграмма показывает диапазон частот, занятый АМ – сигналом. Если исходный сигнал представляется рядом Фурье, т.е. набором гармонических составляющих из k гармоник с первой гармоникой Ω₀, то диапазон частот, соответственно, составит от (ω₀-k Ω₀) до (ω₀+k Ω₀). Такую же полосу пропускания должен иметь канал связи, по которому передается АМ-сигнал. Для уменьшения полосы иногда используют только часть спектра меньше  или больше ω₀, т.к. в полном спектре информация повторяется.

Частотная модуляция.

В ЧМ-сигнале по закону управляющего напряжения изменяется частота сигнала:

u_ЧM(t) = U_mcos[ω₀+k u(t)]t.

 Пример ЧМ-сигнала при гармонической модуляции

u_ЧM(t) = U_mcos[ω₀ +msin(Ω t)]t

 приведен на рис.7.4.

 Фазовая модуляция.

В ФМ-сигнале функцией модулирующего сигнала является фаза модулированного колебания.  Поскольку частота и фаза связаны как интеграл или производная, то они схожи по свойствам. Поэтому в теории ЧМ- и ФМ-сигналы объединены понятием угловая модуляция.         Полоса частот, занимаемая сигналом с угловой модуляцией, зависит от индекса модуляции M= Δω/Ω и достигает 2(M+1)Ω. Если M >> 1 (широкополосная модуляция), то диапазон частот, занимаемый ЧМ-сигналом в M раз больше, чем диапазон частот АМ-сигнала. Поэтому ЧМ–сигнал можно полезно реализовать только на частотах более сотен мегагерц.

 

 

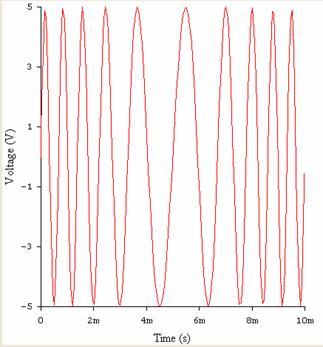
Рис.7.4.demo7_2.

ФМ- сигнал в отличие от ЧМ-сигнала имеет своим недостатком зависимость ширины спектра от индекса модуляции. Поэтом практически всюду используется ЧМ-сигнал.

Отличительной особенностью ЧМ-сигнала является его высокая помехозащищенность.

5. Общее понятие о помехах. Виды помех: случайные и детерминированные,  внешние и внутренние, аддитивные и мультипликативные, естественные и искусственные. Классификация помех по видам связей с источником помех.