Федеральное агентство железнодорожного транспорта

Уральский государственный университет путей сообщения

Кафедра прикладной математики

Кафедра высшей математики

Элементы математической статистики

Екатеринбург

2005

Федеральное агентство железнодорожного транспорта

Уральский государственный университет путей сообщения

Кафедра прикладной математики

Кафедра высшей математики

Элементы математической статистики

Учебно-методическое пособие

для студентов второго и третьего курсов

различных специальностей технических вузов

Екатеринбург

2005

Учебно-методическое пособие предназначено для выполнения курсовой работы по математической статистике или лабораторных работ по трем темам: выбор теоретического вида распределения, однофакторный анализ, регрессионный анализ. Методическое пособие содержит теоретическую часть, 30 заданий для выполнения лабораторной работы по каждой теме, специальные таблицы.

Предназначено для студентов второго и третьего курсов различных специальностей технических вузов.

Утверждено на заседании кафедры прикладной математики.

Авторы:

В.В. Башуров, доцент кафедры прикладной математики УрГУПС, канд. физ.– мат. наук,

О.А. Башурова, ассистент кафедры прикладной математики УрГУПС,

О.В. Куликова, доцент кафедры высшей математики УрГУПС, канд. пед. наук,

Г.А. Тимофеева, профессор кафедры высшей математики УрГУПС, доктор физ.– мат. наук.

Рецензент:

А.Н. Сесекин, зав. кафедрой прикладной математики УГТУ–УПИ, профессор, доктор физ.– мат. наук.

© Уральский государственный университет путей сообщения (УрГУПС), 2005

Оглавление

1. Выборочный метод ……………………………………………………...……….4

2. Статистические оценки параметров распределения …………………………..5

3. Доверительный интервал ………………………………………….…………….8

4. Метод моментов оценки параметров распределения ………………………....9

5. Проверка статистических гипотез ………………………………………….…10

Задача о выборе теоретического вида распределения ……………………….12

6. Однофакторный анализ ……………………………………………………...…17

Задача о влиянии фактора на случайную величину ………………………….20

7. Регрессионный анализ ………………………………………………………....23

Задача о зависимости системы случайных величин ……….……………...…26

Библиографический список..…………….……………………………………..29

Приложение 1. Таблица «Критические точки распределения » …………30

Приложение 2. Таблица «Критические точки распределения Стьюдента»...31

Приложение 3. Таблица «Критические точки распределения Фишера».…...32

Задание 1 ……….………..…………………………………..………………….33

Задание 2 ……….………………………..…………………..………………….63

Задание 3 ………….…………………………………………………………….70

Математическая статистика – одно из направлений прикладной математики, занимающееся обработкой данных наблюдений и экспериментов с целью изучения объективно существующих закономерностей и взаимосвязей.

1. Выборочный метод

Пусть необходимо изучить совокупность однородных объектов относительно некоторого признака, характеризующего эти объекты. Данная совокупность называется генеральной совокупностью. Если число объектов (объем) генеральной совокупности достаточно большое, то из нее случайным образом выбираем ограниченное число объектов для изучения, называемое выборочной совокупностью или выборкой.

Пусть произведена выборка объема из генеральной совокупности, причем значение наблюдалось раз, значение – раз,…, значение – раз ( ). Результаты наблюдений записываем в таблицу, называемую статистическим рядом (распределением) выборки:

			…
			…
			…

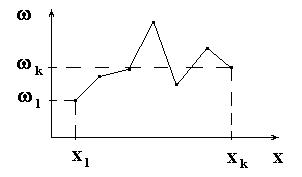В таблице называются вариантами, – частотами наблюдений, – относительными частотами наблюдений, – числом разрядов. Для иллюстрации статистического ряда строим полигон относительных частот – ломанная, последовательно соединяющая точки .

В случае изучения непрерывно распределенного признака объектов выборки строим интервальный статистический ряд (распределение) выборки

			…
			…
			…

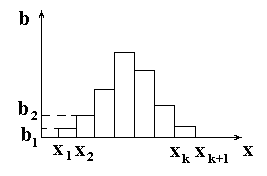Здесь диапазон наблюдений разбиваем на интервалы (желательно одинаковой длины ), а – число наблюдений, попавших в соответствующий интервал. В качестве иллюстрации рисуем гистограмму – ступенчатая фигура, состоящая из прямоугольников с основаниями и высотами .