4. Бифуркации смены устойчивости периодических движений.

Важной характеристикой бифуркаций смены устойчивости периодических движений являются значения мультипликаторов в критический момент, которые представляют собой коэффициенты усиления (затухания) малых возмущений на фоне рассматриваемого периодического движения за период T.

Математически мультипликаторы – это собственные значения матрицы expRT, характеризующей решение Z(t)=C(T)·expRT линеаризованной системы в окрестности исследуемого периодического движения x=f(t, m), f(t+T, m)ºf(t, m). Здесь R постоянная, С(t) – периодическая матрица: С(t+T)ºС(t).

В автономной системе, описываемой уравнениями, явно независящими от времени, один из мультипликаторов всегда равен единице, поэтому в дальнейшем говорится только об остальных. Если все остальные мультипликаторы по модулю меньше 1, то исходное периодическое движение устойчиво. Бифуркации, связанные с потерей устойчивости, происходят при значениях параметров системы, при которых один или несколько из них равны по модулю 1. В случае равенства одного из мультипликаторов единице осуществляется так называемая бифуркация удвоения периода (табл., строка 1). Она характеризуется тем, что в момент бифуркации (его называют точкой бифуркации) малое по модулю возмущение через период просто меняет знак, а через следующий оборот в линейном приближении происходит замыкание траектории. В результате этой бифуркации из исходного периодического движения рождается устойчивое периодическое движение приблизительно удвоенного периода, а исходный режим становится неустойчивым.

Б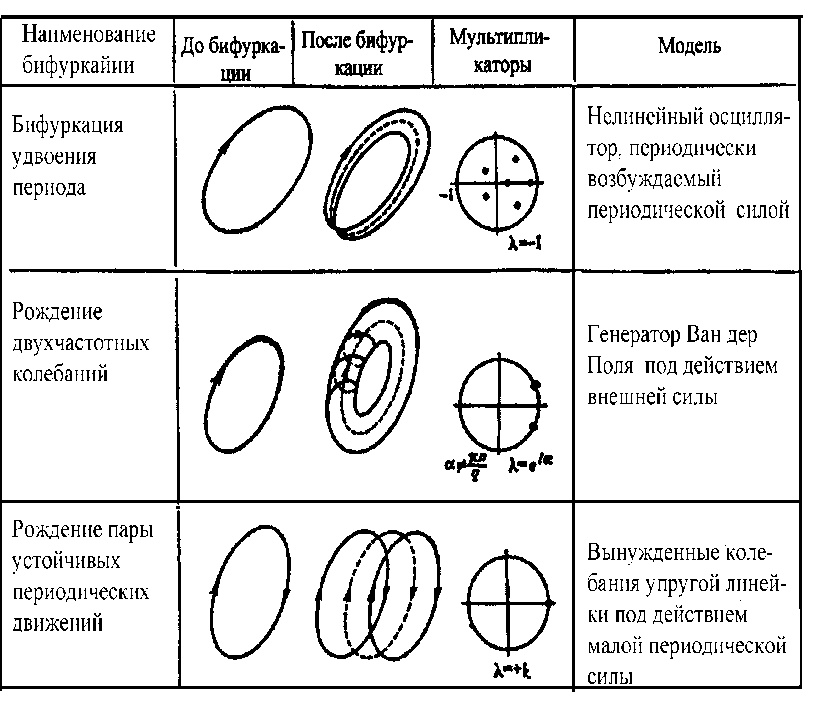 есконечная цепочка бифуркаций удвоения периода – один из наиболее распространенных путей возникновения стохастического поведения в реальных системам. Появлению двухчастотных колебаний в физической системе отвечает бифуркация рождения двумерного тора из периодической траектории (табл. , строка 2).

В системах, зависящих от двух параметров, или в системах с определенным типом симметрии встречается бифуркация, при которой рождается сразу 2 устойчивых предельных цикла (табл., строка 3). Такая бифуркация характерна для нелинейных систем, в которых зависимость потенциальной энергии от переменной имеет два минимума, находящихся под действием внешних сил.

5. Заключение. Важные черты бифуркации

Бифуркации, в результате которых исчезают статические или периодические режимы (то есть состояния равновесия или предельные циклы), могут приводить к тому, что динамическая система переходит в режим стохастических колебаний.

В приложениях теории бифуркаций ставится задача – для каждой конкретной ситуации найти аналитические выражения для вариантов решений уравнений, возникающих в точках бифуркации, а также определение значений параметров, при которых начинается ветвление решений уравнений. Предварительно необходимо провести анализ устойчивости системы и поиск точек ее неустойчивости. Методы этого анализа основаны на теории устойчивости, они достаточно подробно разработаны и носят чисто технический характер.

В теории бифуркаций описано большое число бифуркационных ситуаций. В развитии реальных природных систем могут наблюдаться не отдельные бифуркации, а целые каскады бифуркаций (классическим примером может служить возникновение турбулентности и других гидродинамических неустойчивостей). Кроме того, различают бифуркации и катастрофы. Существует даже теория катастроф. Однако, анализ связей и различий между ними выходит за пределы данного учебного пособия.

Очень важная черта бифуркаций: В момент времени, когда система находится вблизи точки бифуркации, огромную роль начинают играть малые возмущения значений ее параметров. Эти возмущения могут носить как чисто случайный характер, так и быть целенаправленными. Именно от них зависит, по какой эволюционной ветви пойдет система, пройдя через точку бифуркации. То есть, если до прохождения точки бифуркации, поведение системы подчиняется детерминистским закономерностям, то в самой точке бифуркации решающую роль играет случай.

Вследствие этого, по словам И. Пригожина, мир становится «загадочным, непредсказуемым, неконтролируемым». В определенном отношении это так. Но полностью с этим высказыванием нельзя согласиться, поскольку для любой системы в точке бифуркации имеется не произвольный, а вполне определенный набор путей эволюции. Поэтому даже если работает случайность, то она работает в строго определенном поле возможностей. И, следовательно, говорить о полной неопределенности и, тем более, полной загадочности некорректно. Что же касается неконтролируемости, то, конечно, говорить о тотальном контроле не имеет смысла, но в некоторых процессах возможно вмешательство как подталкивание к желаемым вариантам развития.