Министерство науки и образования Украины

Харьковский национальный университет имени В.Н. Каразина

Факультет компьютерных наук

Кафедра теоретической и прикладной системотехники

Курсовая работа по дисциплине:

«Современные сетевые технологии»

на тему:

«Теория Бифуркаций»

Выполнила:

Студентка 5 курса

Группы КСУ-51

Ускова А.И.

Харьков – 2013

Учебные вопросы:

1. Основные понятия и определения теории бифуркаций. 3

а) Введение в теорию бифуркаций 3

б) Понятие бифуркационной диаграммы 5

в) Точка бифуркации и свойства точки бифуркации 5

г) Понятие аттрактора 7

2. Бифуркации состояний равновесия. 8

а) Слияние и последующее исчезновение двух состояний равновесия. 8

б) Рождение предельного цикла из состояния равновесия. 9

в) Рождение из одного равновесного состояния трёх состояний равновесия (спонтанное нарушение симметрии). 9

3. Бифуркации рождения периодического движения. 10

4. Бифуркации смены устойчивости периодических движений. 11

5. Заключение. Важные черты бифуркации 12

6. Список используемой литературы 14

1. Основные понятия и определения теории бифуркаций.

а) Введение в теорию бифуркаций

Теория бифуркаций динамических систем описывает качественные, скачкообразные изменения фазовых портретов дифференциальных уравнений при непрерывном, плавном изменении параметров. Так, при потере устойчивости особой точкой может возникнуть предельный цикл, а при потере устойчивости предельным циклом – хаос. Такого рода изменения и называются бифуркациями.

В дифференциальных уравнениях, описывающих реальные физические явления, чаще всего встречаются особые точки и предельные циклы общего положения, то есть гиперболические. Однако встречаются и специальные классы дифференциальных уравнений, где дело обстоит иначе. Таковы, например, системы, обладающие симметриями, связанными с природой описываемого явления, а также гамильтоновы уравнения, обратимые системы, уравнения, сохраняющие фазовый объем. Так, например, рассмотрим однопараметрическое семейство динамических систем на прямой с симметрией второго порядка:

Т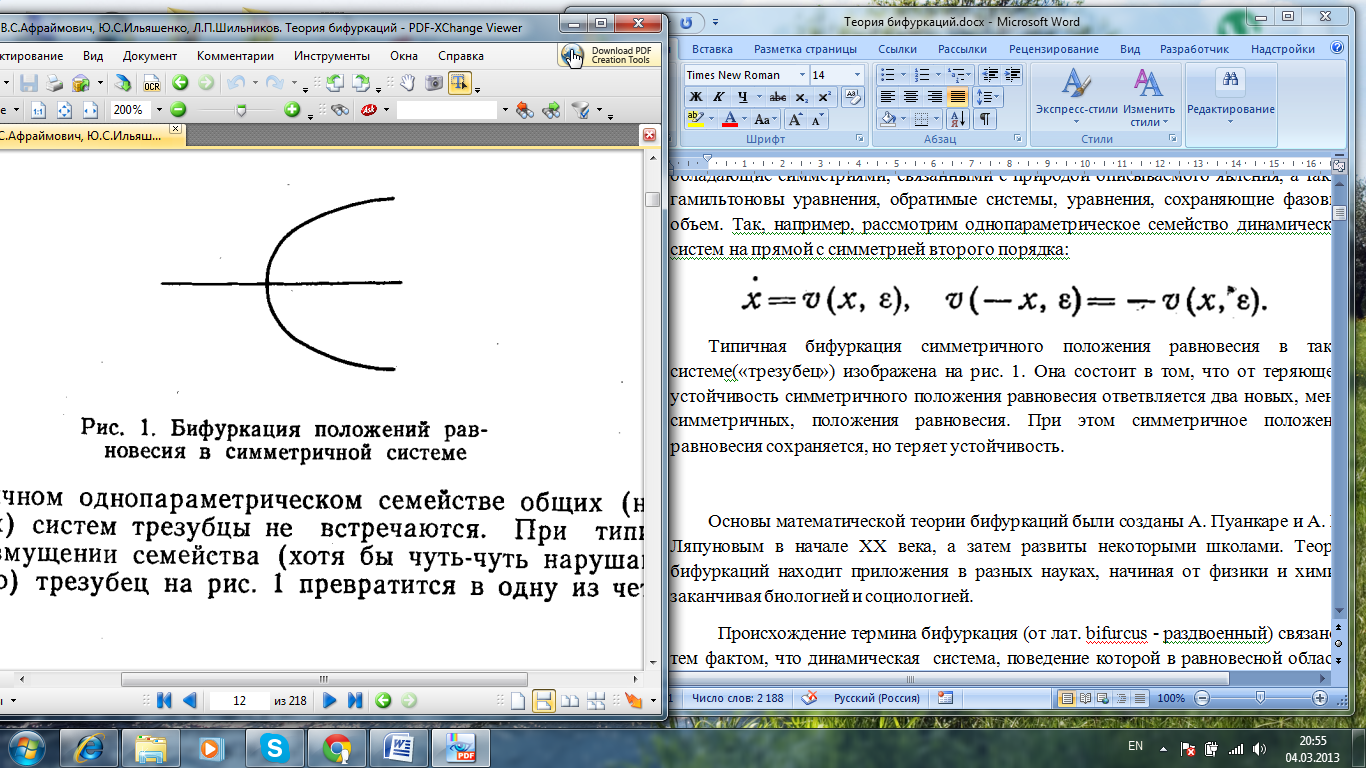 ипичная бифуркация симметричного положения равновесия в такой системе(«трезубец») изображена на рис. 1. Она состоит в том, что от теряющего устойчивость симметричного положения равновесия ответвляется два новых, менее симметричных, положения равновесия. При этом симметричное положение равновесия сохраняется, но теряет устойчивость.

Основы математической теории бифуркаций были созданы А. Пуанкаре и A. M. Ляпуновым в начале ХХ века, а затем развиты некоторыми школами. Теория бифуркаций находит приложения в разных науках, начиная от физики и химии, заканчивая биологией и социологией.

Происхождение термина бифуркация (от лат. bifurcus - раздвоенный) связано с тем фактом, что динамическая система, поведение которой в равновесной области описывается системой линейных дифференциальных уравнений, имеющих единственное решение, при изменении параметров до некоторого критического значения, достигает так называемой точки бифуркации – точки ветвления возможных путей эволюции системы.

Этот момент (точка ветвления) соответствует переходу системы в неравновесное состояние, а на уровне математического описания ему соответствует переход к нелинейным дифференциальным уравнениям и ветвление их решений.

Бифуркацией называется приобретение нового качества эволюции (в движении) динамической системы при малом изменении ее параметров. Бифуркация соответствует перестройке характера движения или структуры реальной системы (физической, химической, биологической и т. д.).

С позиций математики, бифуркация – это смена топологической структуры разбиения фазового пространства динамической системы на траектории при малом изменении ее параметров.

Это определение опирается на понятие топологической эквивалентности динамических систем: две системы топологически эквивалентны, если они имеют одинаковую структуру разбиения фазового пространства на траектории, если движения одной из них могут быть сведены к движениям другой непрерывной заменой координат и времени.

П римером такой эквивалентности служат движения маятника при разных величинах коэффициента трения k: при малом трении траектории на фазовой плоскости имеют вид скручивающихся спиралей, а при большом – парабол (рис. на следующем слайде)

Переход от фазового портрета а к б не представляет собой бифуркации, поскольку бифуркации – это переход от данной системы к топологически неэквивалентной.

П

Фазовые портреты маятника при разных k: а – k< 2; б–k >2

ример: В математической модели возникновению ячеек Бенара соответствует бифуркация рождения новых состояний равновесия (соответствующих ячеистой структуре).

Среди различных бифуркаций при анализе моделей физических систем особенно интересны, так называемые, локальные – это бифуркации, при которых происходит перестройка отдельных движений динамической системы.

Простейшими и наиболее важными из них являются:

• бифуркации состояний равновесия (ячейки Бенара)

• бифуркации периодических движений.

б) Понятие бифуркационной диаграммы

Центральным понятием теории бифуркации является понятие (не)грубой системы. Берётся какая-либо динамическая система и рассматривается такое (много)параметрическое семейство динамических систем, что исходная система получается в качестве частного случая — при каком-либо одном значении параметра (параметров). Если при значении параметров, достаточно близких к данному, сохраняется качественная картина разбиения фазового пространства на траектории, то такая система называется грубой. В противном случае, если такой окрестности не существует, то система называется негрубой.

Основные методы теории бифуркаций — это методы теории возмущений. В частности, применяется метод малого параметра.

Таким образом в пространстве параметров возникают области грубых систем, которые разделяются поверхностями, состоящими из негрубых систем. Теория бифуркаций изучает зависимость качественной картины при непрерывном изменении параметра вдоль некоторой кривой. Схема, по которой происходит изменение качественной картины называется бифуркационной диаграммой.

В математике, особенно при изучении динамических систем, под понятием бифуркационная диаграмма подразумевают изображение на рисунке смены возможных динамических режимов системы (равновесных состояний, стационарных точек, периодических орбит и пр.) при изменении значения бифуркационного параметра.

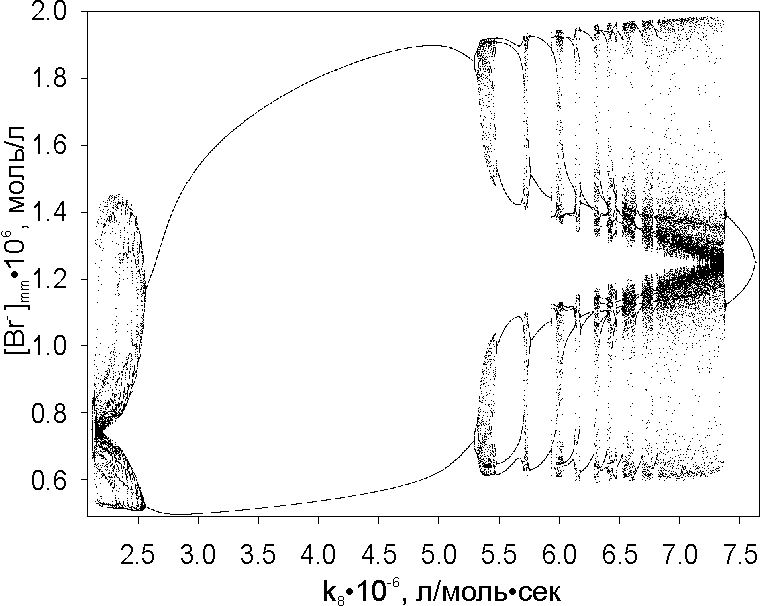
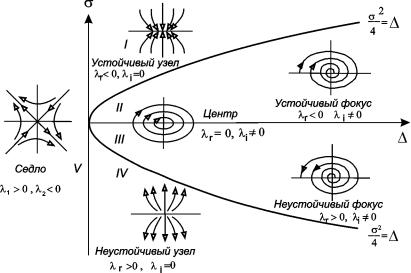
в) Точка бифуркации и свойства точки бифуркации

Точка бифуркации — в общем случае момент времени или точка места, в котором происходит непрогнозируемый переход системы в одно из иных, топологически неэквивалентных исходному, состояний. Критическое фазовое состояние системы, при котором система становится неустойчивой относительно флуктуаций (возмущений) и возникает неопределенность: станет ли состояние системы хаотическим или она перейдет в то или иное новое устойчивое состояние, например, на более дифференцированный и высокий уровень упорядоченности.

Точка бифуркации математически описывается следующим образом:

В системе x′ = f(x, ε) точкой локальной бифуркации динамической системы со стационарной точкой x₀ является точка ε = 0, если найдутся сколь угодно малые значения ε, при которых динамическая система в окрестности точки x₀ не является локально топологически эквивалентной системе, отвечающей нулевому значению параметра.

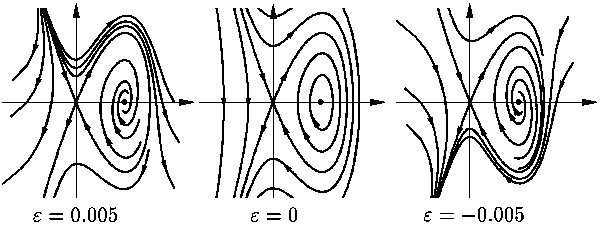
Математически описаны также бифуркация седло-узла, бифуркация гомоклинической траектории седла или бифуркация петли сепаратрисы седла, бифуркация цикла или бифуркация Пуанкаре—Андронова—Хопфа и ее частные случаи - бифуркация удвоения периода и бифуркация рождения инвариантного тора, когда вокруг потерявшего устойчивость цикла образуется инвариантное многообразие, гомеоморфное тору. В общем случае на этом торе при приближении параметра к нулевому (бифуркационному) значению в бесконечном числе рождаются и умирают длиннопериодические предельные циклы.

Для математического описания прохождения точки бифуркации используются системы дифференциальных уравнений.

Свойства точки бифуркации:

• Непрогнозируемость. Обычно точка бифуркации предваряет несколько ветвей аттрактора (устойчивых состояний системы), в одно из которых перейдет система. Однако заранее невозможно предсказать, какой новый аттрактор займёт система. Это связано с природой времени - невозможно так синхронизировать внутренние состояния элементов системы, чтобы достоверно определить, в каких состояниях они будут в момент, когда система достигнет точки бифуркации.

• Точка бифуркации носит как правило кратковременный локальный характер относительно разделямых ею более длительных устойчивых состояний системы.

На основании свойства непрогнозируемости точки бифуркации все события делятся на

• рациональные,

• иррациональные хаотические - имеющие область бифуркаций и область рациональных аттракторов, и

• иррациональные случайные - когда зона бифуркации охватывает все пространство возможных событий.

Для бифуркации рождения цикла возможно как мягкое возбуждение автоколебаний системы, сопровождающее потерю устойчивости стационарной точки системы, так и жесткое, когда фазовая точка, находившаяся в окрестности устойчивого начала координат, быстро "выбрасывается" из окрестности стационарной точки, например в окрестность имеющейся у системы удаленной устойчивой стационарной точки или удаленного устойчивого цикла.

г) Понятие аттрактора

Аттра́ктор (англ. Attract — привлекать, притягивать) — компактное подмножество фазового пространства динамической системы, все траектории из некоторой окрестности которого стремятся к нему при времени, стремящемся к бесконечности. Аттрактором может являться притягивающая неподвижная точка (к примеру, в задаче о маятнике с трением о воздух), периодическая траектория (пример — самовозбуждающиеся колебания в контуре с положительной обратной связью), или некоторая ограниченная область с неустойчивыми траекториями внутри (как у странного аттрактора).

При этом, каковы бы не были начальные значения переменных системы, по мере развития динамического процесса, они будут стремиться к одним и тем же значениям или множествам значений – аттракторам. То есть, аттракторы – это геометрические структуры, характеризующие поведение системы в фазовом пространстве по прошествии длительного времени.

Область, откуда траектории стремятся к аттрактору, называют областью притяжения аттрактора или бассейном притяжения.

Таким образом, поведение динамической системы можно разделить на два этапа: переходное поведение, пока траектория стремится к аттрактору, и асимптотическое, когда траектория находится на самом аттракторе или настолько близко к нему, что расстоянием можно пренебречь. Поскольку переходное поведение временно, а асимптотическое длится бесконечно долго, внимание исследователей обычно сосредоточено именно на последнем. Отметим, что данное описание относится к диссипативными системам. У консервативных систем нет деления на переходное и асимптотическое поведение, судьба системы при этом определяется начальными данными.

Если в фазовом пространстве имеется несколько аттракторов, то их области притяжения разделены неустойчивыми множествами точек, называемых репеллерами, от которых все или почти все соседние фазовые траектории отталкиваются.

Простейшими примерами аттракторов являются: устойчивая особая точка, устойчивый периодический режим и устойчивый тор. Простейшими примерами репеллеров являются неустойчивая особая точка, неустойчивый периодический режим и неустойчивый тор. Но они могут быть и более сложными.

В системах с размерностью фазового пространстве не меньше трех могут возникать более сложные непериодические режимы поведения и соответствующие им так называемые странные аттракторы. Степень сложности аттрактора и поведения системы может нарастать в двух направлениях.

В о-первых, может увеличиваться число независимых частот, и траектория может регулярно заполнять 3-тор, 4-тор и т.д. Во-вторых, может возникнуть режим, получивший название динамического хаоса (рис. ниже), который описывается странным аттрактором. На вид режим не является строго детерминированным, хотя и совершенно случайным его не назовешь. Траектория в этом случае никакой гладкой гиперповерхности в фазовом пространстве не заполняет, аттрактор оказывается как бы «дырявым», в отличие от тора. Сложность хаотических режимов тоже может быть различной.