§ 5. Поляризация света при двойном лучепреломлении

 

Хаотическая ориентация светового вектора в естественном свете (рис. 3.2, а) сохраняется при его распространении в изотропной среде. При наличии анизотропии – зависимости физических свойств от направления – условия распространения для волн с различной ориентацией вектора   становятся неодинаковыми. Это может привести к двойному лучепреломлению.

Двойным лучепреломлением называют явление разделения естественного света на два излучения с взаимно ортогональными линейными поляризациями.

Анизотропия наиболее ярко выражена в кристаллах, не имеющих центра симметрии. В таких кристаллах имеется одно или два направления, в которых двойное лучепреломление не наблюдается. Такие направления называют оптическими осями. Плоскость, проходящая через оптическую ось кристалла и содержащая падающий луч света, называется главным сечением.

При освещении одноосного кристалла пучком естественного света под углом к оптической оси он распадается на два линейно поляризованных луча, идущих по разным направлениям. На выходе из кристалла эти два луча распространяются параллельно первоначальному направлению. Луч с вектором  , располагающимся в плоскости главного сечения, называют необыкновенным е, а луч с вектором  , перпендикулярным плоскости главного сечения – обыкновенным о.

Показатель преломления, а, следовательно, и скорость распространения для обыкновенного луча n_o не зависит от направления в кристалле. Обыкновенный луч распространяется в кристалле по обычным законам геометрической оптики.

Для необыкновенного луча показатель преломления изменяется от n_o в направлении оптической оси до n_e в перпендикулярном к ней направлении. Если n_e > n_o, то кристаллы называют положительными, при обратном соотношении n_e < n_o – отрицательными. Зависимости показателей преломления от направления в одноосных кристаллах можно представить в виде кривых, описываемых концом вектора, направление которого совпадает с направлением луча в кристалле, а величина соответствует показателю преломления (рис. 3.5). Волновой поверхностью обыкновенного луча является сфера, волновой поверхностью необыкновенного луча – эллипсоид вращения.

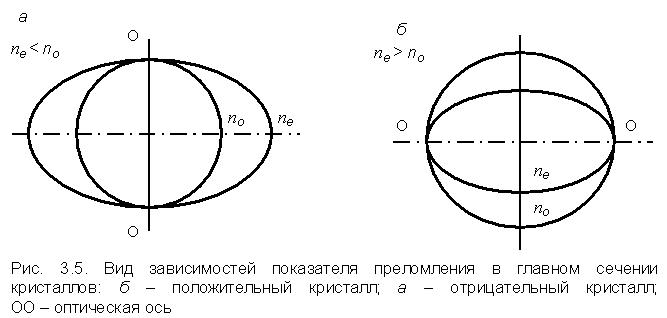
Различие показателей преломления обыкновенного и необыкновенного лучей и приводит к их пространственному разделению в кристалле.

Приборы, основанные на явлении двойного лучепреломления, называются поляризационными призмами.

    Однолучевые поляризационные призмы – призмы, дающие один линейно-поляризованный пучок лучей. В качестве примера таких призм на рис. 3.6, а приведена призма Николя (николь). Она представляет собой двойную призму из исландского шпата, склеенную вдоль линии АВ канадским бальзамом. Падающий на переднюю грань луч раздваивается на два луча – обыкновенный и необыкновенный. При соответствующем подборе угла падения, равного или больше предельного, обыкновенный луч испытывает полное внутреннее отражение (канадский бальзам для него является средой оптически менее плотной по сравнению с исландским шпатом). При этом преломление обыкновенного луча во вторую призму не происходит, и он поглощается зачерненной поверхностью СВ. Необыкновенный луч выходит из кристалла параллельно падающему лучу.

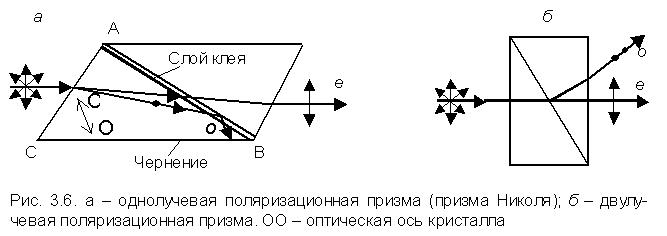
    Двулучевые поляризационные призмы – призмы, дающие два пучка лучей, поляризованных во взаимно-перпендикулярных плоскостях. В них используется различие показателей преломления обыкновенного и необыкновенного лучей, чтобы развести их как можно дальше друг от друга (рис. 3.6, б).