Вопрос 11: «Цилиндрическая и сферическая системы координат в пространстве».
С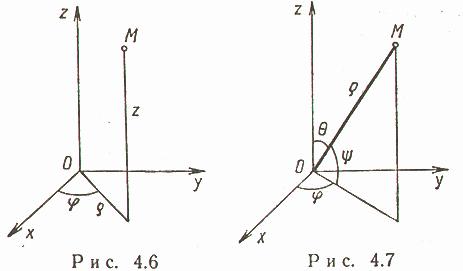
ферические
и цилиндрические координаты в пространстве.
Цилиндрические
координаты.
Главные значения
,
,
:
Связь между декартовыми
прямоугольными и цилиндрическими
координатами:
С
ферические
координаты.
Главные значения
,
,
θ:
Иногда вместо θ
рассматривают
:
Вопрос №12: «Скалярное произведение векторов и его свойства».
Скалярное произведение и его свойства.
Скалярным произведением
двух векторов называется число, равное
произведению длин этих векторов на
косинус угла между ними, т.е.
Из определения следует
где φ - угол между векторами.
В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевые значения.
Свойства скалярного произведения.
Вопрос №13: «Векторное произведение векторов и его свойства».
Векторным произведением
вектора
на вектор
называется третий вектор
,
определяемый следующим образом:
1) длина его равна
площади параллелограмма, построенного
на векторах
и
,
т.е.
где φ - угол между векторами
и
;
2) вектор
перпендикулярен векторам
и
;
3) векторы
после приведения к общему началу образуют
правую тройку векторов.
Свойства векторного произведения
Вопрос №14: «Смешанное произведение векторов и его свойства».
Смешанным произведением
трех векторов
называется число
Модуль смешанного произведения трех векторов численно равен объему параллелепипеда, построенного на этих векторах.
Свойства смешанного произведения:
Вопрос №15: Двойное векторное произведение».
Вопрос №16: «Уравнение прямой с угловым коэффициентом».
Вопрос №17: «Угол между прямыми. Условия параллельности и перпендикулярности двух прямых.
Определение.
Если заданы две прямые y = k1x
+ b1,
y = k2x
+ b2,
то острый угол между этими прямыми будет
определяться как
.
Две прямые параллельны, если k1
= k2.
Две прямые перпендикулярны, если k1
= -1/k2.
Теорема. Прямые Ах + Ву + С = 0 и А1х + В1у + С1 = 0 параллельны, когда пропорциональны коэффициенты А1 = lА, В1 = lВ. Если еще и С1 = lС, то прямые совпадают.
Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.
Вопрос №18: «Общее уравнение прямой».
Вопрос №19: «Общее уравнение плоскости. Нормальный вектор плоскости».
Вопрос №20: «Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей».
Вопрос №21: «Канонические уравнения прямой в пространстве».
Вопрос №22: «Угол между прямыми в пространстве. Условия параллельности и перпендикулярности двух плоскостей.
Вопрос №23: «Условие параллельности прямой и плоскости в пространстве».
Вопрос №24: « Условие перпендикулярности прямой и плоскости в пространстве».
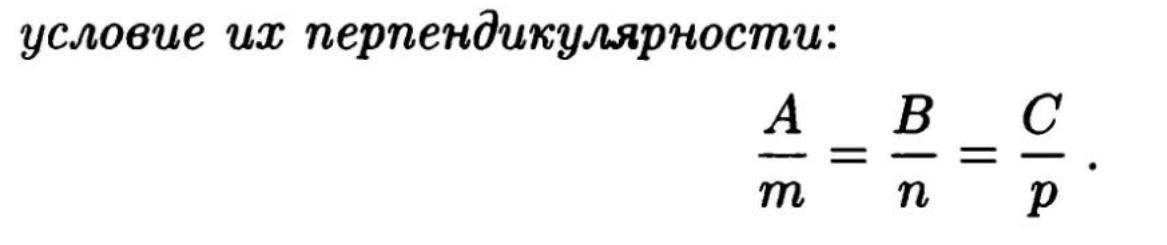
Вопрос №25: «Угол между прямой и плоскостью».
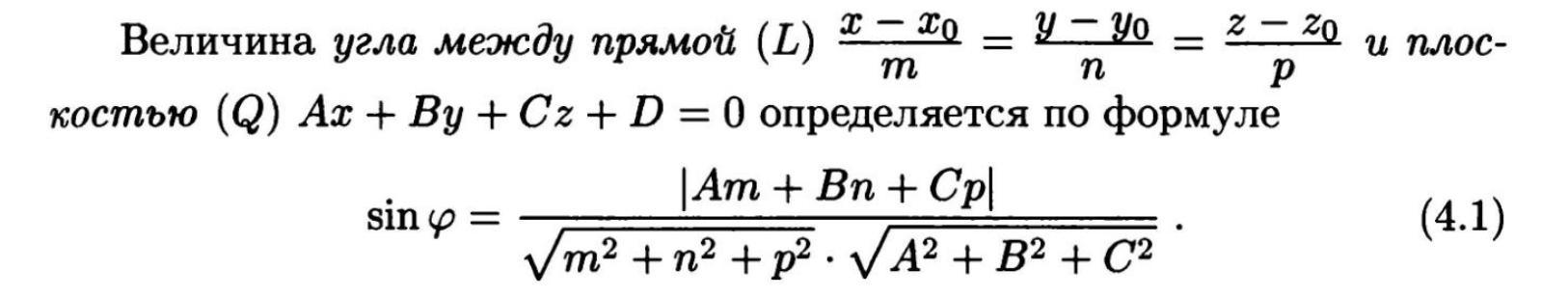
Вопрос №26: «Каноническое уравнение эллипса. Исследование формы эллипса».
Вопрос №27: «Каноническое уравнение гиперболы. Исследование формы гиперболы».
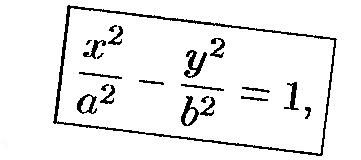
Вопрос №28: «Каноническое уравнение параболы. Исследование формы параболы».
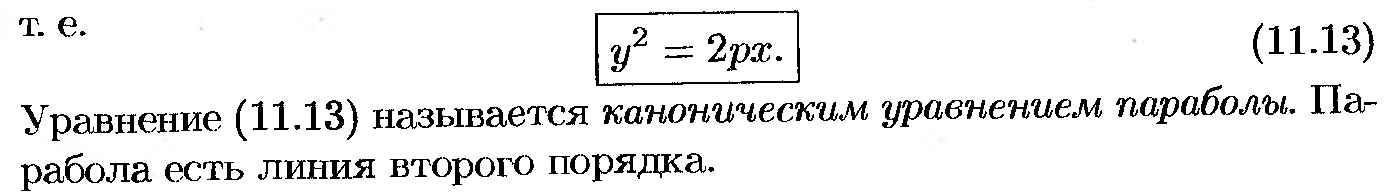
Вопрос №29: «Общее уравнение линии второго порядка. Понятие типа линии второго порядка».
Уравнение такого вида может определять: 1) эллипс (в частности, окружность), 2) гиперболу, 3) параболу, 4) пару прямых (параллельных, пересекающихся либо совпадающих), 5) точку или не определять никакой линии.
В простейшем случае, при В = 0, тип кривой можно определить, выделив полные квадраты переменных.
Вопрос №30: «Числовые последовательности и операции над ними, ограниченные и неограниченные последовательности».
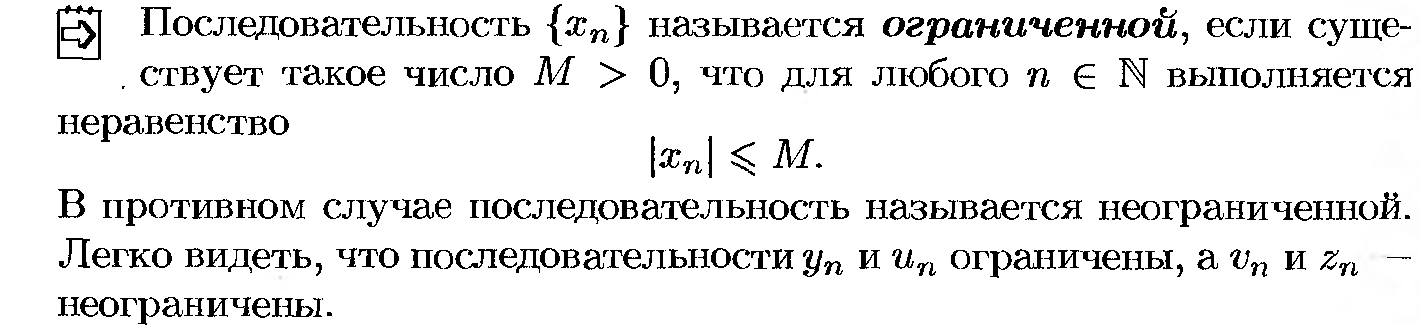
Вопрос №31: «Бесконечно большие и бесконечно малые последовательности, основные свойства бесконечно малых последовательностей».
Вопрос №32: «Сходящиеся последовательности: предел последовательности, основные свойства сходящихся последовательностей».
Вопрос №33: «Монотонные последовательности, число е».
Вопрос №34: «Определение функции. Способы задания функций».
Вопрос №35: «Предел функции. Односторонние пределы. Свойства пределов. Два замечательных предела».
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Односторонний предел числовой функции в точке — это специфический предел, подразумевающий, что аргумент функции приближается к указанной точке с определённой стороны (слева или справа). Числовая функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке совпадающие левый и правый пределы.
Вопрос №36: «Непрерывность и разрывы и функций».
Вопрос №37: «Обратные функции».
Пусть X и Y – некоторые множества и пусть задана функция f, т.е. множество пар чисел (x;y) (x ϵ X; y ϵ Y), в котором каждое число x входит в одну и только одну пару, а каждое число y – по крайней мере в одну пару. Если в каждой паре этого множества числа x и y поменять местами, то получим множество пар чисел (y;x), которое называется обратной функцией φ к функции f.
Вопрос №38: «Сложные функции».
Если на некотором множестве X определена функция z = φ(x) со множеством значений Z, а на множестве Z – функций y = f [φ(x)] называется сложной функцией от x [или суперпозицией (иногда композицией) функций φ(x) и f(z)], а переменная z – промежуточной переменной сложной функции.
Вопрос №39: «Производная. Ее физический и геометрический смысл».
Вопрос №40: «Правила дифференцирования».
Вопросы 41: «Производные от элементарных функций. Таблица производных».
Вопрос №42: «Дифференциал. Определение и геометрический смысл».
Вопрос №43: «Производные и дифференциалы высших порядков».
Вопрос №44: «Раскрытие неопределенностей. Правило Лопиталя».
Вопрос №45: «Формулы Тейлора и Маклорена».
Вопрос №46: «Разложение в ряд Маклорена элементарных функций, вычисление числа е».
