Интерференция волн.

В предыдущей лекции мы получили уравнение стоячей волны (4.34), описывающее колебания шнура (или иной среды), по которому навстречу друг другу распространяются две гармонические волны одинаковой частоты и амплитуды В результате наложения волн происходит перераспределение в пространстве объемной плотности энергии колебаний. В узлах, где волны встречаются в противофазе, эта энергия равна нулю. В пучностях, напротив, волны складываются в фазе, и энергия максимальна. Явление наложения волн, приводящее к перераспределению в пространстве объемной плотности энергии колебаний, носит название интерференции.

Интерференция является одним из фундаментальных явлений, присущих волнам различной природы (акустическим, электромагнитным, волнам на поверхности жидкости, плазменным волнам и др.). Она была хорошо известна еще во времена Ньютона, который осуществил замечательный опыт, приведший к открытию закономерностей интерференционной картины и получивший название "кольца Ньютона". Эти закономерности легко прослеживаются в опытах по интерференции капиллярных волн на поверхности жидкости. В следующей лекции дается описание характера движения частиц жидкости в таких волнах и устанавливается связь между частотой, длиной волны и скоростью ее распространения.

Один из таких опытов выглядит следующим образом (рис. 5.21). В неглубокую кювету К с большой площадью основания наливают воду. Волны на ее поверхности возбуждают с помощью вибратора В, приводящего в периодическое движение два маленьких шарика О₁ и О₂, которые являются точечными источниками волн. Эти шарики слегка погружены в воду и совершают синхронные колебания с частотой в направлении, перпендикулярном поверхности воды. От каждого из точечных источников распространяется волна с длиной и скоростью Гребни этих волн в фиксированный момент времени изображены на рисунке пунктиром. В результате наложения волн образуется интерференционная картина, которую удобно наблюдать в стробоскопическом освещении (освещая ее вспышками света, следующими также с частотой ). При таком освещении волны будут казаться практически неподвижными.

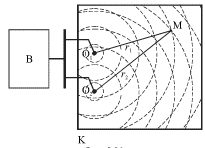Рис. 5.21.

Наиболее сильные возмущения поверхности будут наблюдаться в тех местах, где волны складываются в фазе. Говорят, что здесь располагаются интерференционные максимумы. В местах, куда волны приходят в противофазе, поверхность будет практически не возмущена: здесь располагаются интерференционные минимумы. Возмущение поверхности в произвольной точке M зависит от разности хода где и - расстояния от точки M до соответствующего точечного источника. Действительно, смещение s поверхности жидкости в точке M можно рассматривать как результат наложения двух синусоидальных (т.е. монохроматических) волн, прошедших расстояния и :

(5.44)

Здесь предполагается, что обе волны в точке M имеют одинаковые амплитуды (хотя это и не совсем верно), и постоянные фазовые добавки и так что их разность не зависит от времени.

Выполняя в (5.44) суммирование, получаем:

(5.45)

Если положить для простоты то положение интерференционных максимумов определяется из условия

(5.46)

Поскольку то последнему условию соответствует разность хода

(5.47)

где

Каждому максимуму принято присваивать порядковый номер, определяемый соответствующим числом (максимум нулевого, первого, минус первого и т.д. порядка). Интерференционные минимумы располагаются в тех местах, где

(5.48)

и так же нумеруются

Рассмотренная интерференционная картина соответствует идеализированной ситуации. Реальные волны даже в лучшем случае являются квазимонохроматическими. Для таких волн амплитуды и фазы и являются медленно меняющимися функциями времени (заметные изменения этих функций происходят за время ). Однако, если оба шарика приводятся в колебательное движение одним вибратором, разность фаз в (5.45) остается постоянной, положение интерференционных максимумов задается формулой (5.47) и не зависит от времени.

В практически важных случаях источники интерферирующих волн могут быть независимы. В нашем опыте это можно осуществить, если использовать два вибратора, к каждому из которых присоединен маленький шарик. Тогда разность фаз будет также изменяться на масштабе времени и ее можно записать в виде

(5.49)

где – среднее по времени значение разности фаз, - знакопеременная функция. Считая для простоты в (5.45) приходим к выводу, что интерференционная картина, как целое, будет достаточно хаотично смещаться в разные стороны. Если такую картину снимать на кинопленку со временем экспозиции кадра то на каждом кадре будет отпечатана усредненная за время "размазанная" картина. Она может стать совсем неразличимой, если интерференционные максимумы будут смещаться на величины, равные или превышающие расстояния между соседними максимумами. Такая ситуация достаточно часто встречается при интерференции световых волн. Чтобы полного "смазывания" картины не произошло, очевидно, необходимо выполнение следующего условия:

(5.50)

Чем лучше выполняется это неравенство, тем выше качество картины. Так, например, для световых волн и при визуальном наблюдении (для органов зрения ) мы всегда регистрируем "размазанную" интерференционную картину.

С качеством картины напрямую связано понятие когерентности интерферирующих волн. Когерентность характеризуется безразмерным коэффициентом (степенью когерентности), который может меняться в интервале Чем выше качество картины, тем больше степень когерентности. Для монохроматических волн, конечно,

Этим замечанием о когерентности волн мы здесь и ограничимся, а детальное описание этого понятия будет дано в курсе "Оптика".