32

1 Синтез кодовой комбинации циклического кода

1.1 Составление информационного блока

Необходимо составить информационный блок, состоящий из трех прописных букв – инициалов фамилии, имении отчества студента. Для составления необходимо использовать фрагмент кодовой таблицы первичного кода КОИ-8, который представлен на рис.1.

Старшие биты считываются из первых четырех строк, а младшие – из первых четырех столбцов, соответствующих месторасположению буквы на рисунке.

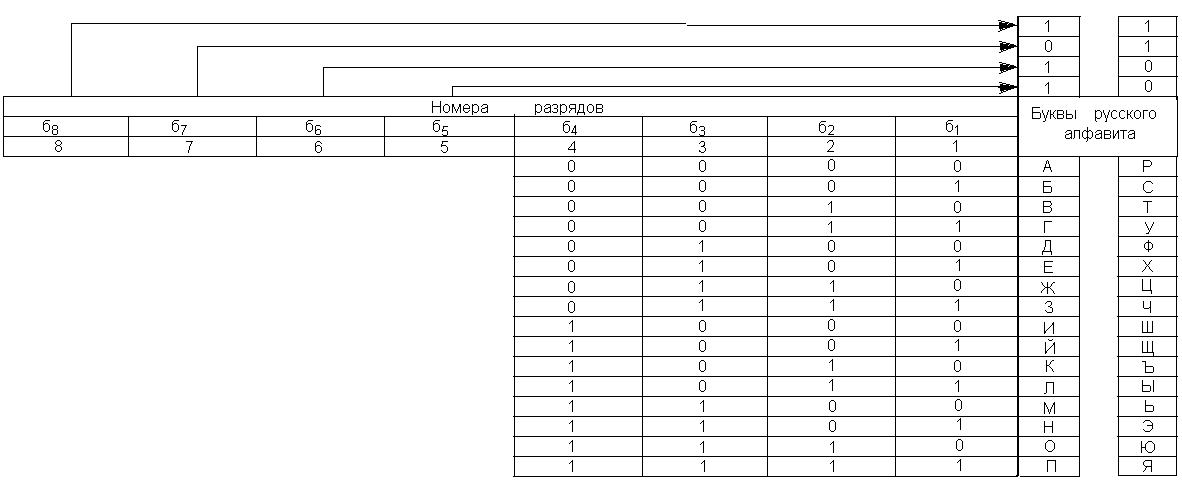
Рисунок 1.1 – Код КОИ-8. Фрагмент русского алфавита

Закодируем инициалы Колесник Сергей Владимирович:

Ч→1011 1010

К→1011 1000

А→1100 0001

1.2 Выбор образующего полинома циклического кода

Очевидно, что введение необходимой величины избыточности будет определяться длиной информационной части k, заданным значением допустимой вероятности ошибки 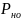, кратностью обнаруживаемых ошибок 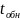и качеством самого канала связи.

Для инженерных расчетов широкое применение нашла модель потока ошибок, предложенная Л.П.Пуртовым, которая с достаточной для практики точностью описывает характеристики потока ошибок с пакетированием.

Исследую статистику ошибок в канале связи, было замечено, что вероятность появления ошибок кратности t в n разрядной кодовой комбинации равна:

;

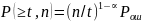где

Для канала без группирования (без памят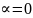и) , а при 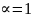ошибки сосредоточены в одном пакете.

Для обнаружения числа ошибок кратностью t необходим циклический код с кодовым расстоянием 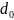не менее 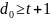тогда формула (1) примет вид:

.

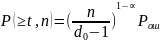С некоторым приближением можно связать вероятность появления ошибок кратности t [P( )] с вероятностью необнаруженной УЗО ошибки и числом проверочных разрядов в кодовой комбинации следующим образом:

и, выполнив преобразование, вычислим r

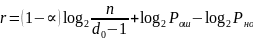
При расчете на ПКудобнее пользоваться десятичными логарифмами. После преобразований:

Так как в этой формуле n = k + r, требуемое значение r может быть определено путем подбора величины r, удовлетворяющее неравенству:

Зная величину r, т.е. величину высшей степени образующего полинома, следует выбрать соответствующий полином из таблицы 4.

Рассчитаем количество проверочных символов и выберем образующий полином для следующих исходных данных:

• Вероятность ошибки в канале связи

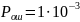
• Вероятность необнаруженной ошибки декодером

• Минимальное кодовое расстояние

• Коэффициент группирования

Подставим в формулу (6) исходные данные, а также значение r, начиная с 3:

r = 6 6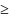 3,32[(1-0,5)log 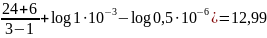– неравенство не выполняется

r = 1010 3,32[(1-0,5)log –

неравенство не выполняется

r = 14 14 3,32[(1-0,5)log –

неравенство выполняется. Поэтому, значение r = 14. Для выбора образующего

полинома из таблицы 4 справочного материала для выполнения курсовой работы

можно воспользоваться любым из трех приведенных полиномов для количества

проверочных символов, равного14. Выберем полином: .

1.3 Синтез кодовой комбинации циклического кода

Кодовая комбинация циклического кода может быть получена двумя способами. Первый получается умножением информационной последовательности на образующий полином P(x), что приводит к формированию неразделимого циклического кода. Неразделимость значительно усложняет процесс декодирования, поэтому на практике чаще используют второй способ, при котором информационная последовательность умножается на одночлен 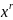и добавляется остаток от деления полученной последовательности на образующий полином. Это можно записать в виде формулы:

F(x) =

где F(x) – кодовая комбинация циклического кода;

G(x) – информационная последовательность в полиномиальной форме;

R(x) = 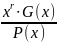– остаток от деления на образующий полином.

Для перевода двоичной последовательности в полиномиальную форму каждый бит умножается на x в степени, соответствующей месторасположению этого бита.

Приведем нашу последовательность, полученную в п. 1.1 в полиномиальную форму.

Ч									К									А
1	0	1	1	1	0	1	0	1		0	1	1	1	0	0	0	1		1	0	0	0	0	0	1

Полученную кодовую комбинацию можно записать как:

G(x) = +

Умножим G(x) на одночлен . Так как количество проверочных разрядов, рассчитанное в п. 1.2 равно семи, то умножаем на .

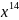G(x) = +

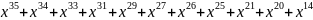
Для получения разрешенной комбинации циклического кода разделим полученную последовательность на выбранный в п. 1.2 образующий полином. Процесс деления показан ниже.

+

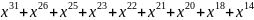
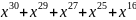
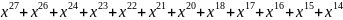
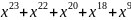
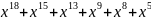
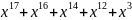
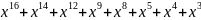
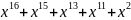
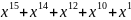
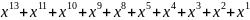= R(x)

Итак, разрешенная комбинация циклического кода, в соответствии с формулой (7) имеет вид:

F(x) = +

Переведем ее в двоичный вид:

1011101010111000110000011011110011111