Тренировочные задания по теме 2

1. Составить уравнение прямой, проходящей через точку М(-2;5)

параллельно прямой 5х-7у-4=0.

Ответ: 5х-7у+45=0.

2. Составить уравнение прямой, проходящей через точку М(4;5) перпендикулярно к прямой .

Ответ: .

3. Составить уравнение прямой, проходящей через точки А(1;5) и В(3;9).

Ответ: .

4. Даны вершины треугольника А(-1; 4), B (1; 5), C (6; 2) .

Определить:

а) длину стороны АВ;

б) высоту треугольника, опущенную из точки А на сторону ВС;

с) медиану АF, соединяющую вершину А с серединой стороны ВС;

с) угол между сторонами АВ и ВС;

д) площадь треугольника АВС.

Выполнить самостоятельно.

5. Упростить уравнение кривой , установить ее вид.

Ответ: гипербола, каноническое уравнение которой .

6. Упростить уравнение и определить вид кривой второго порядка: .

Ответ: парабола, каноническое уравнение которой .

0. Контрольные вопросы по теме 2

1. Уравнения прямой на плоскости.

2. Взаимодействие двух прямых линий.

3. Уравнение прямой, проходящей через заданную точку по заданному направлению

4. Уравнение прямой в отрезках.

5. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых.

6. Общее уравнение кривой второго порядка на плоскости.

7. Канонические уравнения окружности, эллипса. Гиперболы и параболы.

8. Преобразование уравнения кривой второго порядка и приведение его к каноническому виду.

Литература. А: 1-6; В: 9-9

3. Основные понятия теории множеств Определения , термины, символы

Множество- совокупности различных между собой объектов, объединяемых в целое некоторым общим признаком. Например, множество книг, чисел, студентов и т.п.

Обозначения: А,В.С…. – множества; а, b,c… - элементы (точки) множеств.

Изображение:

Круги или диаграммы Эйлера-Венна

.

Принадлежность:

принадлежит множеству S (входит в S);

не принадлежит множеству S (не входит в S).

Задание: два основных способа:

1. Перечисление: А={2; 5,6; 8}; В={b₁; b₂; b₃ ;…;b₉}; С={1; 3;… 2n-1};

2. Указание характеристического свойства: А={х|P(x)} – множество А состоит из элементов х, удовлетворяющих свойству P(x). Например, А состоит из точек интервала 1< х ≤ 2, то запишем: А={х|1< х ≤ 2}.

Задание множеств с помощью свойств используется при невозможности задать его перечислением.

При рассмотрении множества могут выделяться его отдельные части (например, по какому-либо фактору). Это называется выделением подмножеств:

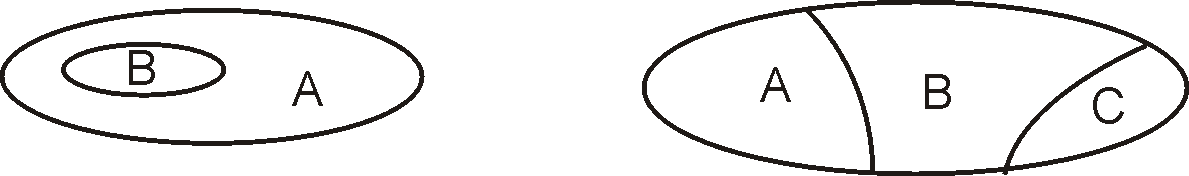
Множество В называется подмножеством множества А, если все элементы В принадлежат и А: В А – В включено (или содержится) в А. Если хотя бы один элемент В не содержится в А, то В А – В не подмножество (не включено в) А.

В А; С А;

D А; Е А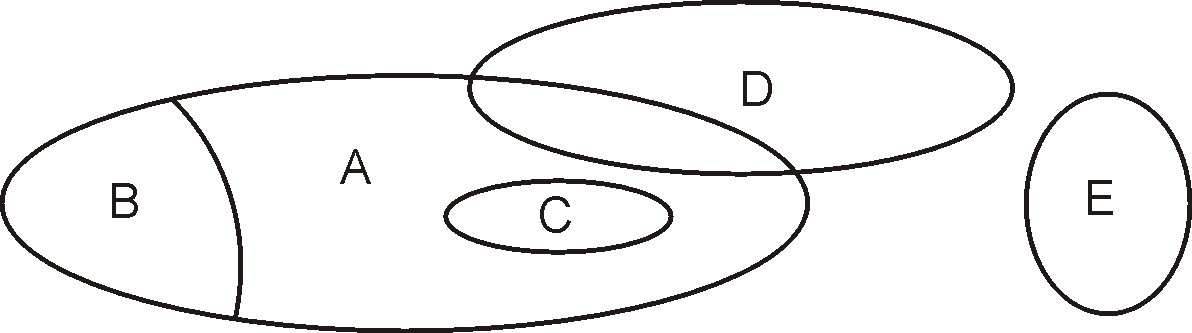

Множество, не содержащее ни одного элемента, называется пустым, обозначается символом Ø и аналогично понятию нуля в арифметике. Оно является подмножеством любого множества. Вообще, множество можно разбить на подмножества самыми различными способами. Так, из А={2; 12} можно получить подмножества: Ø , {2}, {12}, { 2; 12}. При этом Ø и { 2; 12} называются несобственными подмножествами А, остальные – собственными подмножествами А.

Операции над множествами

1. Множества А и В равны, А=В, тогда и только тогда, когда А В и В А, т.е., состоят из одних и тех же элементов, причем порядок следования элементов не имеет значения: если А={2; 3; 5} и В= {3; 5; 2}, то А=В.

2. Пересечением множеств А и В называется множество С, состоящее из всех элементов, принадлежащих одновременно и А, и В: С= А В= { х |х А и х А}.

С = А В

С = А В = Ø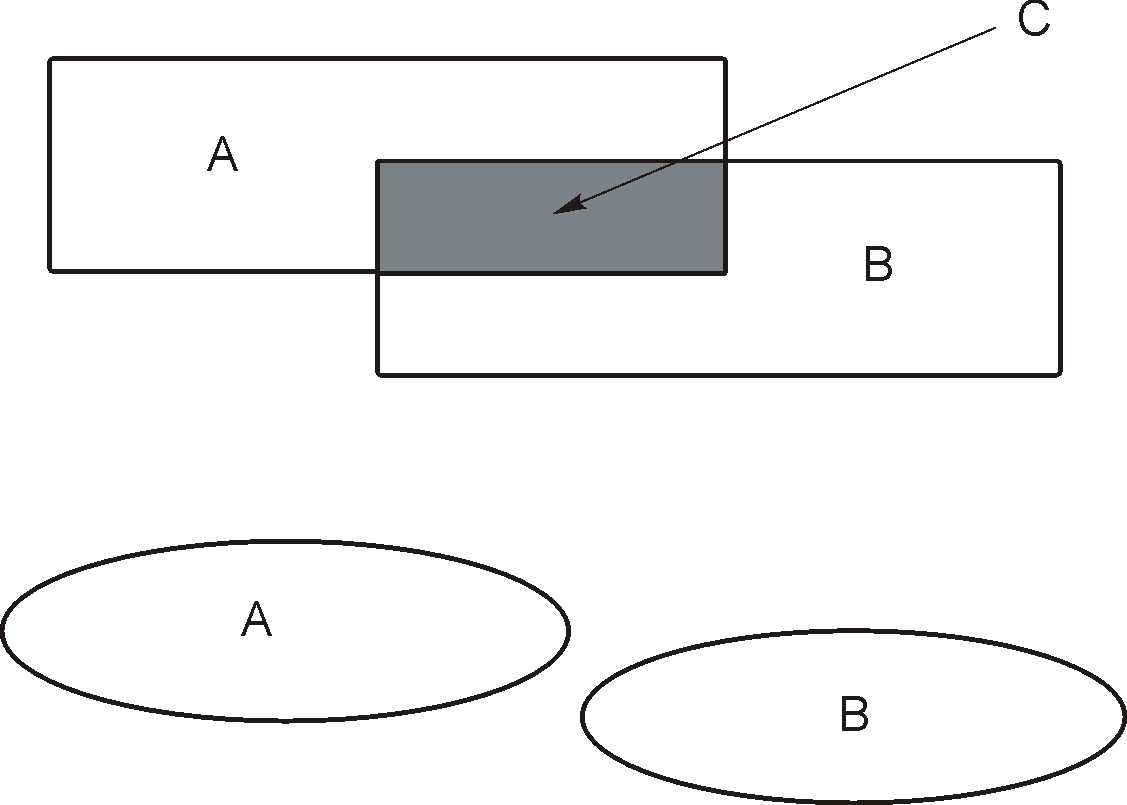

3. Объединением (суммой) множеств Аи В называется множество С всех элементов, входящих либо в А, либо в В. При этом общие элементы учитываются только один раз: С=А В = { х |х А или х А}.

С = А В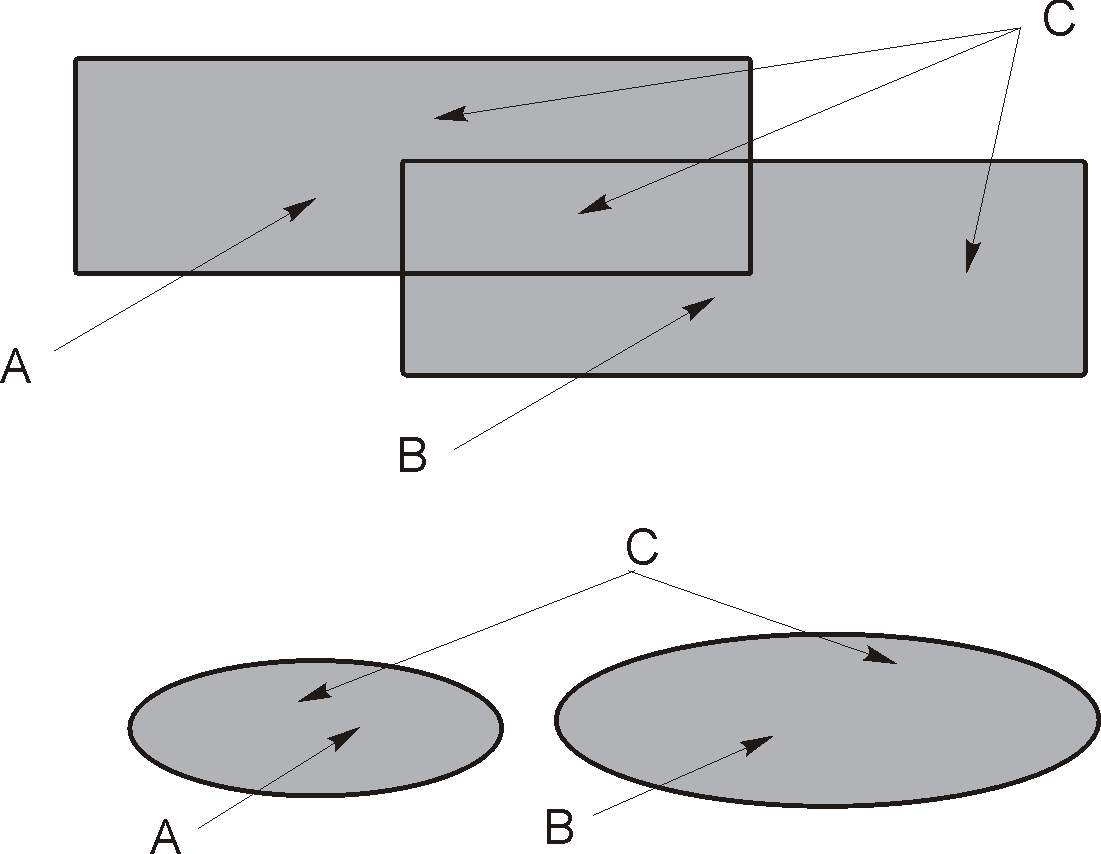

4. Разностью множеств А и В называется множество С, состоящее из тех элементов множества А, которые не содержатся в множестве В: С=А\ В = { х |х А и х А}.

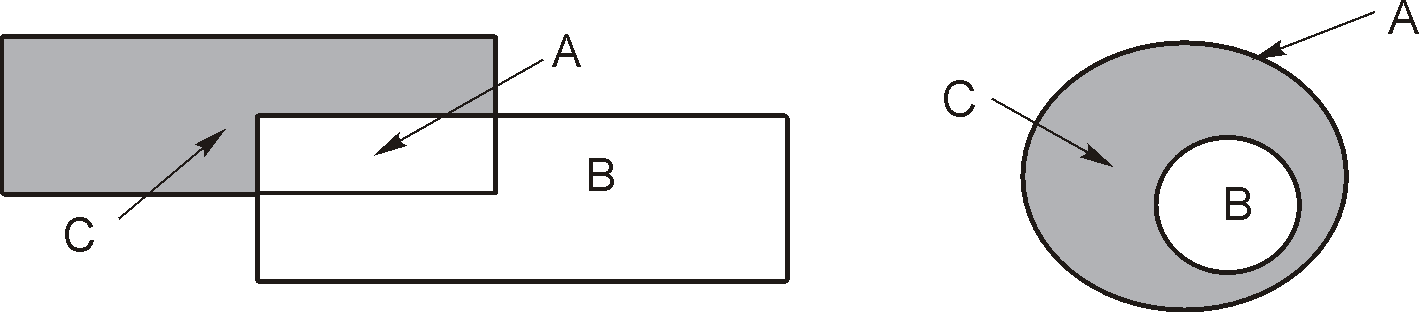
С=А\ В С_АВ =А\ В

Заметим, что на втором рисунке В А. В этом случае разность А\ В называется дополнением множества В до множества А и обозначается С_АВ =А\ В.

5. Симметрической разностью множеств А и В называется множество С, состоящее из элементов, принадлежащих только А и только В: С=А + В = (А\ В) (В\ А).

С = А + В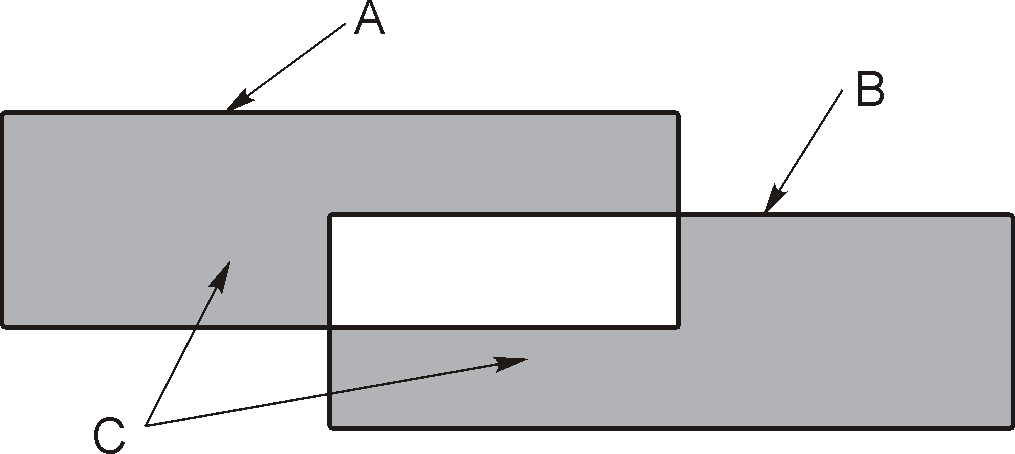

6. Абсолютным дополнением множества А называется множество всех элементов, которые не принадлежат множеству А. Например, если А = { х |х ≤ 2 }, то = { х |х > 2 }.

Введенные выше операции распространяются и на несколько множеств. С помощью диаграмм Эйлера можно легко доказать ряд свойств операций с множествами, во многом похожих на обычные арифметические. Наиболее часто встречаются следующие свойства:

1. А В = В А; А В = В А – коммутативность.

2. А (В С) – (А В) С; А (В С)= (А В) С – ассоциативность.

3. А (В С)=(А В) (А С); А (В С)=(А В) (А С) – дистрибутивность.

4. А Ø=А; А Ø = Ø.

5. А А=А; А А = А – идемпотентность.

6. А (А В) = А; А (А В)= А – поглощение.

7. А\ А = Ø.

8. А\ (А \ В)=А В.

9. С_Е(А В) = С_ЕА С_ЕВ ; С_Е(А В)= С_ЕА С_ЕВ – двойственность.