Практические задания по теме 2

Задание 1

Решить следующие задачи на тему «Прямая на плоскости».

1. Определить точку пересечения прямых 2х + 4у = 3 и у= х-1.

Система уравнений:

.

Решив систему, получим: х ≈ 1,17; у ≈ 0,17, что и является искомой точкой.

2. Составить уравнение прямой, проходящей через точку А(-2; 5) параллельно прямой 5х – 7у -4 = 0.

Приведем уравнение известной прямой к виду с угловым коэффициентов: . Из условий параллельности прямых искомая прямая будет иметь угловой коэффициент . Воспользовавшись уравнением прямой, проходящей через заданную точку с известным угловым коэффициентом, получим: . Отсюда 5 х – 7 у + 45=0.

3. Составить уравнение прямой, проходящей через точку А(4;5) перпендикулярно прямой .

Из условия перпендикулярности прямых: k₁·k₂ = -1 получим, . Тогда искомое уравнение будет: , отсюда у = 1,5 х -1.

4. Составим уравнение прямой, проходящей через две точки А(1;5)и В(3;9).

Воспользуемся уравнением прямой, проходящей через две заданные точки:

, т.е. . Отсюда: 2х – у + 3 = 0.

5. Даны вершины треугольника А(0; 4), B (-1; 2), C (10; - 4) .

О

пределить:

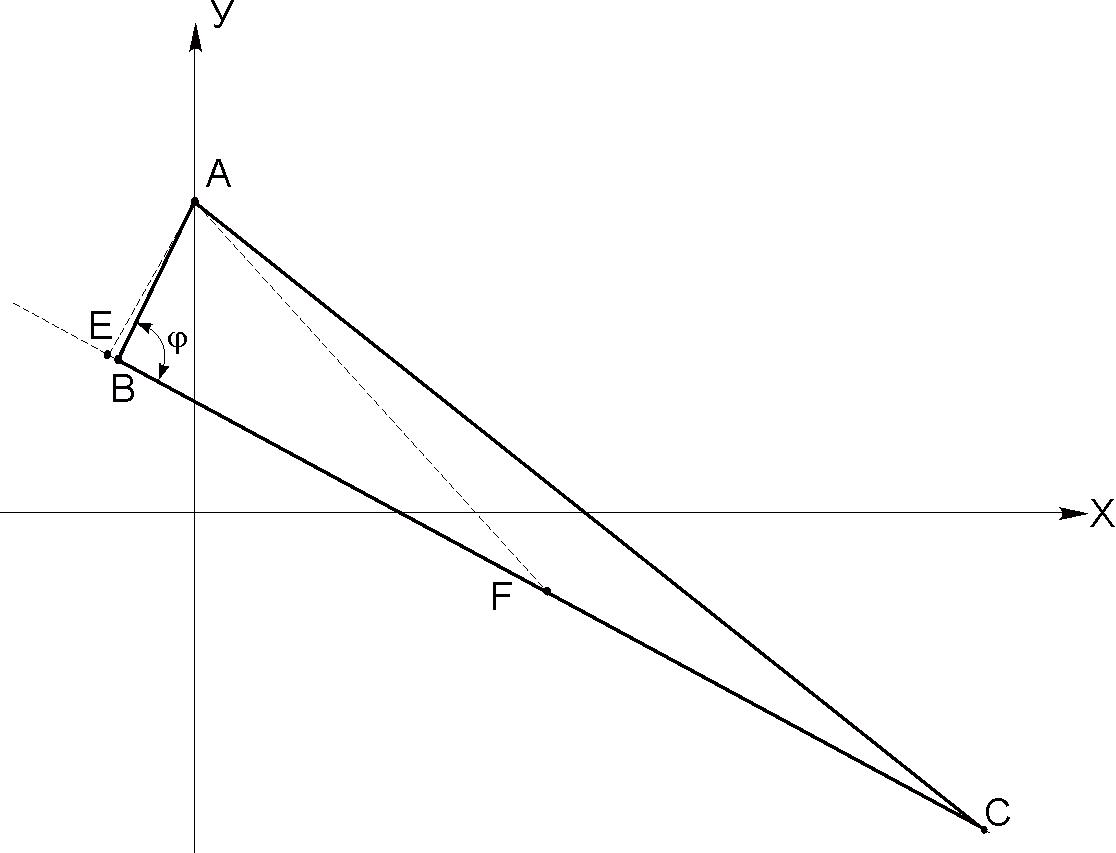
а) длину стороны АВ;

б) высоту треугольника, опущенную из точки А на сторону ВС;

с) медиану АF, соединяющую вершину А с серединой стороны ВС;

с) угол между сторонами АВ и ВС;

д) площадь треугольника АВС.

а) Находим длину стороны АВ (как длину отрезка).

AB= = =

б) Находим высоту треугольника (АЕ), опущенную из точки А на сторону ВС.

• Уравнение прямой ВС.

Воспользуемся уравнением прямой, проходящей через две заданные точки:

; Подставим значения точек В и С, получим:

, 6 (х-10) = -11(у+4), 6х -60 = -11у - 44, отсюда:

6х +11у -16=0 - общее уравнение прямой ВС.

Приведем уравнение к виду «с угловым коэффициентом»:

11у =- 6х +16, отсюда: у =- 6/11 х + 16/11, т.е. k_ВС = - 6/11.

• Условие перпендикулярности АЕ и ВС : k_АЕ k_ВС = -1. Следовательно, k_АЕ = 11/6.

Воспользуемся уравнением прямой, проходящей через заданную точку, с известным угловым коэффициентом : у – у₀ = k₀ (х- х₀). В нашем случае, прямая проходит через точку А(0,4) с угловым коэффициентом k_АЕ , т.е. ее уравнение: у – 4 = 11/6(х-0)  6у – 24 = 11х 

11х -6у +24 = 0 - уравнение высоты АЕ.

с) Найдем медиану АF, соединяющую вершину А с серединой стороны ВС.

• Находим координаты точки F ( середины отрезка ВС).

;

Таким образом, F (4,5; -1).

• Находим уравнение прямой АF. Для этого воспользуемся уравнением прямой, проходящей чрез две заданные точки:

. В нашем случае:

 5( х-4,5) = -4,5 (у+1)  5х –22,5 = -4,5 у -4,5  5х+4,5 у -18 = 0  10 х +9у -36 =0 - уравнение медианы АF.

д) Находим угол между сторонами АВ и ВС.

Зная уравнения сторон, можем вычислить tg угла между ними.

• Находим уравнение АВ, пользуясь уравнением прямой, проходящей чрез две заданные точки:

 2(х+1) = у-2  2 х + 2 = у – 2 .

Представим уравнение прямой АВ в виде «с угловым коэффициентом»: у = 2 х +4 , отсюда, k_вс = 2.

• Т.к. 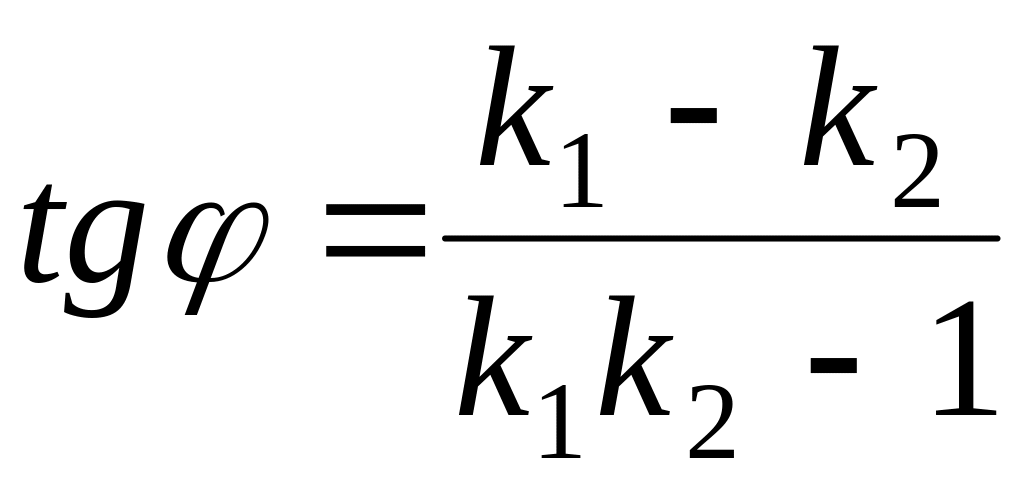- тангенс угла между прямыми с угловыми коэффициентами k₁ и k₂, то в нашем случае:

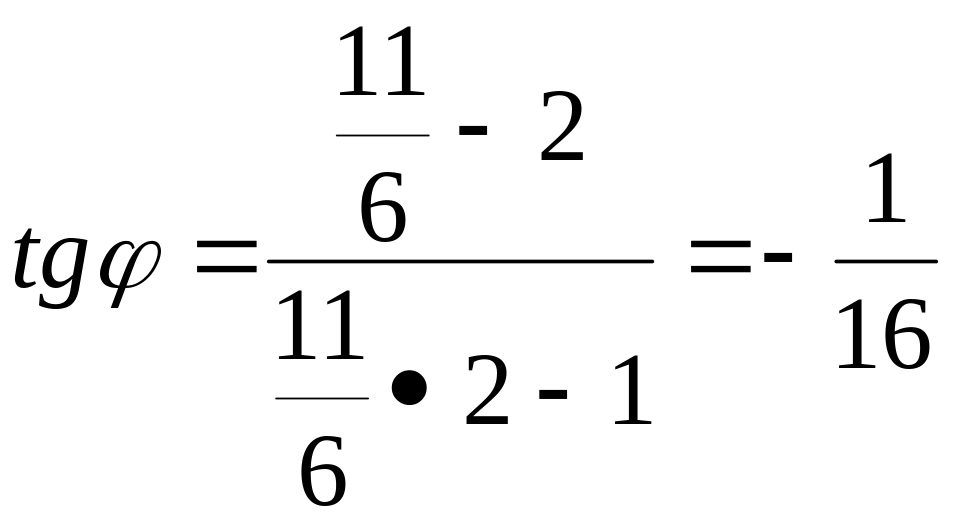, отсюда,  = arctg - ;  ≈ 93,6

е) площадь треугольника АВС вычислим по формуле:

; отсюда 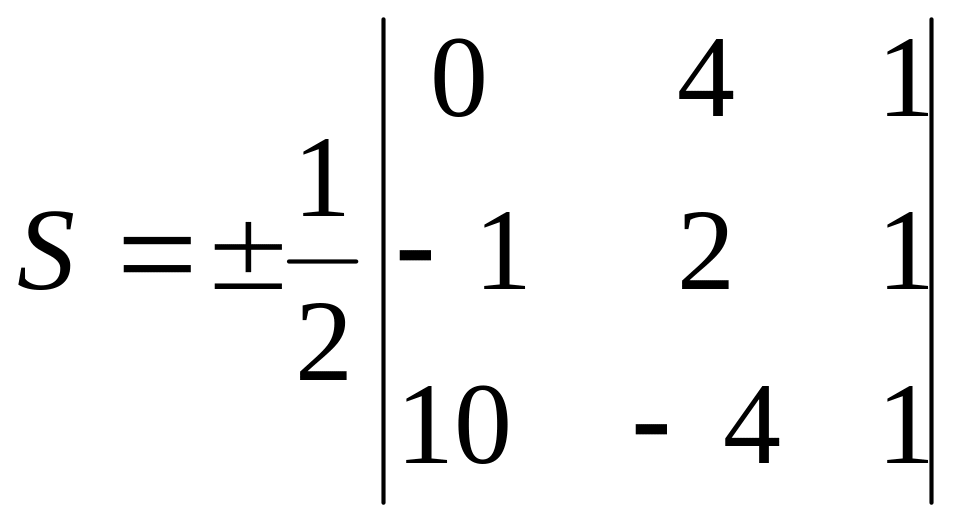=  0,5 (0 +40 +4 -20 +4 -0) = 14.

Задание 2

Решить следующую задачу на тему «кривые второго порядка на плоскости».

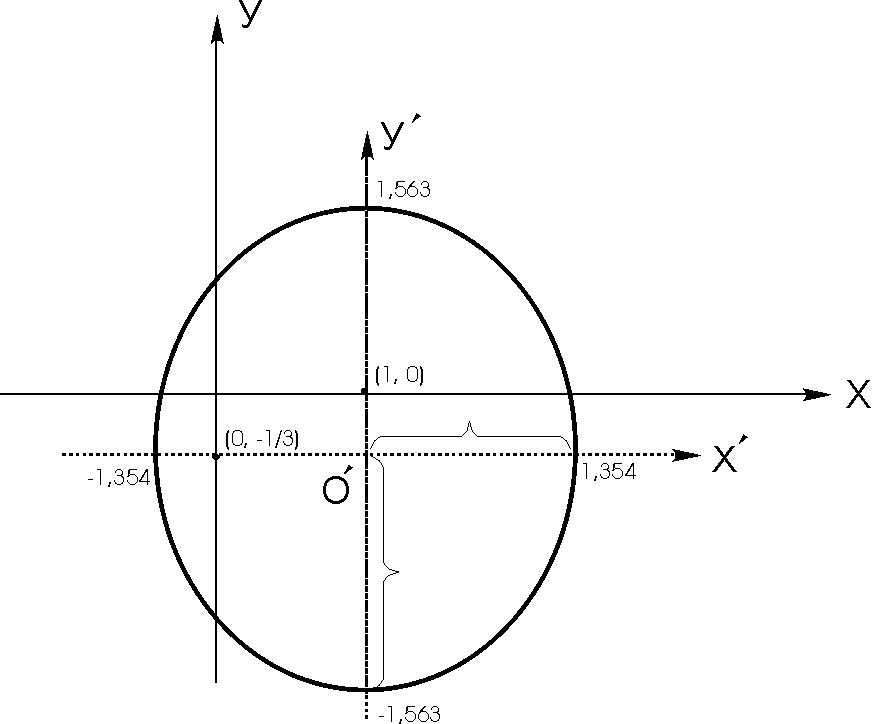
1. Определить тип кривой и построить на плоскости:

4х² +3y² -8 x + 2 y -3=0.

Т.к. коэффициенты при вторых степенях х и у не равны и имеют

один знак, представленная данным уравнением кривая – эллипс (рис. 2).

Сгруппируем в скобках элементы, содержащие х и у, следующим образом:

(4х² -8х) +(3у²+2у)-3=0  4(х² -2х) +3(у²+2/3 у) -3 = 0

Дополним каждую скобку до полного квадрата:

4(х² -2х+1)-4 +3(у²+2/3 у +1/9) -1/3 -3 = 0, т.е.

4(х -1)² +3(у +1/3)² =  4(х -1)² +3(у +1/3)² = 22/3.

Разделим обе части уравнения на 22/3:

, отсюда 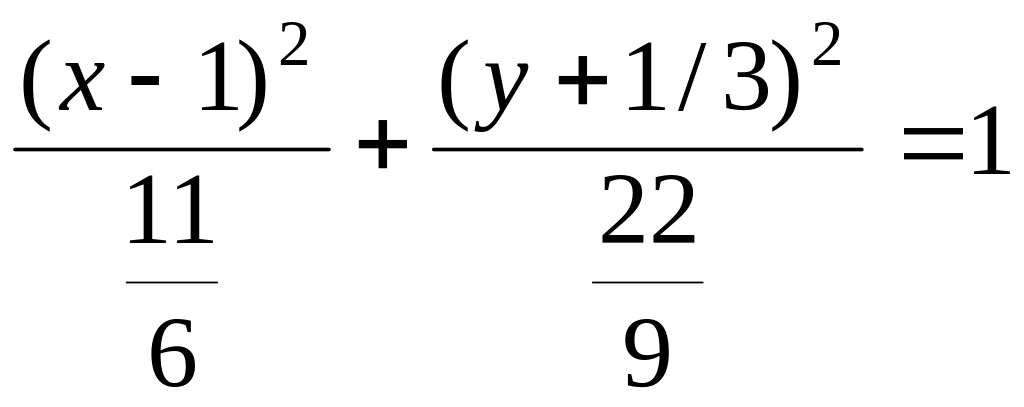, или .

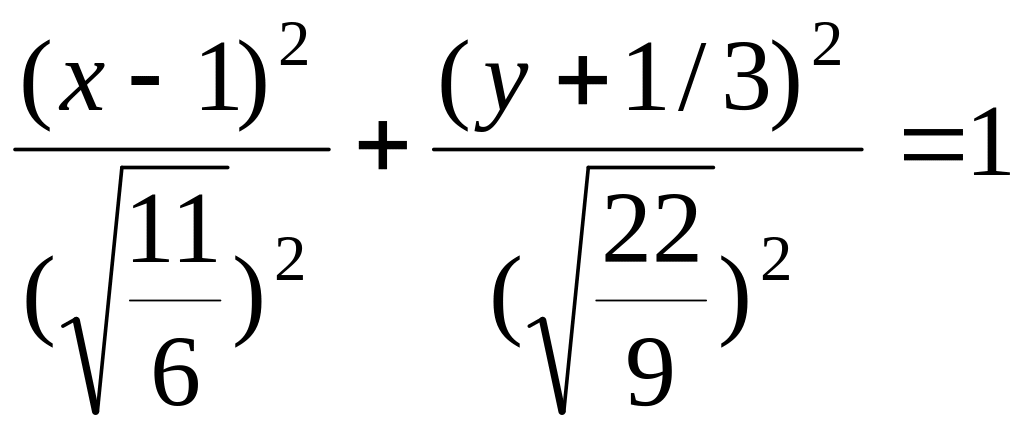Таким образом, заданное уравнение – уравнение эллипса с центров в точке О(1, -1/3) и полуосями:

а = ≈ 1,354,

b = ≈ 1,563.

На рисунке приведен эллипс, отвечающий полученному уравнению.