Тренеровочные задания по теме 1

1. Для матриц А= 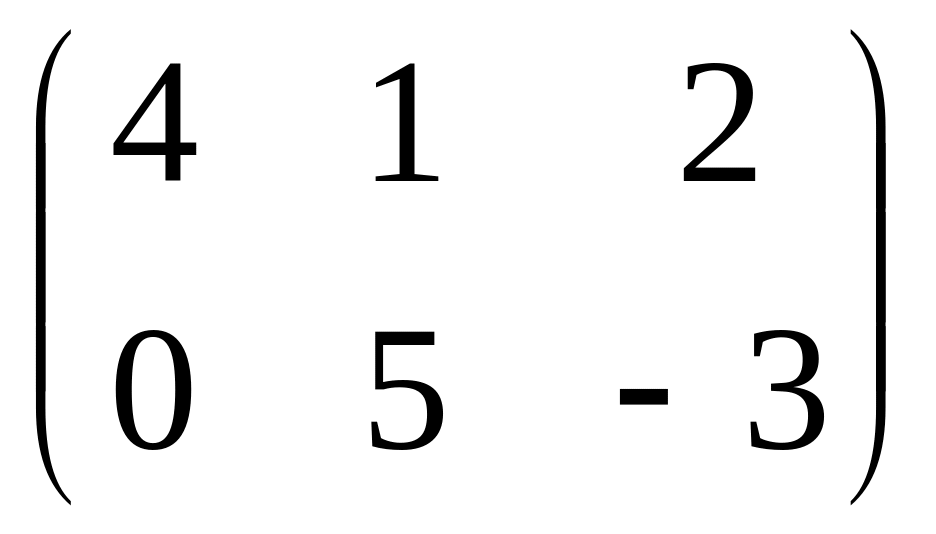и В=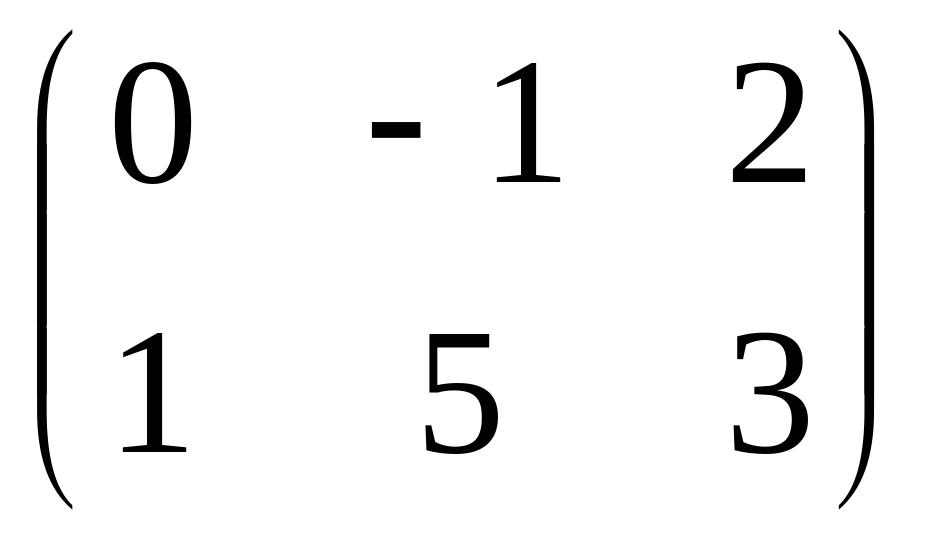 вычислить: С=4А-2В.

Ответ: С =

2. Протранспонировать матрицу А=

Ответ: А^T =

3. Вычислить определитель: det=

Ответ: Det=40

4. Вычислить А^-1 для матрицы А=

Ответ:

5. Найти ранг матрицы А=

Ответ: rang A=2

6. Решить системы линейных алгебраических уравнений:

а) методом Гаусса; б) матричным способом; в) по правилу Крамера.

I.

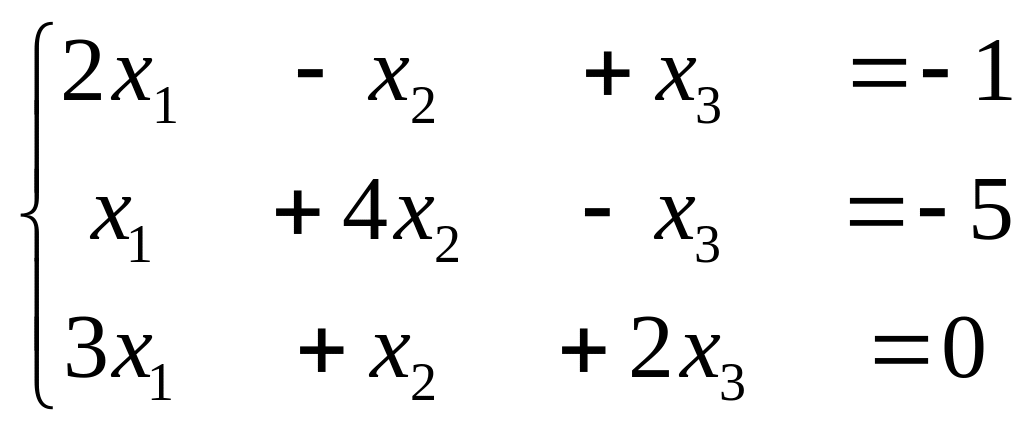
Ответ:

II.

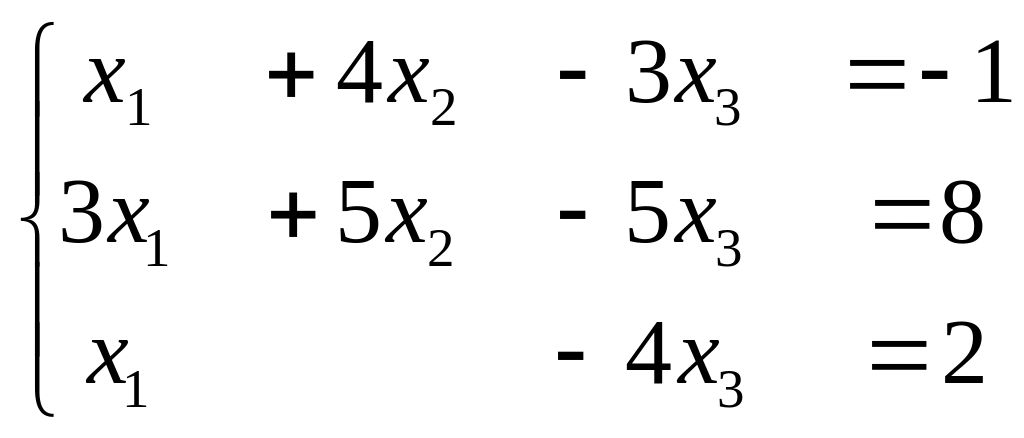
Ответ.

7. Исследовать СЛАУ на совместность:

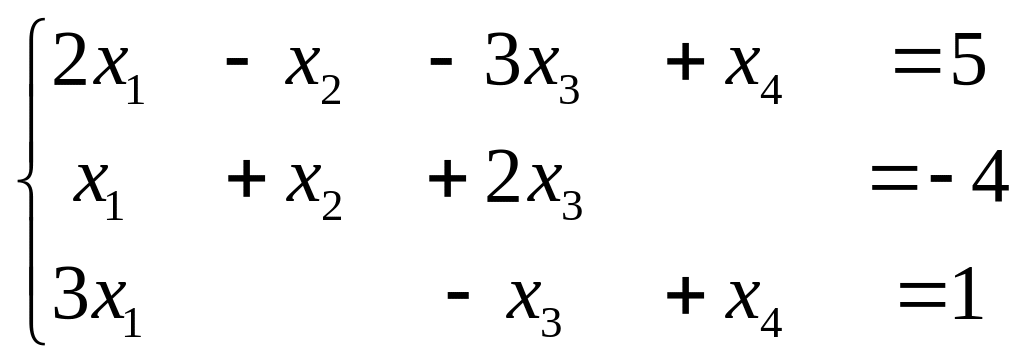
Ответ: Система совместна и неопределенна.

Контрольные вопросы по теме 1

1. Система линейных алгебраических уравнений (СЛАУ). Символика СЛАУ.

2. Определение матрицы. Виды матриц.

3. Сложение матриц. Умножение матрицы на число.

4. Умножение матриц.

5. Транспонирование матриц.

6. Присоединенная и обратная матрицы.

7. Определители второго порядка.

8. Определители третьего и n-ного порядка.

9. Основные свойства определителей.

10. Минор, адьюнкт.

11. Вычисление определителей третьего порядка.

12. Вычисление определителей методом разложения по строке.

13. Несовместность СЛАУ.

14. Решение СЛАУ методом Крамера.

15. Решение СЛАУ матричным методом.

16. Решение СЛАУ методом Гаусса.

Литература по теме 1. А: 1-6; Б: 11,2,7,9

2. Аналитическая геометрия

2.1. Прямая на плоскости

1. Длина отрезка, соединяющего точки А(х₁,у₁) и В(х₂,у₂):

AB =

2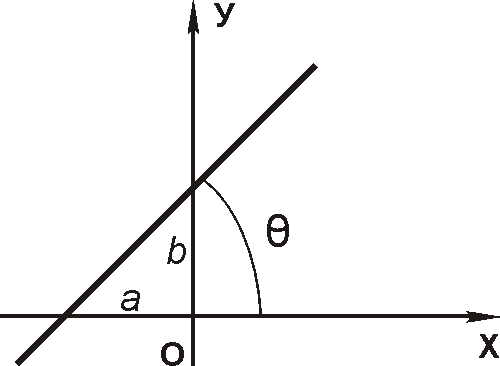 . Уравнение прямой с угловым коэффициентом: y=kх+b, где k = тангенс угла наклона прямой относительно оси ОХ, b – отрезок, отсекаемый прямой по оси ОУ.

3. Уравнение прямой в отрезках (каноническое уравнение прямой): , где а – отрезок отсекаемый прямой по оси ОХ, b – отрезок, отсекаемый прямой по оси ОУ.

4. Общее уравнение прямой на плоскости имеет вид Ах+Ву+С=0. Варианты общего уравнения:

А=0; Ву+С=0 или y= b – прямая, параллельная оси ОХ;

В=0; Ах+С=0 или х=const – прямая, параллельная оси ОУ;

С=0; Ах+Ву=0 или y=kх – прямая проходит через начало координат.

А=В=C=0 – вырождение прямой.

Всякое невырожденное уравнение первой степени Ах+Ву+С=0 при А²+В²≠0 является уравнением прямой линии на плоскости.

5. Угол β между прямыми А₁х+В₁у+С₁=0 (у=k₁x+b₁) и А₂х+В₂у+С₂=0 (у=k₂x+b₂) определяется из условия:

или ,

(здесь знак модуля обеспечивает положительный результат).

Отсюда:

- если прямые параллельны, то выполняется условие: k₁=k₂ ;

- если прямые перпендикулярны, соблюдается условие: k₁·k₂ =1.

7. Точка пересечения прямых определяется из системы уравнений:

8. Площадь треугольника, заданного своими вершинами А(х₁,у₁), В(х₂,у₂), С (х₃,у₃) определяется:

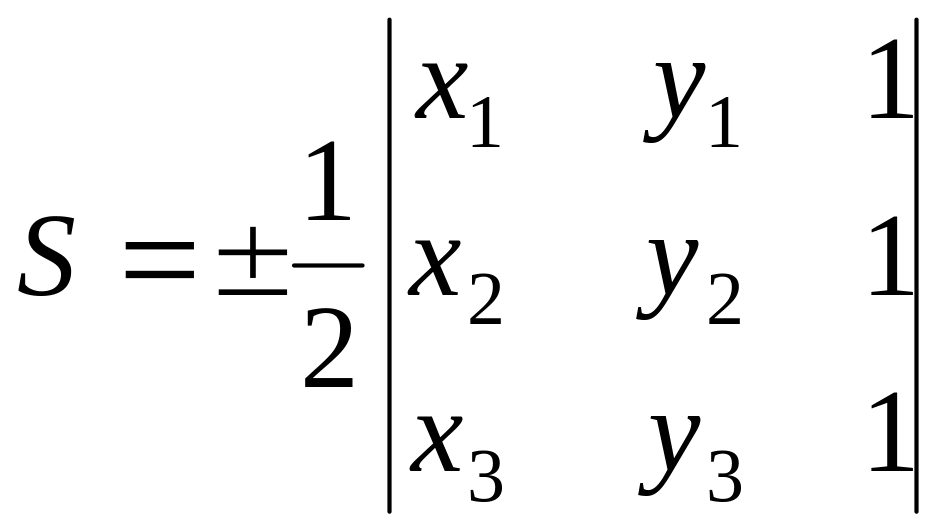
Варианты уравнения прямой.

У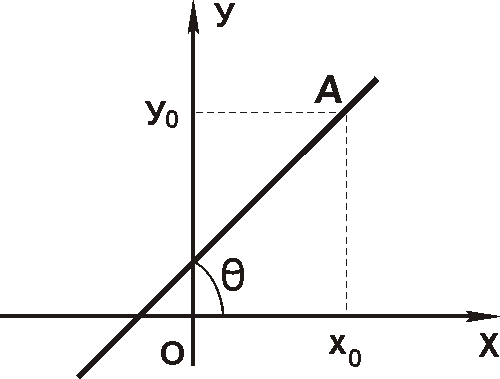 равнение прямой, проходящей через заданную точку А(х₀,у₀) и образующей угол θ с осью ОХ.

Т.к. θ известно, то k=tg θ. Тогда искомое

уравнение прямой:

у- у₀ = k(х- х₀)

2

. Уравнение прямой, проходящей через две заданные точки А(х₁,у₁) и В(х₂,у₂):
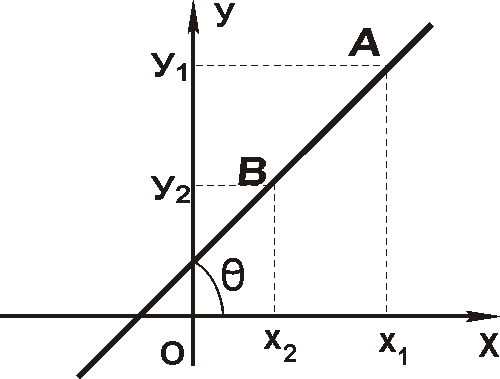