1.3. Определители

Понятие определителя вводится только для квадратной матрицы. Определитель – число, которое считается для квадратной матрицы по некоторым вполне определенным правилам. Порядок определителя – это порядок квадратной матрицы. В отличии от матрицы в символике определителей используются прямые скобки.

Определители второго порядка.

Пусть дана матрица А= . Тогда определитель второго порядка det A вычисляется по следующему правилу:

det A= = .

Определители третьего порядка.

Дана матрица А= 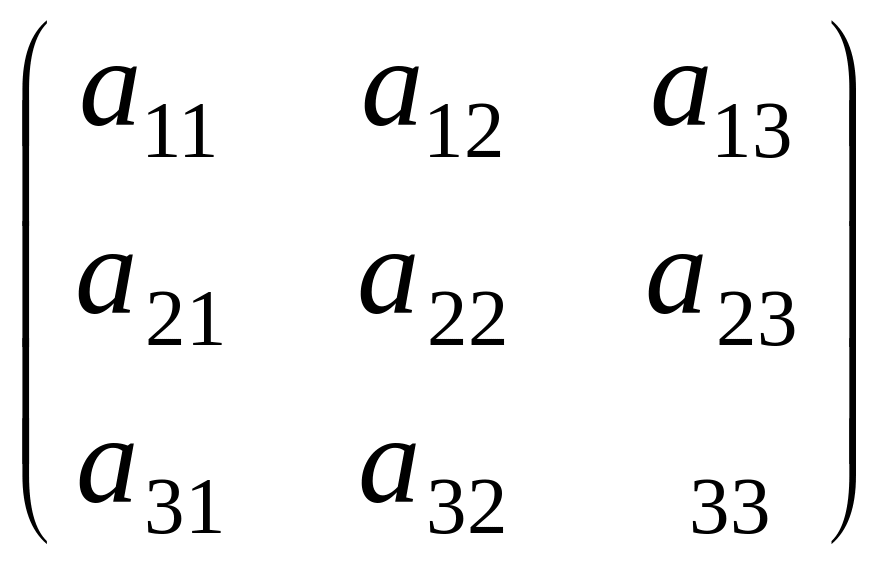. Тогда определитель третьего порядка det A вычисляется по формуле:

d

etA= =

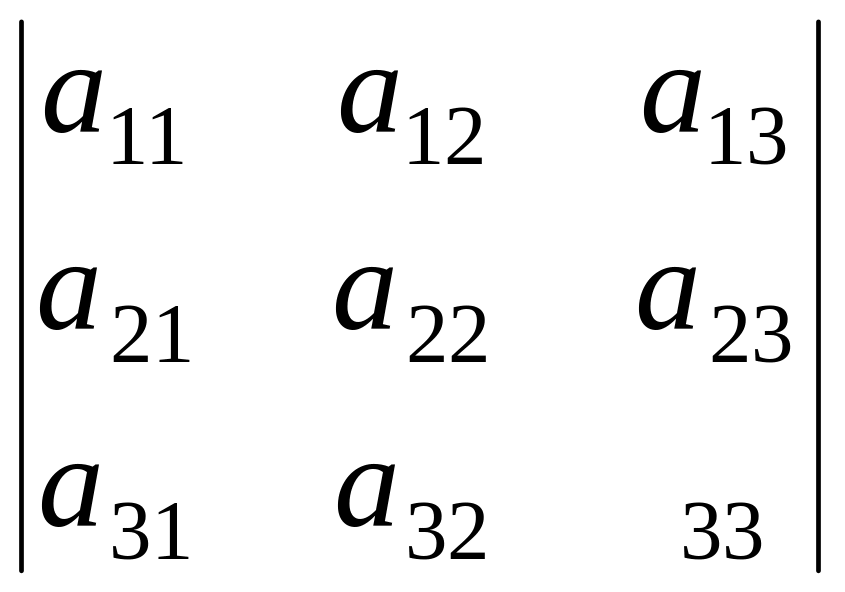Минором М_ij квадратной матрицы А называется определитель матрицы, полученный из матрицы А вычеркиванием i-той строки и j-того столбца.

Алгебраическое дополнение (или адьюнкт) . Здесь i – номер строки, j - номер столбца, где расположен элемент а_ij.

Вычисление определителя методом разложения по строке:

Определитель n-го порядка равен сумме произведений элементов строки или столбца на их алгебраические дополнения (адьюнкты), т.е.

det A= .

Здесь разложение определяется по i-той строке. Каждый элемент i-той строки умножается на свой алгебраическое дополнение. Полученные произведения складываются.

Свойства определителей

1. Определитель транспонированной матрицы равен определителю исходной матрицы, т.е. det = det А.

2. Определитель равен нулю, если:

- он содержит две одинаковые строки (столбца);

- он содержит нулевую строку (столбец);

- он содержит пропорциональные строки (столбцы).

3. Если поменять местами две строки (столбца) определитель изменит знак.

4. Общий множитель в строке (столбце) можно выносить за знак определителя.

5. Определитель не меняется, если к любой строке прибавить (из любой строки вычесть) любую другую строку, умноженную на любое число. Аналогичное свойство имеет место для столбцов.

1.4. Обратная матрица

Понятие обратной матрицы определено только для квадратных матриц, определитель которых не равен нулю (невырожденная матрица). Если D=0, то заданная матрица обратной не имеет и называется особенной (или вырожденной).

Матрица А^-1 называется обратной по отношению в матрице А, если выполняется равенство: А· А^-1 = А^-1· А = Е, где Е - единичная матрица. Порядок вычисления обратной матрицы следующий:

1. Вычисляет определитель D. Если D=0, матрица А – вырожденная и обратной не имеет.

2. Если D≠0, вычисляем все алгебраические элементы матрицы, т.е, все А_ij.

3. Из вычисленных алгебраических дополнений строим присоединенную (союзную) матрицу А^с, все индексы которой транспонированы по отношению к исходной матрице А.

4. Вычисляем .

Обратная матрица вычислена правильно, если выполняется условие А^-1· А = Е, где Е = единичная матрица.

0. Ранг матрицы

Определение 1. Система строк матрицы а₁, а₂,…а_n называется линейно независимой, если ни одна из строк не является линейной комбинацией других строк и линейно зависимой, если хотя бы одна строка является линейной комбинацией других строк.

Определение 2. Минором k-того порядка матрицы А называется определитель, образованный элементами, расположенными на пересечении каких-либо k строк и каких-либо k столбцов.

Определение 3. Число r называется рангом матрицы А (rang A), если:

1. существует хотя бы один минор порядка r матрицы, отличный от нуля;

2. все миноры (r+1) порядка равны нулю.

0. Решение систем линейных алгебраических уравнений

1. Правило Крамера решения СЛАУ

Необходимое условие решения СЛАУ по правилу Крамер: число уравнений равно числу неизвестных.

Достаточное условие: определитель, составленный из коэффициентов при неизвестных

det A ≠0. Тогда i-тое неизвестное вычисляется, как , где D = определитель, составленный из коэффициентов при неизвестных, D_i - тот же определитель, только вместо i-того столбца он содержит столбец свободных членов.

2. Матричный метод решения СЛАУ

Запишем систему линейных алгебраических уравнений в матричной форме: АХ=В. Если матрица А – невырожденная, то умножим обе части уравнения слева на обратную матрицу матрицы А: А^-1·АХ= А^-1·В. Т.к. А^-1· А = Е, то получаем ЕХ= А^-1·В. Т.к. ЕХ=Х, решение СЛАУ будет иметь вид:

Х= А^-1·В,

где Х – матрица неизвестных (столбец), А^-1 - обратная матрица матрицы А, В – матрица – столбец свободных членов.

3. Метод Гаусса решения СЛАУ(метод исключения

неизвестных)

Воспользуемся известными свойствами СЛАУ:

• СЛАУ эквивалентна исходной, если обе части одно уравнения умножить на одно и то же число;

• СЛАУ не меняется, если к элементам любого уравнения прибавить (или вычесть) соответствующие элементы другого уравнения, умноженные на любое число.

Пусть имеем систему n уравнений с n неизвестными. Выпишем расширенную матрицу системы:

.

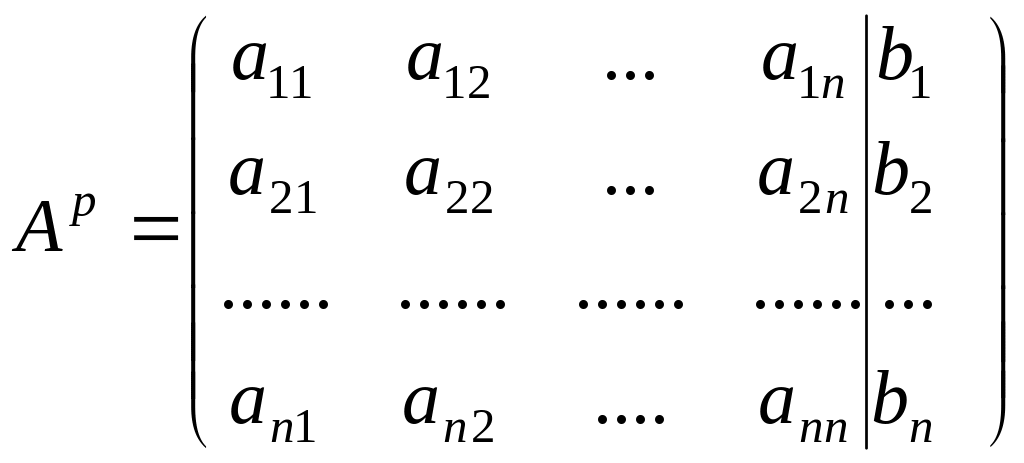Т.к. строки и столбцы матрицы состоят из коэффициентов СЛАУ, то для строк будут справедливы вышеописанные свойства системы. Воспользовавшись этими свойствами, приведем матрицу А к ступенчатому виду:

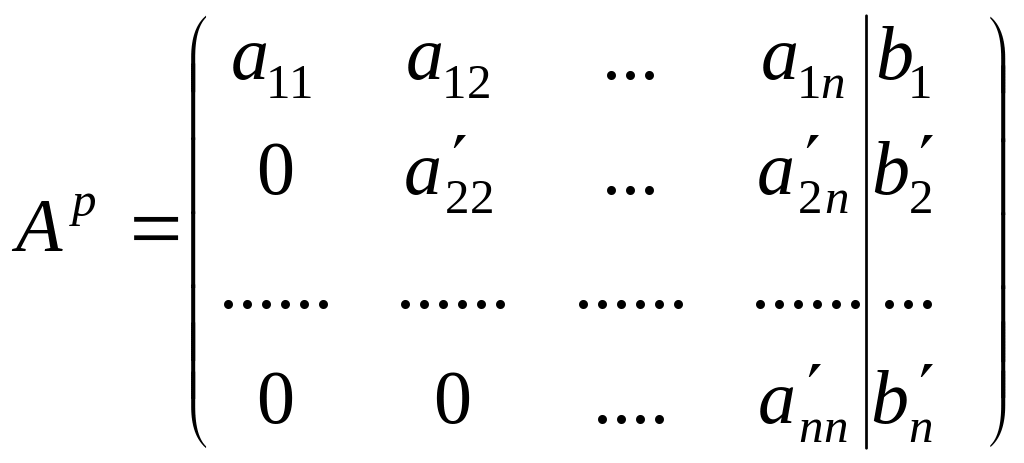
Реконструировав по коэффициентам систему, находим ее решение.