Тренировочные задания по теме 7

1. Построить полигоны частот и относительных частот по распределению выборки:

хi	2	4	7	8	9	12
ni	25	35	38	63	49	40

Рассчитать самостоятельно.

2. Построить гистограммы частот и относительных частот по распределению выборки:

№ интервала	Интервал длиной h=3	Сумма частот вариант ni
1	3 – 6	4
2	6 – 9	6
3	9 – 15	20
4	15 – 18	40
5	18 – 21	22
6	21 – 24	8
7	24 - 27	5

Рассчитать самостоятельно.

3. Для генеральной совокупности, заданной распределением

хi	20	25	30	35
ni	16	12	8	14

найти генеральную среднюю, дисперсию и стандарт.

Ответ. 27; 36; 6.

4. Для выборочной совокупности, заданной распределением

хi	2	4	7	8	9
ni	25	35	38	63	49

найти выборочное среднее, дисперсию, стандарт и исправленные оценки. Оценить моду, медиану и размах вариации.

Ответ. 10,67; 3,56 и 1,89; 3,62 и 1,90;

34; 12; 8.

Контрольные вопросы по теме 7

1. Задачи математической статистики.

2. Генеральная и выборочная совокупности.

3. Классификация выборок.

4. Варианты и вариационные ряды.

5. Полигон и гистограммы.

6. Генеральная и выборочная средние.

7. Генеральная и выборочная дисперсии и стандарты.

8. Несмещенные и смещенные оценки.

9. Эффективная и состоятельная оценки.

10. Исправление выборочной дисперсии.

11. Мода, медиана, размах и коэффициент вариации.

12. Статистическая гипотеза.

13. Статистический критерий проверки гипотез.

14. Последовательность проверки статистических гипотез.

Литература. А: 2, 3, 7,10; Б: 9,10.

КОНТРОЛЬНЫЕ РАБОТЫ

ТЕМЫ 1, 2

Вариант 1

1.Решить систему линейных уравнений:

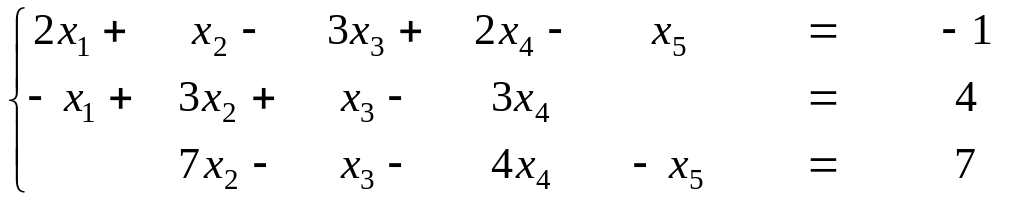
2. Доказать, что АА^-1=Е, если

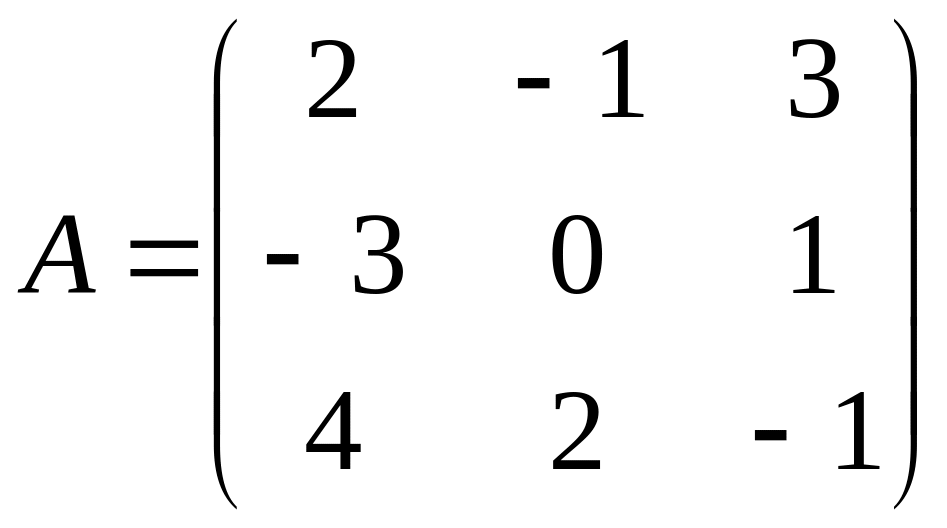
3. А(2,5), В(-3,6), С(0,4) – вершины треугольника. Составить уравнение сторон АВ и АС. Вычислить угол, образованный сторонами АВ и АС.

4. Какая линия задана уравнением: 2х²+4у²-12х+16у-48=0 ?. Написать каноническое уравнение кривой и построить на плоскости

Вариант 2

1.Решить систему линейных уравнений:

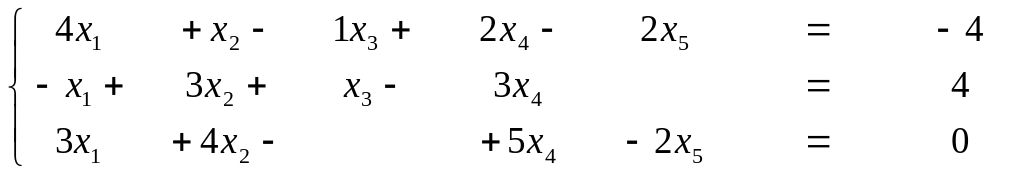
2. Доказать, что АА^-1=Е, если

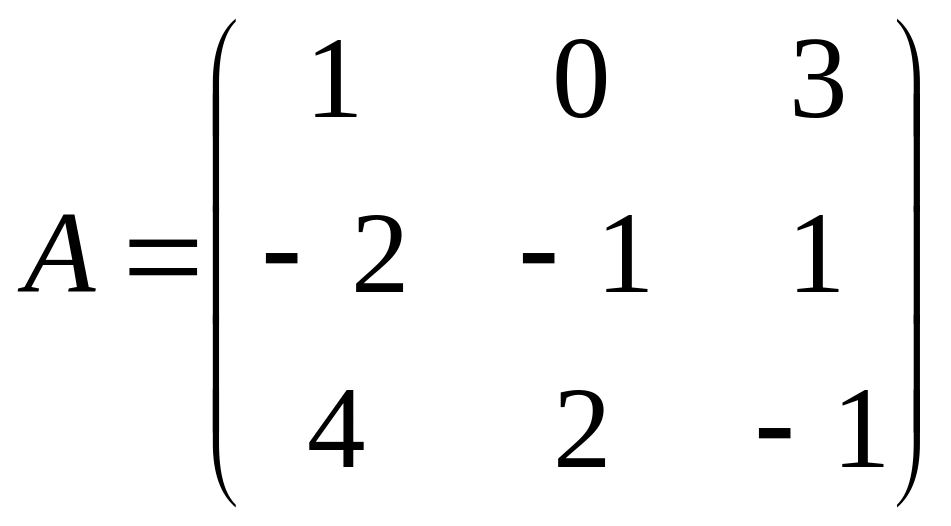
3. А(2,5), В(-3,6), С(0,4) – вершины треугольника. Составить уравнение стороны ВС и АС . Вычислить угол, образованный сторонами АС и ВС.

4. Какая линия задана уравнением: -2х²+6у²-12х+24у-16=0? Написать каноническое уравнение кривой и построить на плоскости

Вариант 3

1.Решить систему линейных уравнений по правилу Крамера:

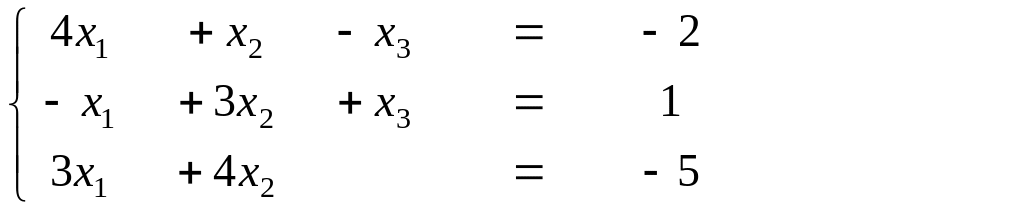
2. Вычислить АВ, если

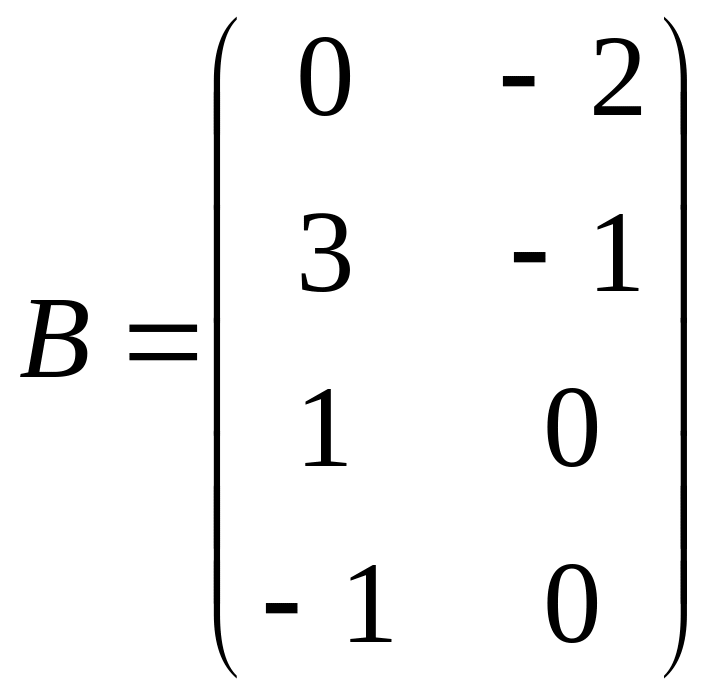
3. А(3,1), В(3,7), С(0,-4) – вершины треугольника. Найти точку пересечения медиан треугольника.

4. Какая линия задана уравнением: -2х²+6у²-12х+24у-16=0 ?

Вариант 4

1.Решить систему линейных уравнений методом Гаусса :

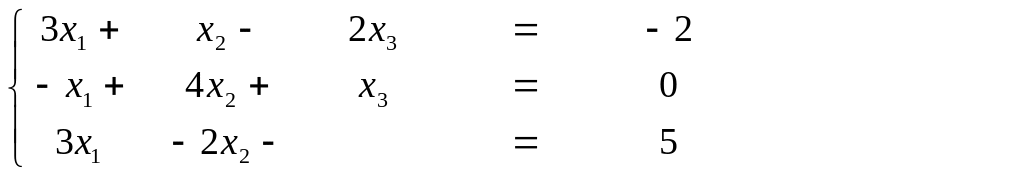
2. Вычислить АВ, если

3. А(3,1), В(3,7), С(0,-4) – вершины треугольника. Составить уравнения его сторон и прямой, соединяющей середины сторон АВ и АС.

4. Какая линия задана уравнением: 6у²-12х+24у-16=0

Вариант 5

1.Решить систему линейных уравнений матричным методом:

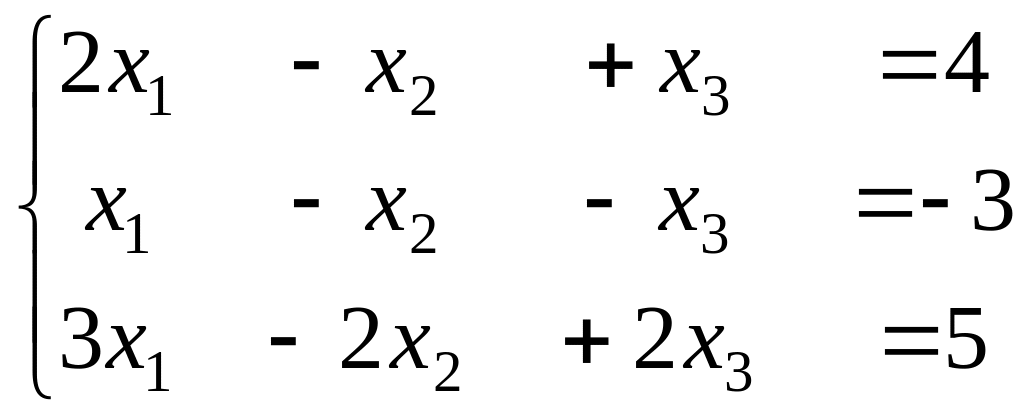
2. Вычислить определитель методом разложения по строке:

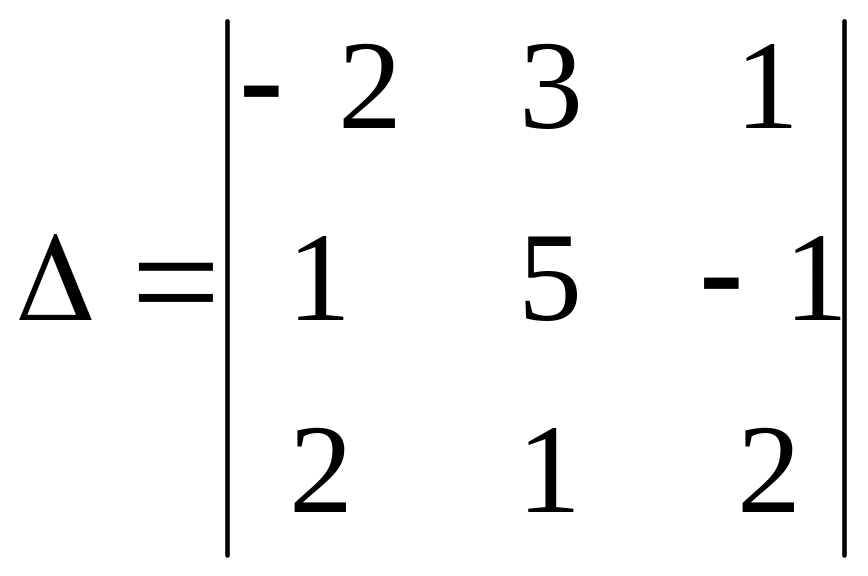
3. Даны вершины треугольника А(5,1), В(3,7), С(0,-4). Составить уравнение перпендикуляра, опущенного из вершины А на сторону ВС.

4. Какая линия задана уравнением: 3х²- 6у²-12х+24у-16=0

Вариант 6

1.Решить систему линейных уравнений методом Гаусса:

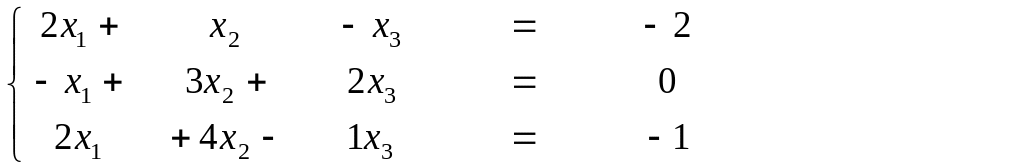
2.Найти ранг матрицы :

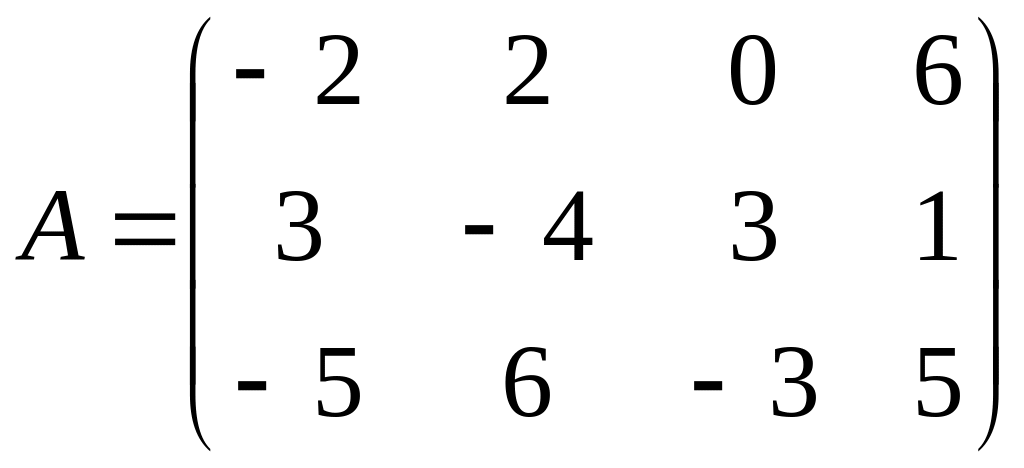
3. А(4,2), В(3,6), С(1,-4) – вершины треугольника. Найти уравнения его сторон.

4. Какая линия задана уравнением: 6у²-12х+24у-24=0 ?. Написать каноническое уравнение кривой и построить её на плоскости.

ТЕ МЫ 3, 4

Вариант 1

1. Найти область определения функции:

2. Исследовать интервалы монотонности функции:

3. Найти все первообразные функции:

Вариант 2

1. Найти область определения функции:

2. Найти точки экстремум функции:

3. Вычислить определенный интеграл:

Вариант 3

1. Вычислить предел:

2. Найти точки перегиба функции:

3. Вычислить определенный интеграл:

Вариант 4

1. Найти производную функции:

2. Вычислить предел:

3. Вычислить неопределенный интеграл:

Вариант 5

1. Найти область определения функции:

2. Найти точки экстремум функции:

3. Вычислить определенный интеграл:

Вариант 6

1. Вычислить предел:

2. Найти точки перегиба функции:

3. Найти все первообразные функции:

Вариант 7

1. Вычислить предел:

2. Вычислить производную функции:

3. Найти все первообразные функции:

Вариант 8

1. Вычислить предел:

2. Исследовать на экстремум функцию:

3. Вычислить неопределенный интеграл:

Вариант 9

1. Вычислить предел:

2. Найти производную функции:

3. Вычислить определенный интеграл:

Вариант 10

1. Вычислить предел:

2. Найти производную функции:

3. Вычислить:

Вариант 11

1. Найти функции:

2. Найти асимптоты кривой:

3. Вычислить:

Вариант 12

1. Вычислить предел, пользуясь правило Лопиталя:

2. Вычислить производную функции:

3. Вычислить площадь фигуры, ограниченной линиями: и у=1

Вариант 13

1. Найти функции:

2. Найти асимптоты кривой:

3. Вычислить площадь фигуры, ограниченной линиями: и осью Х

Вариант 14

1. Вычислить предел, пользуясь правило Лопиталя:

2. Вычислить производную функции:

3. Вычислить площадь фигуры, ограниченной линиями: и у=1

Вариант 15

1. Вычислить предел, пользуясь правило Лопиталя:

2. Исследовать на экстремум функции:

3. Вычислить площадь фигуры, ограниченной линиями: и у=9

ТЕ МА 6

1. Эксперимент состоит в m – кратном подбрасывании монеты. А₁, А₂,… А_m - случайные события – появления герба в первом, втором,… m – ном подбрасывании. Записать выражения для событий:

В – герб появится ровно 1 раз;

С – герб появится хотя бы 1 раз;

Д – герб не появится ни разу.

2. Лотерея содержит m + n +k билетом, из которых k выигрышных. Наудачу куплено r билетов. Вычислить вероятность событий:

А – два билета с выигрышем;

В – хотя бы один билет с выигрышем.

3.Поставка оборудования производится с трех предприятий. Первое осуществляет 30% оборудования, второе – 20%, третье – 50%. Появления брака в оборудовании на первом предприятии возможно с вероятностью 0,1m; на втором – 0,01 n, на третьем – 0,05k.

С какой вероятностью можно считать, что полученное бракованное оборудование выпущено вторым предприятием?

4. Проводится серия из n выстрелов по цели, вероятность попадания в которую р = 0,15.

Для поражения цели достаточно 1 попадания.

а) Найти вероятность того, что цель будет поражена.

б) Найти вероятность попадания в цель r раз.