Числовые характеристики дискретных случайных величин

I Математическим ожиданием дискретной случайной величины Х называется сумма произведений всех ее возможных значений ( ) на их вероятности ( , ,.. ):

.

Следует отметить, что математическое ожидание есть неслучайная величина, приближенно равная (и тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания:

- математическое ожидание постоянной равно самой постоянной: ;

- постоянный множитель можно вынести за знак математического ожидания: ;

- математическое ожидание произведения двух независимых случайных величин Х и Y равно произведению их математических ожиданий: ;

- математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: .

II. Дисперсия дискретной случайной величины.

Часто математического ожидания не достаточно для характеристики случайной величины и требуется информация о том, как они рассеяны вокруг среднего значения. Для этого вводятся и другие числовые характеристики.

Пусто Х – случайная величина с математическим ожиданием . Отклонением Х₀ назовём разность между случайной величиной и её математическим ожиданием: . Математическое ожидание отклонения . Отклонение является промежуточной характеристикой, на основе которой введем характеристику, называемую дисперсией.

Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины:

.

Свойства дисперсии:

- дисперсия постоянной величины равна нулю: ;

- постоянный множитель можно вынести за знак дисперсии: ;

- дисперсия суммы и разности двух случайных величин равно сумме дисперсий слагаемых: и .

Удобной вспомогательной характеристикой, используемой в расчетах чаще, чем дисперсия, является среднеквадратическое отклонение (или стандарт) случайной величины:

.

Пример:

Пусть случайная величина задается распределением:

Х	2	3	10
р	0,1	0,4	0,5

Вычислим математическое ожидание: =2·0,1+3·0,4+10·0,5=6,4.

2²·0,1+3²·0,4+10²·0,5= 54 ,

тогда = 54 - 6,4² =13,04.

.

Числовые характеристики непрерывных случайных величин

Математическим ожиданием непрерывной случайной величины Х Ю, возможные значения которой принадлежат интервалу , называют определенный интеграл:

.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата её отклонения:

.

Среднеквадратическое отклонение (или стандарт) непрерывной случайной величины:

.

Законы распределения непрерывных случайных величин

При решении задач, выдвигаемых практикой, приходится сталкиваться с различными распределениями непрерывных случайных величин. Плотности распределения случайных величин называют также законами распределения. Чаще всего встречаются законы равномерного, нормального и показательного распределений.

1. Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные случайные величины, плотность распределения сохраняет постоянное значение С: на интервале .

Н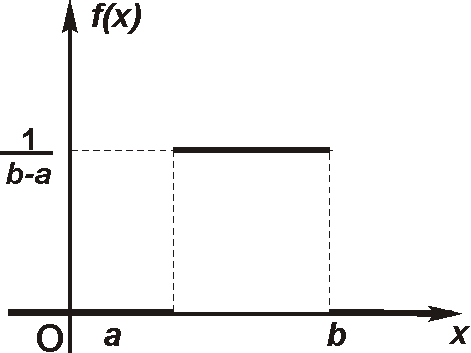 айдем постоянную С из свойства плотности распределения: , т.е. , откуда . Таким образом, плотность вероятности равномерного распределения: f(x)=0 при ; f(x)= при ; f(x)=0 при . График этой функции показан на рисунке.

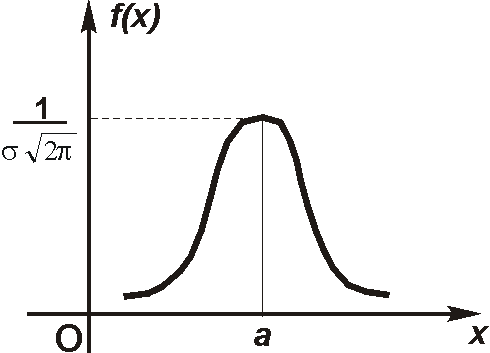6. Н ормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью:

.

Нормальное распределение5 определяется двумя параметрами: а и σ, где а – математическое ожидание, σ – среднее квадратическое отклонение нормального распределения. График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

Если случайная величина Х распределена по нормальному закону, то вероятность того, что Х примет значение, принадлежащее интервалу равна .

С помощью функции Лапласа , эта формула обычно записывается в виде:

.

Такое представление позволяет пользоваться готовыми таблицами, представленным в списке литературы.

6. Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью: при х < 0 и при х ≥ 0, где λ – постоянная положительная величина. Таким образом, показательное распределение определяется одним параметром. Такая особенность распределения указывает на его преимущество по сравнению с распределениями, зависящими от большого числа параметров. Интегрируя плотность распределения, находится функция распределения показательного закона. Вероятность попадания в интервал непрерывной случайной величины Х, которая распределена по показательному закону: . Значения функции находят по таблицам или с помощью калькулятора.

Х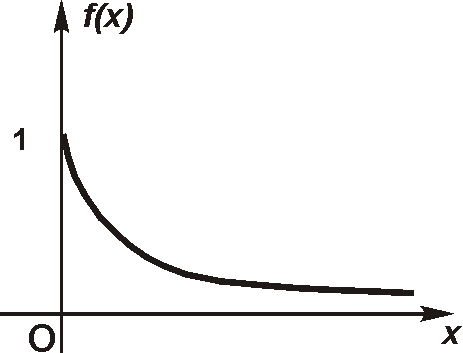 арактерной особенностью показательного распределения является равенство между собой математического ожидания и среднеквадратического отклонения: .